Module 6: Sets and lists
Supplemental material
Set operations: intersection, union, difference
What is a set?
- A set is merely a collection of items or objects.
- For example:
- A = {1, 3, 5, 7, 9} (odd numbers less than 10)
- B = {1, 2, 3, 5, 7} (primes less than 10)
- Standard operations on sets:
- Union: the union of A and B is
the set consisting of elements found in either:
⇒
A union B = {1, 2, 3, 5, 7, 9}
- Intersection: those elements in both sets
⇒
A intersection B = {1, 3, 5, 7}
- Difference: elements found in one but not in the other
⇒
A - B = {9}
List data structures as sets:
- We will use a list data structure to hold the elements of a set.
⇒
We'll use the LinkedList data structure already in the Java library.
- In our example, we'll store String's as elements.
Here's the example:
// We need to import the class LinkedList from here:
import java.util.*;
public class SetExample {
public static void main (String[] argv)
{
// Create an instance of the data structure.
LinkedList<String> favoriteShows1 = new LinkedList<String>();
// Put some elements in so that it becomes a set of strings.
favoriteShows1.add ("Yes minister");
favoriteShows1.add ("Seinfeld");
favoriteShows1.add ("Cheers");
favoriteShows1.add ("Frasier");
favoriteShows1.add ("Simpsons");
// Create a second instance and add some elements.
LinkedList<String> favoriteShows2 = new LinkedList<String>();
favoriteShows2.add ("Mad about you");
favoriteShows2.add ("Seinfeld");
favoriteShows2.add ("Frasier");
favoriteShows2.add ("Cosby show");
// Compute set intersection and the difference favoriteShows1-favoriteShows2 in separate methods:
computeIntersection (favoriteShows1, favoriteShows2);
computeDifference (favoriteShows1, favoriteShows2);
}
static void computeIntersection (LinkedList<String> listA, LinkedList<String> listB)
{
System.out.println ("Intersection:");
for (int i=0; i < listA.size(); i++) {
String s = listA.get(i);
// To be in the intersection, s needs to be in both sets.
if ( listB.contains(s) ) {
System.out.println (" " + s);
}
}
}
static void computeDifference (LinkedList<String> listA, LinkedList<String> listB)
{
System.out.println ("Difference: ");
for (int i=0; i < listA.size(); i++) {
String s = listA.get(i);
// If s is not in B, it's in the difference.
if ( ! listB.contains(s) ) {
System.out.println (" " + s);
}
}
}
}
Note:
- We need to import the class LinkedList from java.util.
- We have specialized the use of the class to store String instances:
LinkedList<String> favoriteShows1 = new LinkedList<String>();
- Notice the methods used in the LinkedList class:
- The add() method to insert new elements.
- The size() method to find out how many elements a list has.
- The get() method to get a particular element.
- The contains() method to see if a particular element is in the list.
In-Class Exercise 1:
Download this program and
implement union.
A similar example with integers:
import java.util.*;
public class SetExample3 {
public static void main (String[] argv)
{
// Create an instance of a linked list and add some data.
LinkedList<Integer> oddGuys = new LinkedList<Integer>();
oddGuys.add (1);
oddGuys.add (3);
oddGuys.add (5);
oddGuys.add (7);
oddGuys.add (9);
// Another set.
LinkedList<Integer> primes = new LinkedList<Integer>();
primes.add (1);
primes.add (2);
primes.add (3);
primes.add (5);
primes.add (7);
// Set intersection and difference.
computeIntersection (oddGuys, primes);
computeDifference (oddGuys, primes);
}
static void computeIntersection (LinkedList<Integer> listA, LinkedList<Integer> listB)
{
System.out.println ("Intersection:");
for (int i=0; i<listA.size(); i++) {
Integer K = listA.get(i);
// To be in the intersection, K needs to be in both sets.
if ( listB.contains(K) ) {
System.out.println (" " + K);
}
}
}
static void computeDifference (LinkedList<Integer> listA, LinkedList<Integer> listB)
{
System.out.println ("Difference: ");
for (int i=0; i<listA.size(); i++) {
Integer K = listA.get(i);
// If K is not in B, it's in the difference.
if ( ! listB.contains(K) ) {
System.out.println (" " + K);
}
}
}
}
We'll modify the Integer example to actually compute the
intersection and difference sets instead of printing them:
import java.util.*;
public class SetExample4 {
public static void main (String[] argv)
{
// Create an instance of a linked list and add some data.
LinkedList<Integer> oddGuys = new LinkedList<Integer>();
oddGuys.add (1);
oddGuys.add (3);
oddGuys.add (5);
oddGuys.add (7);
oddGuys.add (9);
// Another set.
LinkedList<Integer> primes = new LinkedList<Integer>();
primes.add (1);
primes.add (2);
primes.add (3);
primes.add (5);
primes.add (7);
// Set intersection and difference.
LinkedList<Integer> intersection = computeIntersection (oddGuys, primes);
// Note use of toString() in LinkedList.
System.out.println ("Intersection: " + intersection);
LinkedList<Integer> difference = computeDifference (oddGuys, primes);
System.out.println ("Difference: " + difference);
}
static LinkedList<Integer> computeIntersection (LinkedList<Integer> listA, LinkedList<Integer> listB)
{
LinkedList<Integer> listC = new LinkedList<Integer>();
for (int i=0; i<listA.size(); i++) {
Integer K = listA.get(i);
// To be in the intersection, K needs to be in both sets.
if ( listB.contains(K) ) {
listC.add (K);
}
}
return listC;
}
static LinkedList<Integer> computeDifference (LinkedList<Integer> listA, LinkedList<Integer> listB)
{
LinkedList<Integer> listC = new LinkedList<Integer>();
for (int i=0; i<listA.size(); i++) {
Integer K = listA.get(i);
// If K is not in B, it's in the difference.
if ( ! listB.contains(K) ) {
listC.add (K);
}
}
return listC;
}
}
Note:
- The return-type of the methods is now a linked list:
static LinkedList<Integer> computeIntersection (LinkedList<Integer> listA, LinkedList<Integer> listB)
{
// ...
}
- The class LinkedList has a toString() method:
LinkedList<Integer> intersection = computeIntersection (oddGuys, primes);
System.out.println ("Intersection: " + intersection);
In-Class Exercise 2:
Download this program and
implement union so that it returns a list containing the union.
In-Class Exercise 3:
Download SetExample6.java,
DataTool.java,
DataSet.java,
and the text file datafortwo.
Then, do the following:
- Compile and execute to see how the data is retrieved and
how intersection is computed.
- Draw the memory picture just before the println() in
main().
- Use this largedataset which
has a list of preferences for more than two people, and compute
all the pairwise intersections.
Our own very list data structure
Recall the methods that we used in the LinkedList class:
- An add() method to put stuff in.
- A size() method to get the size.
- A get() method to get the i-th element.
- A contains() method to see if a particular element is already in the list.
Thus, if we were to create our own data structure to do this,
it might look something like:
public class OurList {
public void add (String s)
{
// ...
}
public int size ()
{
// ...
}
public String get (int i)
{
// ...
}
// ... contains() method ...
}
In-Class Exercise 4:
What is the signature of the contains method that should be
in the template above?
We will implement such a data structure using arrays:
- We'll call the class OurListUsingArrays.
- The array itself will be internal to the class.
- Since we don't know the size ahead of time, we'll pick a large enough number for now.
Here's the program:
public class OurListUsingArrays {
// This is the array in which we'll store strings.
String[] strings = new String [100];;
// Initially, there are none.
int numStrings = 0;
public void add (String s)
{
if (numStrings < 100) {
strings[numStrings] = s;
numStrings ++;
}
}
public int size ()
{
return numStrings;
}
public String get (int i)
{
return strings[i];
}
public boolean contains (String s)
{
// Note: we need to use numStrings instead of strings.length
for (int i=0; i < numStrings; i++) {
if ( strings[i].equalsIgnoreCase(s) ) {
return true;
}
}
return false;
}
}
Note:
- The methods are quite straightforward.
- The limitation of "100" is quite artificial.
- The above class does not include the usage of such a list,
so let's write that part:
import java.util.*;
public class SetExample7 {
public static void main (String[] argv)
{
// Create an instance of the data structure.
OurListUsingArrays favoriteShows1 = new OurListUsingArrays();
favoriteShows1.add ("Yes minister");
favoriteShows1.add ("Seinfeld");
favoriteShows1.add ("Cheers");
favoriteShows1.add ("Frasier");
favoriteShows1.add ("Simpsons");
// Create a second instance and add some elements.
OurListUsingArrays favoriteShows2 = new OurListUsingArrays();
favoriteShows2.add ("Mad about you");
favoriteShows2.add ("Seinfeld");
favoriteShows2.add ("Frasier");
favoriteShows2.add ("Cosby show");
// Compute set intersection and the difference favoriteShows1-favoriteShows2
computeIntersection (favoriteShows1, favoriteShows2);
}
static void computeIntersection (OurListUsingArrays listA, OurListUsingArrays listB)
{
System.out.println ("Intersection:");
for (int i=0; i < listA.size(); i++) {
String s = listA.get(i);
// To be in the intersection, s needs to be in both sets.
if ( listB.contains(s) ) {
System.out.println (" " + s);
}
}
}
}
In-Class Exercise 5:
Download OurListUsingArrays.java
and modify SetExample8.java
to compute unions.
About our implementation:
- One disadvantage of using arrays is that we don't know the size in advance but must make enough space in our array.
- If the array is too small, we run out of space.
- If the array is too big, we may end up wasting space
⇒
Imagine creating an array of size 100,000 for small sets of size 10.
- Our name OurListUsingArrays is quite a mouthful, so
perhaps we should name it ListWithArray.
Our own linked list
A linked list solves the "unknown size" problem:
- A linked list is initially empty (no space).
- A linked list grows to occupy only as much
space as needed to store its elements.
To see how a linked list works, we'll first examine this piece
of code:
// We'll use instances of this object in main() below.
class ListItem {
String data;
ListItem next;
}
public class StrangeExample {
public static void main (String[] argv)
{
// Make one instance and put a string in the data field.
ListItem first = new ListItem();
first.data = "Yes minister";
// Make a second one.
ListItem second = new ListItem();
second.data = "Seinfeld";
// Now link them: make the first one point to the second.
first.next = second;
// Make a third and make the second point to the third.
ListItem third = new ListItem();
third.data = "Cheers";
second.next = third;
// Make a fourth etc.
ListItem fourth = new ListItem();
fourth.data = "Frasier";
third.next = fourth;
ListItem last = new ListItem();
last.data = "Simpsons";
fourth.next = last;
// Now print. Note the extensive use of the dot-operator.
System.out.println ("First: " + first.data);
System.out.println ("Second: " + first.next.data);
System.out.println ("Third: " + first.next.next.data);
System.out.println ("Fourth: " + first.next.next.next.data);
System.out.println ("Last: " + first.next.next.next.next.data);
System.out.println ("Last (alt): " + last.data);
}
}
In-Class Exercise 6:
Draw the memory picture after each new ListItem has been created.
Instead of using the dot-operator in sequence, we'll use a different
approach:
- We will track the last item in the list using a pointer.
- When a new item is to be added, we add that to the end
⇒
We'll use the "last" pointer.
Here's the program:
class ListItem {
String data;
ListItem next;
}
public class StrangeExample2 {
public static void main (String[] argv)
{
// Make one instance and put a string in the data field.
ListItem first = new ListItem();
first.data = "Yes minister";
// This is also the last one, right now.
ListItem last = first;
// Make a second one.
ListItem nextOne = new ListItem();
nextOne.data = "Seinfeld";
// Now link them: make the first one point to the second.
last.next = nextOne;
// Advance the "last" pointer.
last = nextOne;
// Make a third and make the second point to the third.
nextOne = new ListItem();
nextOne.data = "Cheers";
last.next = nextOne;
last = nextOne;
// Make a fourth etc.
nextOne = new ListItem();
nextOne.data = "Frasier";
last.next = nextOne;
last = nextOne;
// Last one.
nextOne = new ListItem();
nextOne.data = "Simpsons";
last.next = nextOne;
last = nextOne;
// Now print by repeatedly advancing the pointer.
ListItem listPointer = first;
System.out.println ("First: " + listPointer.data);
listPointer = listPointer.next;
System.out.println ("Second: " + listPointer.data);
listPointer = listPointer.next;
System.out.println ("Third: " + listPointer.data);
listPointer = listPointer.next;
System.out.println ("Fourth: " + listPointer.data);
listPointer = listPointer.next;
System.out.println ("Last: " + listPointer.data);
}
}
Note:
- It's easier to first understand the printing:
- Notice how the pointer variable listPointer starts
by pointing to the same thing that first is pointing to?
- Then observe that listPointer advances along to the
second item, then the third etc.
- Similarly, earlier in the program, the nextOne
variable (a pointer, since it's an object variable) is made
to point to a new object instance each time.
- Each time a new item is added to the end, the last
pointer is advanced along to point to the last one.
The repetition in printing suggests a loop:
class ListItem {
String data;
ListItem next;
}
public class StrangeExample3 {
public static void main (String[] argv)
{
// Make one instance and put a string in the data field.
ListItem first = new ListItem();
first.data = "Yes minister";
ListItem last = first;
// Make a second one.
ListItem nextOne = new ListItem();
nextOne.data = "Seinfeld";
last.next = nextOne;
last = nextOne;
// Make a third and make the second point to the third.
nextOne = new ListItem();
nextOne.data = "Cheers";
last.next = nextOne;
last = nextOne;
// Make a fourth etc.
nextOne = new ListItem();
nextOne.data = "Frasier";
last.next = nextOne;
last = nextOne;
// Last one.
nextOne = new ListItem();
nextOne.data = "Simpsons";
last.next = nextOne;
last = nextOne;
// Now print by repeatedly advancing the pointer - in a simple loop.
ListItem listPointer = first;
while (listPointer != null) {
System.out.println (listPointer.data);
listPointer = listPointer.next;
}
}
}
Note:
- Once again, the variable listPointer now moves along
the list, at each step pointing at the next item in the list.
- Notice the loop termination condition:
while (listPointer != null) {
// ...
}
- When the last item is added, its .next field
contains null (because it points to nothing).
- Thus, we know we've reached the end when we're pointing to null.
In-Class Exercise 7:
Download StrangeExample3.java
and add the line
System.out.println (listPointer);
inside the while-loop. Now draw the list with actual
memory addresses and show how the variable listPointer advances
along the list.
Can the code for adding new items also be compacted?
⇒
Yes, indeed:
class ListItem {
String data;
ListItem next;
}
public class StrangeExample4 {
static ListItem first = null;
static ListItem last = null;
public static void main (String[] argv)
{
// Make one instance and put a string in the data field.
first = new ListItem();
first.data = "Yes minister";
last = first;
// Add the rest.
add ("Seinfeld");
add ("Cheers");
add ("Frasier");
add ("Simpsons");
// Now print by repeatedly advancing the pointer - in a simple loop.
ListItem listPointer = first;
while (listPointer != null) {
System.out.println (listPointer.data);
listPointer = listPointer.next;
}
}
static void add (String s)
{
// Make a new instance (new list node) and add the data.
ListItem nextOne = new ListItem();
nextOne.data = s;
// Make the current last one point to the new one.
last.next = nextOne;
// Adjust the last pointer.
last = nextOne;
}
}
We're now in position to create our own linked-list:
- We will put all the code in a class called
ListWithLinks (to resemble Java's LinkedList class).
- We will name the methods add(), size(), get() and contains().
Here's the program:
class ListItem {
String data;
ListItem next;
}
public class ListWithLinks {
// Instance variables.
ListItem front = null;
ListItem rear = null;
// To keep track of the size.
int numItems = 0;
public void add (String s)
{
if (front == null) {
// The special case of an empty list needs to be handled differently.
front = new ListItem ();
front.data = s;
rear = front;
rear.next = null;
}
else {
// Just like before:
ListItem nextOne = new ListItem ();
nextOne.data = s;
rear.next = nextOne;
rear = nextOne;
}
numItems ++;
}
public int size ()
{
return numItems;
}
public String get (int i)
{
// Sanity check:
if (i >= numItems) {
return null;
}
// Otherwise, count up to the i-th item.
int count = 0;
ListItem listPtr = front;
while (count < i) {
listPtr = listPtr.next;
count ++;
}
return listPtr.data;
}
public boolean contains (String s)
{
// Sanity check.
if (front == null) {
return false;
}
// Start from the front and walk down the list. If it's there,
// we'll be able to return true from inside the loop.
ListItem listPtr = front;
while (listPtr != null) {
if ( listPtr.data.equals(s) ) {
return true;
}
listPtr = listPtr.next;
}
return false;
}
}
This class itself will be used in "main" (or elsewhere) as a
data structure:
public class ListWithLinksExample {
public static void main (String[] argv)
{
ListWithLinks favoriteShows1 = new ListWithLinks();
favoriteShows1.add ("Yes minister");
favoriteShows1.add ("Seinfeld");
favoriteShows1.add ("Cheers");
favoriteShows1.add ("Frasier");
favoriteShows1.add ("Simpsons");
ListWithLinks favoriteShows2 = new ListWithLinks();
favoriteShows2.add ("Mad about you");
favoriteShows2.add ("Seinfeld");
favoriteShows2.add ("Frasier");
favoriteShows2.add ("Cosby");
computeIntersection (favoriteShows1, favoriteShows2);
}
static void computeIntersection (ListWithLinks listA, ListWithLinks listB)
{
System.out.println ("Intersection:");
for (int i=0; i < listA.size(); i++) { // Calls the size() method in ListWithLinks
String s = listA.get(i); // Calls the get() method
if ( listB.contains(s) ) { // The contains() method
System.out.println (" " + s);
}
}
}
}
Note:
- Some nomenclature: each individual ListItem instance
in the list is called a node of the list.
- We've changed the names first and last
to the more traditional names of front and rear.
In-Class Exercise 8:
Download ListWithLinks2.java
and ListWithLinksExample2.java
and implement the printList() method in
ListWithLinks2 to print out the list.
The code in ListWithLinksExample2 calls this method.
Conceptual view of a linked-list:
- A simple conceptual view:

- With a little more detail (actual addresses):
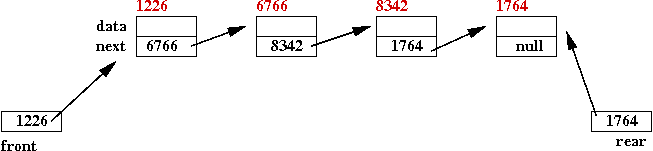
- Suppose this were a list of integers, containing the first
four odd numbers:
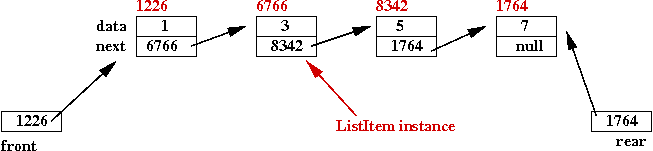
- Notice that the view is conceptual: the actual addresses do
not necessarily correspond to visual order.
- "front" and "rear" are variables that may be in other objects.
- If we were to add the data "9" to this list:

Some enhancements
We will add a couple more methods ("features") to our list:
- A toString() method.
- A way to print the list with memory addresses of the nodes.
- We'll change the name of the class to the more traditional
OurLinkedList, but different from Java's
LinkedList class.
Here's the program:
class ListItem {
// ...
}
public class OurLinkedList {
// ... same as before ...
public void add (String s)
{
// ...
}
public int size ()
{
// ...
}
public String get (int i)
{
// ...
}
public boolean contains (String s)
{
// ...
}
public String toString ()
{
if (front == null) {
return "empty";
}
// Put all the elements (data only) into the string.
String s = "[";
ListItem listPtr = front;
while (listPtr != null) {
s += " \"" + listPtr.data + "\"";
listPtr = listPtr.next;
}
return s + "]";
}
public void printWithAddresses ()
{
if (front == null) {
return;
}
ListItem listPtr = front;
while (listPtr != null) {
// listPtr's default toString() prints out the memory address.
System.out.println (" \"" + listPtr.data + "\" at address " + listPtr);
listPtr = listPtr.next;
}
}
}
Note:
- The toString() method must return a String.
⇒
We build the desired output into the String and return it.
- For printing addressees, we have exploited the fact that
when an object without a toString() method is printed,
the address is printed.
- ListItem doesn't have toString().
- Thus, printing any instance of ListItem displays
the address of that instance.
In-Class Exercise 9:
Add a toString() method to ListItem above, and
see what happens.
Doubly-linked lists
About the linked-list we've seen so far:
- We call it a singly-linked list (to contrast it with
the doubly-linked list we will see next).
- Deletion is a little difficult in a singly-linked list,
easier in a doubly-linked list.
- A doubly-linked list allows traversal in any direction.
- A singly-linked list allows traversal in only the "forward"
(front to rear) direction.
- One implication for the singly-linked list is this:
- Consider this picture:

- And this code:
public class SinglyLinkedListProblem {
public static void main (String[] argv)
{
// Some list code:
ListItem front = new ListItem ();
front.next = new ListItem ();
rear = front.next;
// Given rear, can one print the element before it?
printPrevNode (rear);
}
static void printPrevNode (ListItem listPtr)
{
// How do we go to whichever node comes before listPtr?
}
}
In a doubly-linked list:
- The conceptual view is:

- Each node points both to the next one in the list and the
previous one.
- Except for the first node, whose "backpointer" points to
null, and the last node, whose next pointer
points to null.
- Let us now add the additional pointer to the class that
used for each node:
class ListItem {
String data;
ListItem next; // To point to next node in list.
ListItem prev; // To point to the previous node in the list.
}
- We'll have to set the prev pointer carefully when
we add a new element.
Here's the program:
class ListItem {
String data;
ListItem next; // To point to next node in list.
ListItem prev; // To point to the previous node in the list.
}
public class DoublyLinkedList {
// Instance variables.
ListItem front = null;
ListItem rear = null;
int numItems = 0;
public void add (String s)
{
if (front == null) {
// Similar to singly-linked list, except for setting rear.prev
front = new ListItem ();
front.data = s;
rear = front;
rear.next = null;
rear.prev = null; // Must set this correctly.
}
else {
// Make new ListItem and set its fields correctly.
ListItem nextOne = new ListItem ();
nextOne.data = s;
nextOne.next = null;
nextOne.prev = rear;
// Adjust the next pointer of the current last one, and adjust rear itself.
rear.next = nextOne;
rear = nextOne;
}
numItems ++;
}
public int size ()
{
// ...
}
public String get (int i)
{
// ... same as in singly-linked list ...
}
public boolean contains (String s)
{
// ... same as in singly-linked list ...
}
public String toString ()
{
// ...
}
}
Note:
- The size(), get() and contains() methods are
the same as in a singly-linked list because those don't need the
prev pointer.
In-Class Exercise 10:
Download DoublyLinkedList2.java
and DoublyLinkedListExample2.java
and implement a method to print the list in reverse (starting from
the rear).
Next, let's examine what needs to change to build a doubly-linked list
that can store int's.
In-Class Exercise 11:
Download DoublyLinkedIntList.java
and DoublyLinkedListExample3.java
and implement a doubly-linked list to hold integers.
You can copy over the code in DoublyLinkedList above into
your DoublyLinkedIntList to begin with, and then change
methods/data etc so that the list stores int's.
Deletion
There are many ways by which we might want to delete a particular
element:
- For example, we might want do it by identifying the element directly:
DoublyLinkedList favoriteShows = new DoublyLinkedList();
favoriteShows.add ("Crocodile Hunter");
// ... add more stuff ...
favoriteShows.delete ("Crocodile Hunter");
- Alternatively, we might want to delete by order of occurence in list:
DoublyLinkedList favoriteShows = new DoublyLinkedList();
favoriteShows.add ("Crocodile Hunter");
// ... add more stuff ...
favoriteShows.delete (0); // Delete 0-th element.
- What needs to happen in a deletion?
- We need to find the node in question.
- For example, suppose we want to delete the third node.
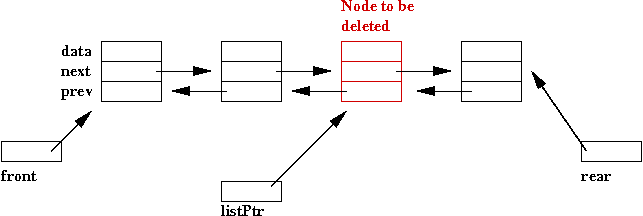
- The "gap" after removal needs to be "stitched together" by
adjusting links.
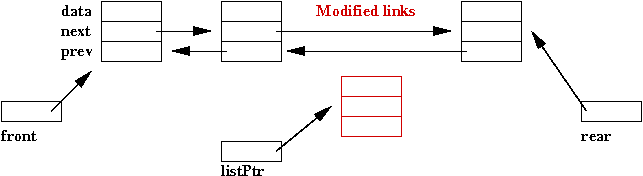
Here's the program:
class ListItem {
// ...
}
public class DoublyLinkedList4 {
// ...
public void add (String s)
{
// ...
}
public int size ()
{
// ...
}
public String get (int i)
{
// ...
}
public boolean contains (String s)
{
// ...
}
public String toString ()
{
// ...
}
// Find String s and delete it if it occurs in the list.
public void delete (String s)
{
ListItem listPtr = front;
while ( (listPtr != null) && (! listPtr.data.equals(s)) ) {
listPtr = listPtr.next;
}
// If it's not there, return.
if (listPtr == null) {
return;
}
// Otherwise delete: four cases.
if (front == rear) {
// Case 1: only one element.
front = rear = null;
}
else if (listPtr == front) {
// Case 2: we're deleting from the front.
front = listPtr.next;
front.prev = null;
}
else if (listPtr == rear) {
// Case 3: delete the last element.
rear = listPtr.prev;
rear.next = null;
}
else {
// Case 4: In the middle: stitch the prev and next nodes together.
listPtr.prev.next = listPtr.next;
listPtr.next.prev = listPtr.prev;
}
numItems --;
}
// Delete the element at a particular position in the list
public void delete (int i)
{
// Check for bad input.
if ( (i < 0) || (i >= numItems) ) {
return;
}
// Find the i-th element.
int count = 0;
ListItem listPtr = front;
while ( (listPtr != null) && (count != i) ) {
listPtr = listPtr.next;
count ++;
}
// Otherwise delete: four cases.
if (front == rear) {
// Case 1: only one element.
front = rear = null;
}
else if (listPtr == front) {
// Case 2: we're deleting from the front.
front = listPtr.next;
front.prev = null;
}
else if (listPtr == rear) {
// Case 3: delete the last element.
rear = listPtr.prev;
rear.next = null;
}
else {
// Case 4: In the middle: stitch the prev and next nodes together.
listPtr.prev.next = listPtr.next;
listPtr.next.prev = listPtr.prev;
}
numItems --;
}
}
In-Class Exercise 12:
Modify DoublyLinkedList4.java
above to print out the addresses of the node-to-be-deleted, along with
the nodes on either side. Then, draw "before" and "after" lists
complete with addresses.
Use DoublyLinkedListExample4.java
as the class with main().
Deletion in a singly-linked list:
- Deletion is a little more complicated in a singly linked list.
- Example: suppose we want to delete the data "7" (4-th node)
in this list of integers:

- First, we walk down the list to find the node:
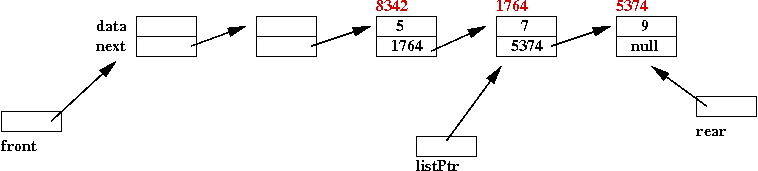
- To remove the node, we have to make the previous node point
to the next one:
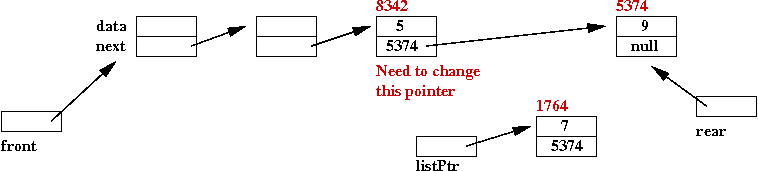
- How do we "reach" the previous node in order to change the pointer?
⇒
We need another pointer variable:
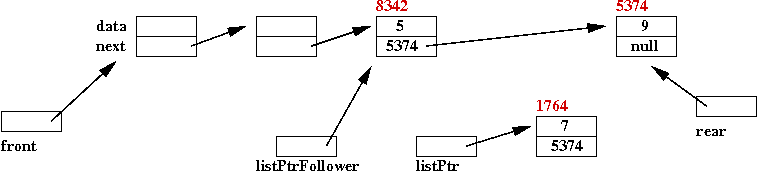
- This pointer variable needs to "move" along with the listPtr
variable when we search for the node to be deleted:
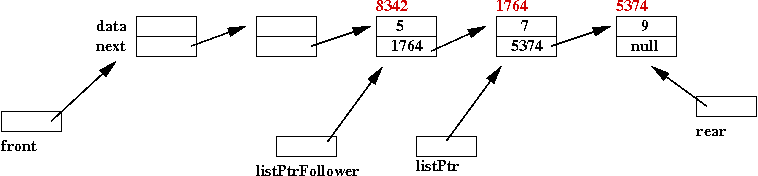
In-Class Exercise 13:
Write on paper the code needed to search the list for both
the item-to-be-deleted and the node prior to it.
Then write on paper the code needed for deletion.
In-Class Exercise 14:
Implement your code in OurLinkedList2.java
and test it with OurLinkedListExample2.java.
© 2006-2020, Rahul Simha & James Taylor (revised 2020)












