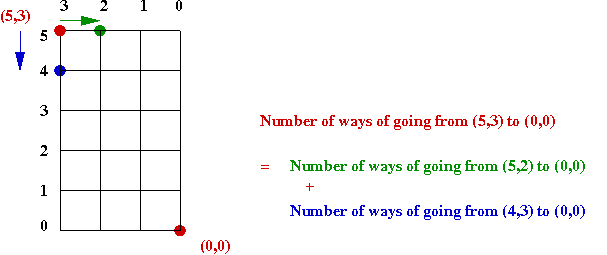Module 4: Recursion, Part I
Supplemental material
A simple example
We'll start by looking at a simple example:
- We'll use repeated multiplication to compute the "powers" of an integer.
- Thus, 24 = 2 x 2 x 2 x 2 = 16.
First, let's consider the straightforward way, using a loop:
public class PowerWithIteration {
public static void main (String[] argv)
{
int p = power (3, 2);
System.out.println ( "3^2 = " + p);
p = power (3, 4);
System.out.println ( "3^4 = " + p);
p = power (2, 8);
System.out.println ( "2^8 = " + p);
}
static int power (int a, int b)
{
int p = 1; // a^0
while (b > 0) {
p = p * a; // b times through loop.
b --;
}
return p;
}
}
Next, let's look at the recursive version of the same:
public class PowerExample {
public static void main (String[] argv)
{
int p = power (3, 2);
System.out.println ( "3^2 = " + p);
p = power (3, 4);
System.out.println ( "3^4 = " + p);
p = power (2, 8);
System.out.println ( "2^8 = " + p);
}
static int power (int a, int b)
{
int p;
if (b == 0) {
p = 1;
}
else {
// Note use of recursion:
p = a * power (a, b-1);
}
return p;
}
}
How does this work?
- Each successive call reduces b by 1, and so
eventually, b==0.
- When b==0, the if-clause executes, which causes
a cascade of return's to previous invocations of the method.
- The key is: successive (recursive) calls to power()
must change something (in this case, b) each time
so that there's an end to it.
- Note that a did not change at all - it's like
a regular parameter that's intended to pass on a value for use
in a computation.
⇒
It's not used in determining how the computation proceeds.
To see what's happening more clearly, we'll print something in
each call:
public class PowerExample2 {
public static void main (String[] argv)
{
// We added a third parameter to track which call we're in.
int p = power (3, 2, 0);
System.out.println ( "3^2 = " + p);
p = power (3, 4, 0);
System.out.println ( "3^4 = " + p);
p = power (2, 8, 0);
System.out.println ( "2^8 = " + p);
}
static int power (int a, int b, int level)
{
// Print the "level", along with extra blanks.
System.out.println ( makeBlanks(level) + "Level " + level + ": b=" + b );
int p;
if (b == 0) {
p = 1;
}
else {
p = a * power (a, b-1, level+1);
}
// Now the result.
System.out.println ( makeBlanks(level) + "Level " + level + ": p=" + p );
return p;
}
static String makeBlanks (int n)
{
String str = "";
for (int i=0; i < n; i++) {
str += " ";
}
return str;
}
}
Here's some of the output, annotated:
Level 0: b=2 // The first time power() is called a=3, b=2
Level 1: b=1 // First recursion: b=1
Level 2: b=0 // Second recursion: b=0
Level 2: p=1 // No further recursion: "bottom out" case when b=0
Level 1: p=3 // Back to first recursion, when b=1
Level 0: p=9 // Back to first call, when b=2
3^2 = 9
Level 0: b=4 // First time power() is called with a=3, b=4
Level 1: b=3 // First recursion: b=3
Level 2: b=2 // Second recursion: b=2
Level 3: b=1 // Third recursion: b=1
Level 4: b=0 // Fourth recursion: b=0
Level 4: p=1 // Bottom out and return p=1
Level 3: p=3 // Back to 3rd recursion, compute p=3
Level 2: p=9 // Back to 2nd recursion, compute p=9
Level 1: p=27 // Back to 1st recursion, p=27 now
Level 0: p=81 // Back to original call, p=81 (final result to return to main)
3^4 = 81
To see this a little differently, let's examine the state of
memory during these calls for the 32 case.
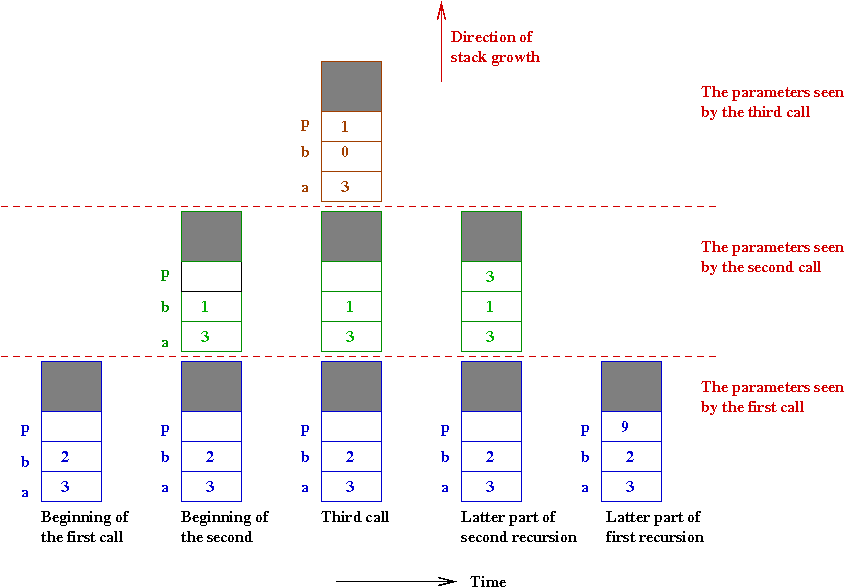
- The part of memory we are looking at is the stack.
- Whenever a method call occurs, a part of the stack is used
for the local variables (p above) and parameters (a,
b).
- When a method completes execution, its space on the stack
"disappears".
- When one method calls another, the second method is now given
space on the stack.
- The first method's stuff is still on the stack, available when
it starts executing again.
- Thus, in the example above:
- When the first call to power() is made from main,
the stack looks like the leftmost picture: a=3, b=2
(and p is undetermined).
- When the second call occurs, the stack grows to allocate
exactly the same "template" of space for the second call.
- Now the parameter b==1. The parameter a==3.
- Half-way through the second call, there's another recursive call
⇒ the third time we enter power().
- In the third call, b==0.
- The third call does not recurse and instead returns 1.
- This return value goes is captured in the second call, and
multiplies into a==3. This makes p==3 in the
latter part of the second call.
- Then the second call returns 3, which goes into the
first call. There, it gets multiplied by a==3 to make
p==9.
- Finally, p==9 is returned to main().
- Phew!
- Note that the pictures show a grey box within each part of a
method's allocated space on the stack: this is other bookkeeping stuff
needed by Java to handle method calls.
In-Class Exercise 1:
Show (on paper) what happens when 43 is computed using
the above program. Draw the stack at each step.
Next, we will point out that the original example with
recursion could have been written more "tightly" (compactly) as
follows:
public class PowerExample3 {
public static void main (String[] argv)
{
// ...
}
static int power (int a, int b)
{
if (b == 0) {
return 1;
}
return (a * power (a, b-1));
}
}
Note:
- This does not change the execution.
- The code is merely more compact.
In-Class Exercise 2:
Download Sum.java and implement
a recursive method to compute the sum of the first n integers.
Now for another example:
- The factorial of an integer n is defined as:
n! = n x (n-1) x (n-2) ... 2 x 1
- For example, 5! = 5 x 4 x 3 x 2 x 1 = 120.
- Thus, you multiply n by n-1, then multiply the
result by n-2 ... and so on, until you multiply by 1.
Here's a recursive implementation of factorial:
public class FactorialExample {
public static void main (String[] argv)
{
System.out.println ( "3! = " + factorial(3) );
System.out.println ( "5! = " + factorial(5) );
System.out.println ( "5! x 3! = " + (factorial(3) * factorial(5)) );
}
static int factorial (int n)
{
if (n == 1) {
return 1;
}
return ( n * factorial(n-1) );
}
}
In-Class Exercise 3:
Modify the above program
to provide the kind of indented
printing we did for the power example:
- Copy over the makeBlanks() method.
- Add another "level" parameter and the appropriate println's.
We need to point out one more important idea:
- In the factorial example, there was only one parameter.
- In the power example, there were two parameters
static int power (int a, int b)
{
// ...
}
In this case, b is the parameter that changes and
controls the recursion.
- The parameters a is not essential to the recursion
itself. To see this, let's make a into a global:
public class PowerExample4 {
// Declare "a" as global to be set in main() and accessed elsewhere.
static int a;
public static void main (String[] argv)
{
a = 3;
int p = power (2); // Only "b" is passed as parameter.
System.out.println ( "3^4 = " + p);
p = power (4);
System.out.println ( "3^4 = " + p);
a = 2;
p = power (8);
System.out.println ( "2^8 = " + p);
}
// Only one parameter.
static int power (int b)
{
int p;
if (b == 0) {
p = 1;
}
else {
p = (a * power (b-1));
}
System.out.println ("Intermediate result: " + a + "^" + b + "=" + p);
return p;
}
}
In-Class Exercise 4:
Implement and execute the above program. Explain what you see and
why making a a global variable does not affect the output.
Next, let's see what happens when b is a global variable:
public class PowerExample5 {
// Declare "a" as global to be set in main() and accessed elsewhere.
static int a;
// Now try "b"
static int b;
public static void main (String[] argv)
{
a = 3;
b = 2;
int p = power (); // No parameters.
System.out.println ( "3^2 = " + p);
b = 4;
p = power ();
System.out.println ( "3^4 = " + p);
a = 2;
b = 8;
p = power ();
System.out.println ( "2^8 = " + p);
}
// No parameter.
static int power ()
{
int p;
if (b == 0) {
p = 1;
}
else {
b = b - 1;
p = a * power();
}
System.out.println ("Intermediate result: " + a + "^" + b + "=" + p);
return p;
}
}
In-Class Exercise 5:
Download and execute the above parameter-less version. Explain the output.
Searching an array via recursion
We know how to loop through an array to search for a particular value.
Let's see how this can be done using recursion:
public class ArraySearch {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = makeRandomArray (10);
// A random search term.
int searchTerm = UniformRandom.uniform (1, 100);
// Call the recursive search method.
boolean found = search (A, searchTerm, 0);
System.out.println ("found=" + found);
}
static boolean search (int[] A, int value, int index)
{
// Two "bottom out" cases:
if (index >= A.length) {
return false;
}
if (A[index] == value) {
return true;
}
// Else try further into the array:
return search (A, value, index+1);
}
static int[] makeRandomArray (int length)
{
// ... we've seen this before ...
}
}
Note:
- There are three parameters to search(), only one of
which (index) controls the recursion.
- In this example, there are two ways in which the recursion
can bottom out:
- We exceed the length of the array
⇒ we couldn't find the element and so we return
false
- We found the element, and return true.
- The search starts at position 0.
- The example shares the characteristic features of a
recursive method:
- There is at least one parameter that controls the recursion.
- This parameter (possibly others too) must be checked in the bottom-out cases.
- The problem size must reduce with each recursive call, by
changing at least one of the controlling parameters.
In-Class Exercise 6:
Thinking exercise: what would happen if we switched the two
if-statements in the search() method?
static boolean search (int[] A, int value, int index)
{
if (A[index] == value) {
return true;
}
if (index >= A.length) {
return false;
}
return search (A, value, index+1);
}
Palindrome checking
We'll use the following idea to check whether a string
is a palindrome:
- If the first and last letters are equal, then the string
obtained by removing them must itself be a palindrome.
Here's the program:
public class Palindrome {
public static void main (String[] argv)
{
String str = "redder";
System.out.println ( str + " " + checkPalindrome(str) );
str = "river";
System.out.println ( str + " " + checkPalindrome(str) );
str = "neveroddoreven";
System.out.println ( str + " " + checkPalindrome(str) );
}
static String checkPalindrome (String str)
{
// Two bottom out cases:
if ( (str.length() == 0) || (str.length() == 1) ) {
return "is a palindrome";
}
if ( str.charAt(0) != str.charAt(str.length()-1) ) {
return "is not a palindrome";
}
// First and last letters matched. Remove them and check remaining recursively.
String nextStr = str.substring (1, str.length()-1);
return checkPalindrome (nextStr);
}
}
Note:
- The return value is a String. We could also have
written it to return true or false.
In-Class Exercise 7:
Download Palindrome2.java
and make the recursive method checkPalindrome() work
for char arrays (instead of String's).
Solving a combinatorial problem using recursion
Consider this problem of seating people in a row of seats:
- There is a panel of important speakers, all seated in a row.
- There are K speakers, each of whom need to be
assigned a seat on the panel (a place to sit).
- There are M seats, where M >= K.
- Question: in how many ways can the seating be arranged?
- For example, with K=2 speakers and M=3 seats,
there are 6 possible seating arrangements:
1 2 _
1 _ 2
2 1 _
2 _ 1
_ 1 2
_ 2 1
First let's solve the problem of merely counting the number of
such arrangements:
public class PermutationSeating {
public static void main (String[] argv)
{
int numSeats = 3; // M
int numPeople = 2; // K
int n = countPermutations (numSeats, numPeople);
System.out.println (numPeople + " can sit on " + numSeats + " seats in " + n + " different arrangements");
}
static int countPermutations (int numSpaces, int numRemaining)
{
// Given numRemaining to assign among numSpaces seats,
// count all possible arrangements.
// Bottom out case: if none are remaining, there's only one way to do that.
if (numRemaining == 0) {
return 1;
}
// Otherwise, obtain the count for a smaller version of the problem.
int n = countPermutations (numSpaces-1, numRemaining-1);
// Since one person can chose from among numSpaces, there
// numSpaces ways of doing that, which we multiply with n.
return (numSpaces * n);
}
}
Note:
- The reasoning is that, if we are to assign K people
among M seats, then
- We count the number of ways one of them can be assigned to a
seat (M ways).
- We count the number of ways K-1 people (remaining
people) can be assigned to the remaining M-1 seats.
- We multiply these two numbers.
Now let's modify the program to print the actual permutations:
import java.util.*;
public class PermutationSeating2 {
// We'll use a global to count the number of permutations.
static int count;
public static void main (String[] argv)
{
// Test case 1: M=3, K=2.
int numSeats = 3;
int numPeople = 2;
int[] seats = new int [numSeats];
count = 0;
printPermutations (numSeats, numPeople, seats, 1);
System.out.println (" ⇒ " + count + " permutations");
// Test case 1: M=5, K=2.
numSeats = 5;
numPeople = 2;
seats = new int [numSeats];
count = 0;
printPermutations (numSeats, numPeople, seats, 1);
System.out.println (" ⇒ " + count + " permutations");
}
static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
{
// Bottom-out case. Note that we are printing here, since each time
// we get here we complete one permutation.
if (numRemaining == 0) {
// Print.
System.out.println ( Arrays.toString(seats) );
// Remember to increment the number of permutations found.
count ++;
return;
}
// Otherwise, non-base case: look for an empty spot for "person"
for (int i=0; i < seats.length; i++) {
if (seats[i] == 0) {
// Empty spot.
seats[i] = person;
// Recursively assign remaining, starting with person+1
printPermutations (numSpaces-1, numRemaining-1, seats, person+1);
// Important: we need to un-do the seating for other trials.
seats[i] = 0;
}
} //end-for
}
}
Note:
- The code is now a little different.
- We use an array (seats[]) to record permutations:
⇒
The array represents seats, into which we put particular people.
- There are now two more parameters to the recursive method:
static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
- We've added the actual seating arrangement (seats[])
that we'll need for printing at the very end.
- We pass on the actual person being seated in this particular call.
- The key ideas:
- First seat person 1, then person 2, etc.
- Whenever we seat person i, we find an available spot,
then recursively seat the others starting with i+1.
- Once we seat the last person, we're ready to print the
current seating.
- Most important:
- Each time we seat someone, we need to un-do that seating
when we generate the next possibility:
// Try a seat.
seats[i] = person;
// Recursively assign remaining, starting with person+1
printPermutations (numSpaces-1, numRemaining-1, seats, person+1);
// Important: now un-do the seating for the next iteration of the loop.
seats[i] = 0;
- The output of the program is:
[1, 2, 0]
[1, 0, 2]
[2, 1, 0]
[0, 1, 2]
[2, 0, 1]
[0, 2, 1]
⇒ 6 permutations
[1, 2, 0, 0, 0]
[1, 0, 2, 0, 0]
[1, 0, 0, 2, 0]
[1, 0, 0, 0, 2]
[2, 1, 0, 0, 0]
[0, 1, 2, 0, 0]
[0, 1, 0, 2, 0]
[0, 1, 0, 0, 2]
[2, 0, 1, 0, 0]
[0, 2, 1, 0, 0]
[0, 0, 1, 2, 0]
[0, 0, 1, 0, 2]
[2, 0, 0, 1, 0]
[0, 2, 0, 1, 0]
[0, 0, 2, 1, 0]
[0, 0, 0, 1, 2]
[2, 0, 0, 0, 1]
[0, 2, 0, 0, 1]
[0, 0, 2, 0, 1]
[0, 0, 0, 2, 1]
⇒ 20 permutations
Next, we'll look at another way to handle the un-do part of the
program:
public class PermutationSeating3 {
static int count;
public static void main (String[] argv)
{
// ...
}
static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
{
if (numRemaining == 0) {
System.out.println ( Arrays.toString(seats) );
count ++;
return;
}
// Look for an empty spot.
for (int i=0; i < seats.length; i++) {
if (seats[i] == 0) {
// Make a copy so that we don't need to un-do.
int[] seatsCopy = copy (seats);
// Assign and recurse.
seatsCopy[i] = person;
printPermutations (numSpaces-1, numRemaining-1, seatsCopy, person+1);
// Don't need this: seats[i] = 0;
}
}
}
static int[] copy (int[] A)
{
int[] B = new int [A.length];
for (int i=0; i < A.length; i++) {
B[i] = A[i];
}
return B;
}
}
Note:
- This time, we make changes to a fresh copy of the array.
- The copy is what is passed down into the recursion.
Next we'll solve a slight variation of the problem:
- Suppose that we want to count the number of
seating-permutations where person 1 does NOT sit at the ends.
- Thus, seats 0 and M-1 are "banned" for person 1.
- To solve the problem, we modify the code to test for this case.
Here's the program:
public class PermutationSeating4 {
static int count;
public static void main (String[] argv)
{
// ...
}
static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
{
if (numRemaining == 0) {
// Print.
System.out.println ( Arrays.toString(seats) );
count ++;
return;
}
// Look for an empty spot for this person.
for (int i=0; i < seats.length; i++) {
// Check for "banned" configuration:
if (person == 1) {
if ( (i == 0) || (i == seats.length-1) ) {
// Person 1 can't sit at the ends.
// Skip to next loop iteration.
continue;
}
}
// We reach here if it's ok to explore further.
if (seats[i] == 0) {
// Empty spot.
seats[i] = person;
printPermutations (numSpaces-1, numRemaining-1, seats, person+1);
seats[i] = 0;
}
}
}
}
Another combinatorial example
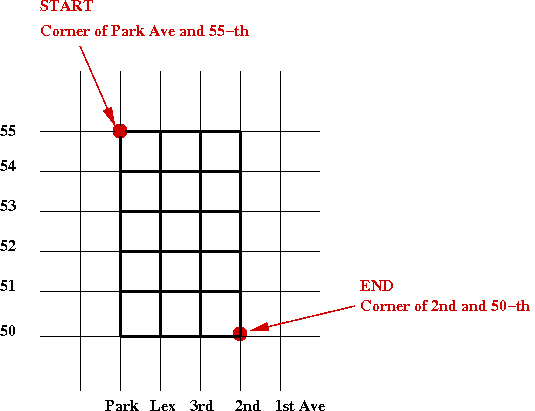
Consider this problem:
- Suppose we are at a Manhattan intersection and want to go to
another intersection:
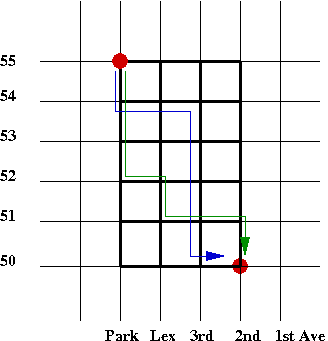
- There are many alternate paths, each of which has the same
length (as short as possible). Here are two, for example:
- Goal: We want to compute the number of such possible paths.
- First, we'll simplify this to a simple grid:
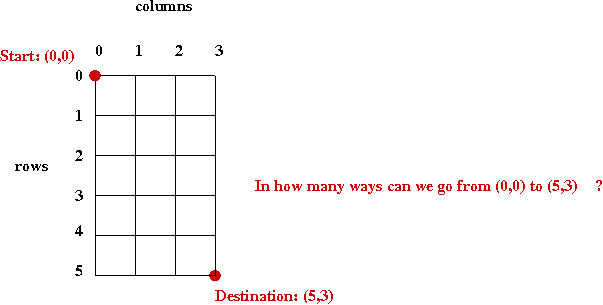
- This is the key insight:
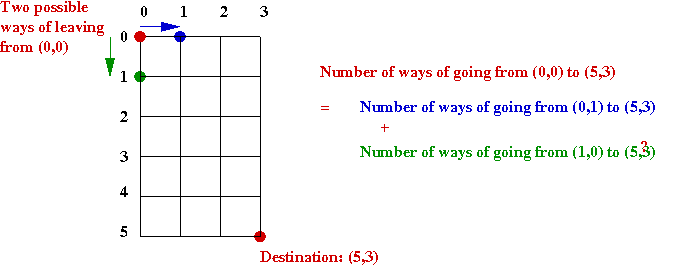
- Which we can alternatively write as getting from (5,3) to
(0,0):
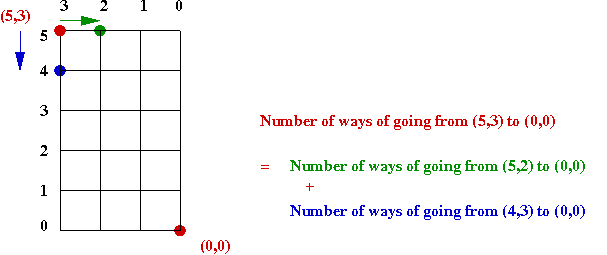
- Thus, we can recursively compute each of the smaller
sub-problems and add them to get the larger one.
Here's the program:
public class Manhattan {
public static void main (String[] argv)
{
// Test case 1: go from (1,1) to (0,0)
int r = 1, c = 1;
int n = countPaths (r, c);
System.out.println ("r=" + r + " c=" + c + " ⇒ n=" + n);
// Test case 2: go from (2,2) to (0,0)
r = 2;
c = 2;
n = countPaths (r, c);
System.out.println ("r=" + r + " c=" + c + " ⇒ n=" + n);
// Test case 2: go from (5,7) to (0,0)
r = 5;
c = 7;
n = countPaths (r, c);
System.out.println ("r=" + r + " c=" + c + " ⇒ n=" + n);
}
static int countPaths (int numRows, int numCols)
{
// Bottom out case: there's only one way to (0,0).
// Note: it's || and not &&.
if ( (numRows == 0) || (numCols == 0) ) {
return 1;
}
// Otherwise, reduce to two sub-problems and add.
int downCount = countPaths (numRows-1, numCols);
int rightCount = countPaths (numRows, numCols-1);
return (downCount + rightCount);
}
}
Note:
- The recursive method countPaths() has two recursive
calls:
- The first one creates the sub-problem with fewer rows:
int downCount = countPaths (numRows-1, numCols);
- The second creates the sub-problem with fewer columns.
int rightCount = countPaths (numRows, numCols-1);
In-Class Exercise 8:
Consider the code above:
- Why is it that we need || (OR) in the if
condition? What would happen if we replaced that with && (AND)?
- So, in fact, how many ways are there to get from the corner
of Park and 55-th to the corner of 2nd and 50th?
Let's now modify the code to print out the different paths:
- For example, for (2,2) to (0,0), we want the output to look like:
[2,2] -> [1,2] -> [0,2] -> [0,1] -> [0,0]
[2,2] -> [1,2] -> [1,1] -> [0,1] -> [0,0]
[2,2] -> [1,2] -> [1,1] -> [1,0] -> [0,0]
[2,2] -> [2,1] -> [1,1] -> [0,1] -> [0,0]
[2,2] -> [2,1] -> [1,1] -> [1,0] -> [0,0]
[2,2] -> [2,1] -> [2,0] -> [1,0] -> [0,0]
(There are 6 different paths.)
- To solve the problem, we'll pass along a String
that we append to as we go along in the recursion.
- As soon as we bottom out, we have a full path that we can print.
Here's the program:
public class Manhattan2 {
public static void main (String[] argv)
{
// Test case 1:
int r = 1, c = 1;
int n = countPaths (r, c, "[1,1]");
System.out.println ("r=" + r + " c=" + c + " ⇒ n=" + n);
// Test case 2:
r = 2;
c = 2;
n = countPaths (r, c, "[2,2]");
System.out.println ("r=" + r + " c=" + c + " ⇒ n=" + n);
}
static int countPaths (int numRows, int numCols, String partialPath)
{
// Bottom out case: this is more complicated now.
if (numRows == 0) {
// Make the path across the columns.
String finalStr = partialPath;
for (int c=numCols-1; c>=0; c--) {
finalStr += " -> [0," + c + "]";
}
System.out.println (finalStr);
return 1;
}
else if (numCols == 0) {
// Make the path down rows.
String finalStr = partialPath;
for (int r=numRows-1; r>=0; r--) {
finalStr += " -> [" + r + ",0]";
}
System.out.println (finalStr);
return 1;
}
// Otherwise, reduce problem size.
// Downwards.
String downpathStr = partialPath + " -> " + "[" + (numRows-1) + "," + numCols + "]";
int downCount = countPaths (numRows-1, numCols, downpathStr);
// Rightwards.
String rightpathStr = partialPath + " -> " + "[" + (numRows) + "," + (numCols-1) + "]";
int rightCount = countPaths (numRows, numCols-1, rightpathStr);
// Add the two.
return (downCount + rightCount);
}
}
Note:
- Essentially, what we are doing is this:
- The path will be represented using a String.
- We build this string as we go down the recursion, ending in
the bottom-out condition.
- We print when we bottom-out, because by then we have the path
that ended there.
- The bottom-out is itself more complicated here:
- What needs to be printed is different for "ending in the last
column" versus "ending in the last row".
-
In-Class Exercise 9:
Suppose we want the output to number the paths as follows:
Path #1: [2,2] -> [1,2] -> [0,2] -> [0,1] -> [0,0]
Path #2: [2,2] -> [1,2] -> [1,1] -> [0,1] -> [0,0]
Path #3: [2,2] -> [1,2] -> [1,1] -> [1,0] -> [0,0]
Path #4: [2,2] -> [2,1] -> [1,1] -> [0,1] -> [0,0]
Path #5: [2,2] -> [2,1] -> [1,1] -> [1,0] -> [0,0]
Path #6: [2,2] -> [2,1] -> [2,0] -> [1,0] -> [0,0]
Modify Manhattan2.java above
to number paths.
Unnecessary recursion
Recursion is not always the best solution:
- In many cases, simple iteration works fine and may be easier to write.
- Example: searching in an array.
Sometimes, recursion can be downright wasteful, as we'll see
in the next example.
Let's consider a recursive program to compute Fibonacci numbers.
- The standard Fibonacci sequence is:
1st Fibonacci number: 0
2nd Fibonacci number: 1
3rd Fibonacci number: 1
4th Fibonacci number: 2
5th Fibonacci number: 3
6th Fibonacci number: 5
7th Fibonacci number: 8
...
- Thus, to get the n-th Fibonacci number fn,
you add the previous two Fibonacci numbers:
⇒
fn = fn-1 + fn-2
- This is an obvious candidate for recursion.
Here's the program:
public class Fibonacci {
public static void main (String[] argv)
{
// Test case 1:
int n = 5;
int f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f);
// Test case 2:
n = 20;
f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f);
}
static int fibonacci (int n)
{
// Base cases:
if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
// f_n = f_{n-1} + f_{n-2}
int f_n_minus_one = fibonacci (n-1);
int f_n_minus_two = fibonacci (n-2);
return f_n_minus_one + f_n_minus_two;
}
}
Thus, previous terms are computed recursively.
The program can be written more compactly:
public class Fibonacci2 {
public static void main (String[] argv)
{
// ...
}
static int fibonacci (int n)
{
// Base cases rolled into one:
if (n <= 2) {
return (n-1);
}
return ( fibonacci(n-1) + fibonacci(n-2) );
}
}
Let us now count how often the recursive method fibonacci()
is called:
public class Fibonacci3 {
// A counter, accessible everywhere.
static int numCalls;
public static void main (String[] argv)
{
// Test case 1:
int n = 5;
// Need to initialize:
numCalls = 0;
int f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f + " numCalls=" + numCalls);
// Test case 2:
n = 20;
// Need to initialize:
numCalls = 0;
f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f + " numCalls=" + numCalls);
}
static int fibonacci (int n)
{
// We are recording the number of times this method is called.
numCalls ++;
if (n <= 2) {
return (n-1);
}
return ( fibonacci(n-1) + fibonacci(n-2) );
}
}
Note:
- For n=5, it's not so bad: 9 calls.
- However, for n=20, there are 13,529 calls.
In-Class Exercise 10:
Before reading further, can you see why there are so many calls?
To fix the problem:
- We will store computed values in an array.
- If previous values are needed and already stored, then we
avoid making a recursive call.
Here's the program:
public class Fibonacci4 {
// Same counter as before.
static int numCalls;
// We'll use an array to record previously computed values:
static int[] fValues;
public static void main (String[] argv)
{
// Test case 1:
int n = 5;
// Initialize both the counter and the array:
numCalls = 0;
fValues = new int [n+1];
int f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f + " numCalls=" + numCalls);
// Test case 2:
n = 20;
// Initialize both the counter and the array:
numCalls = 0;
fValues = new int [n+1];
f = fibonacci (n);
System.out.println ("f(" + n + ") = " + f + " numCalls=" + numCalls);
}
static int fibonacci (int n)
{
// We are recording the number of times this method is called.
numCalls ++;
if (n <= 2) {
// First time we reach here, we store the values.
fValues[n] = n-1;
return (n-1);
}
// If the values haven't been computed, then compute and store.
if (fValues[n-1] == 0) {
fValues[n-1] = fibonacci(n-1);
}
if (fValues[n-2] == 0) {
fValues[n-2] = fibonacci(n-2);
}
// By the time we reach here, previous fib values have been stored.
fValues[n] = fValues[n-1] + fValues[n-2];
return fValues[n];
}
}
Now the results are reasonable:
- For n=5: there are 5 calls.
- For n=20: there are 20 calls.
- Thus, the number calls grows linearly with n.
- However, it does require more space.
Of course, Fibonacci numbers can be computed without arrays very
easily in an iterative manner:
public class Fibonacci5 {
public static void main (String[] argv)
{
// ...
}
static int fibonacci (int n)
{
// Base cases: same as in recursive version.
if (n == 1) {
return 0;
}
else if (n == 2) {
return 1;
}
// Now we know n >= 3.
// Start with first and second terms.
int fPrev = 1;
int fPrevPrev = 0;
int f = -1;
// A simple iteration takes us to the n-th term.
for (int k=3; k <= n; k++) {
f = fPrev + fPrevPrev;
fPrevPrev = fPrev;
fPrev = f;
}
return f;
}
}
In-Class Exercise 11:
Download ManhattanWithCallCount.java
and modify to count the number of recursive calls made for the
Manhattan-path problem we studied earlier.
Next, modify to include stored values and see how that reduces the
number of calls made.
© 2006-2020, Rahul Simha & James Taylor (revised 2020)