Module 3: Sorting
Supplemental material
Visualizing and interacting with sorting
Throughout this module, you might struggle with visualizing how a particular sorting strategy works and how it might differ from another sorting strategy. This is where a deck of cards will help you interact with each sort so that you can see and feel the differences. You don't need to involve the whole deck either, just sorting within one suit will help you bridge the gap.

As a warm up, try the following...
Shuffle a set of cards then lay them out from top to bottom, side-by-side on a table. Now consider these different strategies...
- Find the smallest value card, move it to the front. Find the next smallest, put it next. Repeat this process until the cards are sorted.
- Compare the value of the first card with the value of the second card. If the second card is smaller than the first card, swap the two cards. Repeat this comparison between the second and third card. Continue repeating this process until you reach the end. If the cards are not sorted, start over again at the beginning.
- Take the first card and place it at the beginning of a new row of cards. Take the second card from the original row, place it at the end of the new row, compare the last card in the new row with the card in front of it, and if the end card is smaller than the one before it then swap them. Take the third card from the original row, place it at the end of the new row, compare the last card in the new row as before and swap if necessary, and repeat this for all preceding cards in the new row. Repeat this process for all cards in the original row until the original row is empty and the new row is sorted.
- Look at the first card, if the first card is less than or equal to the middle value 7, place it in a pile to the left; otherwise place it in a pile to the right. Repeat this until you have divided all cards into the appropriat left or right pile. Take the left pile and compute the middle value, i.e. (7-1)/2 = 3, then repeat the same process as before on this subpile. You should have 3 piles, left-of-left(1-3), right-of-left(4-7), and right (8-K). Repeat this process on the left cards until you have 7 individual piles, keeping track of the order of the piles as the order of the piles should be the same order as the values. Then repeat this process for the original right pile and you should end up with 6 piles again keeping track of the order of the piles. Stack the left-most pile ontop of its neighbor and repeat this for all piles. The new stack should be sorted.
How would you do it? Do you have another solution?
Selection: a prelude to sorting
First consider the selection problem: finding the min and max
in an array:
import java.util.*;
public class FindExtremes {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = makeRandomArray (10);
// Find largest and smallest elements.
int smallest = findSmallest (testData);
int largest = findLargest (testData);
// Print.
System.out.println ("Smallest=" + smallest + ", largest=" + largest + " in array " + Arrays.toString(testData));
}
static int findSmallest (int[] A)
{
// Start by assuming first is smallest.
int smallest = A[0];
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
}
}
return smallest;
}
static int findLargest (int[] A)
{
// Similar to findSmallest except for if-condition.
int largest = A[0];
for (int i=1; i < A.length; i++) {
if (A[i] > largest) {
largest = A[i];
}
}
return largest;
}
static int[] makeRandomArray (int length)
{
int[] A = new int [length];
for (int i=0; i < A.length; i++) {
A[i] = UniformRandom.uniform (1, 100);
}
return A;
}
}
In-Class Exercise 1:
Download the above program
(You'll also need UniformRandom.java)
and modify it to also print the positions in the array where
the min and max occur. For example,
Smallest=24 at position=1, largest=87 at position=8 in array [51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
Let's examine a variation of the program written for
String's:
import java.util.*;
public class FindStringExtremes {
public static void main (String[] argv)
{
// Some test data (a subset of Java's reserved words).
String[] reservedWords = {"if", "else", "while", "do", "return",
"true", "false", "instanceof", "class"};
// Here, smallest means 'alphabetically first'.
String smallest = findSmallest (reservedWords);
String largest = findLargest (reservedWords);
// Print.
System.out.println ("Smallest=\"" + smallest + "\", largest=\"" + largest + "\" in array " + Arrays.toString(reservedWords));
}
static String findLargest (String[] words)
{
String largest = words[0];
for (int i=1; i < words.length; i++) {
// Note: compareTo() method in String returns an int.
if ( words[i].compareTo (largest) > 0 ) {
largest = words[i];
}
}
return largest;
}
static String findSmallest (String[] words)
{
String smallest = words[0];
for (int i=1; i < words.length; i++) {
if ( words[i].compareTo (smallest) < 0 ) {
smallest = words[i];
}
}
return smallest;
}
}
Note:
- The class String has a compareTo() method
that when invoked as str1.compareTo(str2)
returns -1 if str1
comes alphabetically before str2
returns 1 if str1
comes alphabetically after str2
returns 0 if the two strings are equal
- In all other respects, the program is like the one for
integer arrays.
Next, let's return to the integer example and:
- Find the smallest element.
- Then place the smallest element in the first position in the
array.
- Whatever was in the first position gets moved to where the
smallest one was found.
Here's the program:
import java.util.*;
public class SmallestInFront {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
smallestInFront (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void smallestInFront (int[] A)
{
// Start by assuming first is smallest.
int smallest = A[0];
// We're going to record the position where the smallest occurs.
int pos = 0;
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in front.
int temp = A[0];
A[0] = A[pos];
A[pos] = temp;
}
static int[] makeRandomArray (int length)
{
// ... same as before ...
}
}
In-Class Exercise 2:
Modify the above idea to put the largest element at the back
(last position) of the array, and do this for String arrays.
Download LargestAtBack.java and
implement the method largestAtBack().
Now let's examine a small variation: we'll place the smallest
two elements at the front:
import java.util.*;
public class SmallestInFront2 {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
smallestTwoInFront (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void smallestTwoInFront (int[] A)
{
// First, the smallest in front.
int smallest = A[0];
int pos = 0;
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in front.
int temp = A[0];
A[0] = A[pos];
A[pos] = temp;
// Now for the second smallest: put that in A[1].
smallest = A[1];
pos = 1;
// Check against A[2], A[3] ... etc.
for (int i=2; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in A[1].
temp = A[1];
A[1] = A[pos];
A[pos] = temp;
}
static int[] makeRandomArray (int length)
{
// ... same as before ...
}
}
In-Class Exercise 3:
Here's some sample output for the above program:
Before: [51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
After: [24, 32, 63, 73, 42, 85, 71, 41, 87, 51]
Explain how '51' reached the last position in the array.
We'll now extend this idea to create our first sorting algorithm.
Selection sort
The idea behind Selection Sort is simple:
- Find the smallest element and put that in the first array position.
- Find the second smallest, and put that in the second position.
- Find the third smallest, ... etc.

Take the Clubs out of your deck to make a smaller deck of Clubs only, shuffle up the Club deck to randomize the order, and then follow along with the algorithm to understand how it works!
- Each pass through the deck, we need to find the smallest unsorted card and "select" it.
- We don't know what the smallest value is until we have looked at the entire deck.
- Assuming we have not lost a card the smallest card for the first pass would be the Ace of Clubs.
- Once we reach the end of the dek, we are sure that we have found the smallest value, so swap that selected card with the card at the front of the deck.
- Starting with the second card in the deck, find the smallest value of the remaining cards and select it. We can ignore the first value, we just sorted it!
- For this pass, this would be the Two of Clubs, but again we don't know that this is the smallest value until we have looked at every card in the deck.
- We swap the selected card, i.e. the second smallest card, with the card in the second position in the deck.
- Repeat this process for all of the other values, and the deck will be sorted!
Remember that a computer can only do one thing at a time, i.e. look at an individual card or compare one card with one other, so don't imagine that you can just jump to the end when a computer must go through each position to examine or compare cards.
Here's the program:
import java.util.*;
public class SelectionSort {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
selectionSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void selectionSort (int[] A)
{
// We don't need to find the n-th smallest, so stop at n-1.
for (int i=0; i < A.length-1; i++) {
// Find i-th smallest and swap.
int smallest = A[i];
int pos = i;
// Look from i+1 and up.
for (int j=i+1; j < A.length; j++) {
if (A[j] < smallest) {
smallest = A[j];
pos = j;
}
}
// Swap into position i.
int temp = A[i];
A[i] = A[pos];
A[pos] = temp;
}
}
static int[] makeRandomArray (int length)
{
// ...
}
}
In-Class Exercise 4:
Download the above program
and modify it so that the largest element
is placed at the back, then the second largest is placed in the
second-last position in the array, ... and so on.
Bubble sort
Bubble Sort iterates through a whole list of values and compares neighbors. If two neighbors are out of order, it swaps to two values. If it reaches the end of the list, bubble sort starts over and repeats the process if there was a swap. If bubble sort reaches the end of the list and does not perform a swap, the list must be in order. It is called Bubble Sort because smaller values (or larger values depending on the particular impelmentation) will bubble to the front of the list quickly.

Let's use a different suit of cards say Diamonds. Shuffle the deck of Diamonds to randomize the order, and follow along with the algorithm to see how it works!
- Lay your cards out in a row.
- Start from the left side of the row.
- Compare the leftmost pair of cards in the row to one another.
- If the left card of the pair has a larger value than the right card of the pair, swap the two cards.
- Compare the second pair of cards. This will be the second and third cards from the left which will include one card that you just compared.
- If the left card of the pair has a larger value than the right card of the pair, swap the two cards.
- Repeat this process for all neighboring pairs in the row moving from left to right until you reach the end of the row.
- Once you reach the end of the row, if you swapped any neighbors, go back to the leftmost card and start the process over again. If you did not swap any neighbors, the row is in order and you are finished!
The key ideas behind Bubble Sort:
- Bubble-sort performs several sweeps starting from the end
of the array.
- In each sweep, we swap neighboring elements out of order.
- If we perform enough sweeps, the array will end up sorted.
Let's look at the code:
import java.util.*;
public class BubbleSort {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
bubbleSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void bubbleSort (int[] A)
{
// Each sweep, i=0...n-1, will put the i-th least element in place.
for (int i=0; i < A.length-1; i++) {
// Perform swaps from end-of-array down to i-th position.
for (int j=A.length-1; j>i; j--) {
if (A[j] < A[j-1]) {
// Out of order: swap needed.
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
}
static int[] makeRandomArray (int length)
{
// ...
}
}
To see how it works in a little more detail,
let's sort the
array [40, 30, 10, 50, 20]:
Sweep for i=0:
Comparison at position j=4: 40 30 10 50 20 // Need to swap 20 and 50
Comparison at position j=3: 40 30 10 20 50
Comparison at position j=2: 40 30 10 20 50 // Need to swap 10 and 30
Comparison at position j=1: 40 10 30 20 50 // Need to swap 10 and 40
Sweep for i=1:
Comparison at position j=4: 10 40 30 20 50
Comparison at position j=3: 10 40 30 20 50 // Need to swap 20 and 30
Comparison at position j=2: 10 40 20 30 50 // Need to swap 20 and 40
Sweep for i=2:
Comparison at position j=4: 10 20 40 30 50
Comparison at position j=3: 10 20 40 30 50 // Need to swap 30 and 40
Sweep for i=3:
Comparison at position j=4: 10 20 30 40 50
Insertion sort
Insertion Sort iterates through the list of values and sorts each value by placing the value into its proper position. It sounds complicated, but it is really just a variation on bubble sort.

For this case, use the Hearts from your deck, shuffle to randomize the order, and follow along with the algorithm to see how it works!
- Lay your cards out in a row.
- Start from the left side of the row.
- Ignore the first card for now.
- Focus on the card in the second position from the left...
- Compare the second card with the first card...
- If the left card of the pair has a larger value than the right card of the pair, swap the two cards. (This is the "insertion")
- Note that among these two cards only, they are now sorted.
- Focus on the third position...
- Compare the third card with the second card.
- If the left (second) card is larger than the right (third) card, swap the two cards.
- If no swap was needed, all three cards are sorted.
- If a swap was needed, then repeat this process with all preceding neighbors until the card lands in its sorted position.
- Continue this process for the remaining cards in the fourth through last positions.
- Once the last card has been inserted (using the bubble sorting strategy) into its correct position, the row will be sorted.
We'll lead up to Insertion-Sort through a couple
of examples.
First, consider this idea:
- We'll create a separate array that will contain the sorted elements.
- To create the sorted array, we go through the original and
copy over the current element "into the right place" in the sorted array.
- For example, suppose array A is to be sorted:
- We'll created a sorted version in array B.
- Here are the first few elements when we start:
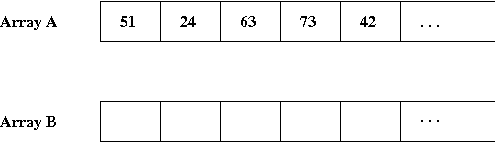
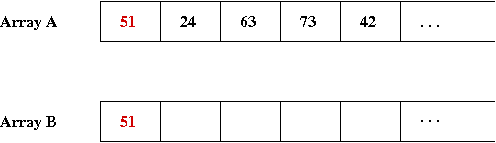
- The first element to insert in B is '51', which gets
into the first spot in B:
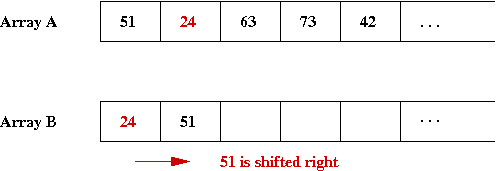
- Next element to insert is '24', for which we need to shift
'51' in the B array
⇒ We'll keep B sorted.
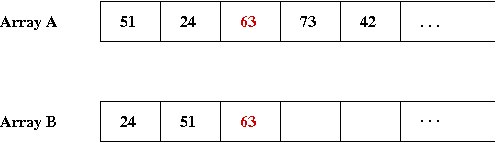
- Next element is '63', which goes into the 3rd spot:
- Then '73':
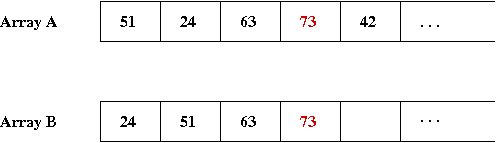
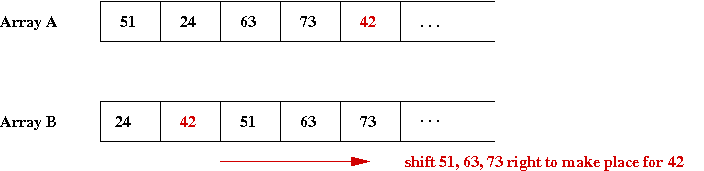
- Finally, for '42', we need to shift-right three elements to
find the right place for '42':
- Thus, the general idea is:
- Proceed sequentially through A's elements.
- For each, find the right place in B, shifting right
as necessary.
Here's the program:
import java.util.*;
public class InsertionSort1 {
public static void main (String[] argv)
{
int[] testData = {51, 24, 63, 73, 42, 85, 71, 41, 87, 32};
System.out.println ("Before: " + Arrays.toString(testData));
int[] sortedData = insertionSort (testData);
System.out.println ("After: " + Arrays.toString(sortedData));
}
static int[] insertionSort (int[] A)
{
// Make space for the "result" array B:
int[] B = new int [A.length];
// Go through A's elements and find the right place for each in B:
for (int i=0; i < A.length; i++) {
// Find the right place for A[i] in array B.
int posInB = i;
for (int j=0; j < i; j++) {
if (B[j] < A[i]) {
// Skip.
}
else {
posInB = j;
break;
}
}
// Now shift rightwards in B from posInB onwards.
for (int j=i+1; j>posInB; j--) {
// We need this because the array has to be shifted except
// for the last position when i=n-1.
if (j < B.length) {
B[j] = B[j-1];
}
}
// Assign A[i] in right place.
B[posInB] = A[i];
}
return B;
}
static int[] makeRandomArray (int length)
{
// ...
}
}
Note:
- To find the right place in B:
- We start at the right end of B (the most recent
index is i.
- We scan backwards, going past all elements that are larger
than A[i].
- When we find the right place:
- We shift-right all elements we skipped over.
- Then we insert A[i].
Now for the first clever insight:
- When we scan backwards in B, we can combine that
with shifting right
⇒
This is because we the elements we skip over need to be shifted right.
Let's re-write insertionSort() to do that:
static int[] insertionSort (int[] A)
{
int[] B = new int [A.length];
for (int i=0; i < A.length; i++) {
B[i] = A[i];
// Start at rightmost element in B.
int j = i;
// Swap as we go backwards.
while ( (j > 0) && (B[j] < B[j-1]) ) {
int temp = B[j];
B[j] = B[j-1];
B[j-1] = temp;
j --; // Mustn't forget the decrement.
}
}
return B;
}
Now the really clever insight:
- We don't need a separate array at all!
- After all, those elements we are skipping/swapping are precisely
those "to the left" in B
⇒
But these are the same "to-the-left" elements in A!
Here's a re-write of insertionSort() using only array A:
static void insertionSort (int[] A)
{
for (int i=0; i < A.length; i++) {
// Find the right place for A[i].
int j = i;
while ( (j > 0) && (A[j] < A[j-1]) ) {
// Swap until we stop.
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
j --;
}
}
}
Finally, we point out that a for-loop could be used instead
of the while-loop:
static void insertionSort (int[] A)
{
for (int i=0; i < A.length; i++) {
for (int j=i; (j>0) && (A[j] < A[j-1]); j--) {
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
In-Class Exercise 5:
Modify each of
SelectionSort.java,
BubbleSort.java
and
InsertionSort.java
to count the total number of comparisons made. That is:
- Each time two elements are compared for their "size", count
that as one comparison.
- Modify each file separately.
- Print the total number of comparisons required for
SelectionSort, the total required for BubbleSort and the
total required for InsertionSort.
Get this working for an array size of 10 elements. Then, get
the number-of-comparisons for a 20-element array, then 30, ...,
until 100. Plot a graph (by hand, on paper)
of the number of comparisons vs. array size.
Sorting our own objects
Let's look at an example where we create objects of our own design and
sort them:
Here's the program:
class Person {
// Some data:
String firstName;
String lastName;
int birthYear;
// This is called a constructor:
public Person (String firstName, String lastName, int birthYear)
{
this.firstName = firstName;
this.lastName = lastName;
this.birthYear = birthYear;
}
// A comparison method to allow two Person instances to be compared.
public boolean lessThan (Person p)
{
// Compare the birthyear inside this instance (where we are executing)
// with the birthyear of the parameter instance.
if (birthYear < p.birthYear) {
return true;
}
else {
return false;
}
}
} // end-of-Person
public class ObjectSortExample {
public static void main (String[] argv)
{
// Make space for 10 person pointers.
Person[] someKennedys = new Person [10];
// Each array location is itself an object pointer. We
// need to assign actual object instances using the new operator.
someKennedys[0] = new Person ("Patrick", "Kennedy", 1858);
someKennedys[1] = new Person ("Joseph", "Kennedy", 1888);
someKennedys[2] = new Person ("Rose", "Fitzgerald", 1890);
someKennedys[3] = new Person ("Joseph", "Kennedy", 1915);
someKennedys[4] = new Person ("John", "Kennedy", 1917);
someKennedys[5] = new Person ("Jacqueline", "Bouvier", 1929);
someKennedys[6] = new Person ("Robert", "Kennedy", 1925);
someKennedys[7] = new Person ("Edward", "Kennedy", 1932);
someKennedys[8] = new Person ("Caroline", "Kennedy", 1957);
someKennedys[9] = new Person ("Maria", "Shriver", 1955);
System.out.println ("Unsorted: ");
print (someKennedys);
sort (someKennedys);
System.out.println ("\nSorted: ");
print (someKennedys);
}
static void print (Person[] people)
{
for (int i=0; i < people.length; i++) {
System.out.println (people[i].firstName + " " + people[i].lastName + " (b. " + people[i].birthYear + ")");
}
}
static void sort (Person[] people)
{
// Selection Sort.
for (int i=0; i < people.length-1; i++) {
Person min = people[i];
int pos = i;
for (int j=i+1; j < people.length; j++) {
// Compare j-th person with best so far.
if ( people[j].lessThan (min) ) {
min = people[j];
pos = j;
}
}
// Swap.
Person temp = people[i];
people[i] = people[pos];
people[pos] = temp;
}
}
} // end-of-ObjectSortExample
Note:
- In the int version of Selection-Sort, the key
comparison occured in the for-loop:
for (int j=i+1; j < A.length; j++) {
if (A[j] < smallest) {
smallest = A[j];
pos = j;
}
}
Here, A[i] (an int) is compared to
smallest (also an int).
- In the Person example,
for (int j=i+1; j < people.length; j++) {
if ( people[j].lessThan (min) ) {
min = people[j];
pos = j;
}
}
Here, people[j] (a Person instance) is
compared to min (also a Person instance).
- The comparison itself is done inside the method
lessThan() in one instance.
Quicksort
Quicksort uses a novel strategy unlike any of the other sorts discussed so far. Quicksort relies on subdividing the set into two smaller sets that each represent a step toward the complete solution. By dividing the data in half, and moving closer to a solution in both halves, more progress is made in one pass of the data than is made by the other sort examples discussed in this module.

Take the Spades out of your deck to make a smaller deck of Spades only, shuffle to randomize the order, and follow along with the algorithm to see how it works!
- Look at the first card in the Heart pile
- If the card is 7 or less, place the card in a new small card pile to the left.
- If the card is 8 or more, place the card in a new big card pile to the right.
- Repeat this process for all cards in the Heart pile
- Look at the first card in the small card pile
- If the card is 3 or less, place the card in a new smallest cards pile.
- If the card is 4 or more, place the card in a new middle cards pile
- Repeat this process for all cards in the small card pile
- Look at the first card in the smallest card pile
- If the card is less than 2 (the Ace) place it to the left
- If the card is 2 or more (2 or 3) place it to the right
- Repeat this process for all cards in the smallest card pile
- The left-most pile (the Ace) is sorted, because a pile of one card is always sorted.
- Look at the right pile from the smallest cards. There are only two cards here: the 2 and the 3. If they are out of order, swap them.
- Combine these two piles back into on pile by placing the left pile on top of the right pile. These three cards should now be sorted.
- Repeat this process on the "middle" cards then place the stack of the "smallest" cards back on top of the "middle" cards. These 7 cards should now be sorted.
- Repeat the same process on the cards that are greater than 8. Once you recombine the small cards and the big cards you will have sorted all the Hearts.
You can easily extend the above exercise to the entire deck. Here are the first few steps when sorting the deck as a whole:
- Look at the first card to determine the color of it's suit.
- If the card is a red suit, place the card in a pile to the left
- If the card is a black suit, place the card in a pile to the right.
- Repeat this process for all cards in your deck until all cards are either in the red pile or the black pile.
- Look at the first card in the black pile
- If the card is a Spade, place the card in a new pile to the left.
- If the card is a Club, place the card in a new pile to the right.
- Repeat this process for all cards in the black pile until all black cards are either in the Spade pile or the Club pile. For the red cards, divide them based on whether they are a Heart or a Diamond.
- Use the same process as sorting the Spades above to sort each individual suit
Key ideas in Quicksort:
- Consider the array
[51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
and the first element '51'.
- Suppose we place the elements less than '51' to the left
and those greater to the right of it:
[24, 42, 41, 32] 51 [63, 73, 85, 71, 87]
- Then, suppose we magically sort the left array independently:
[24, 32, 41, 42] 51 [63, 73, 85, 71, 87]
- Next, suppose we magically sort the right array:
[24, 32, 41, 42] 51 [63, 71, 73, 85, 87]
- Then, we can piece together the final result:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- Key insight: sorting the smaller arrays (left and right)
is just like sorting a larger array
⇒
We can apply the same idea recursively.
- Thus, the code is going to look like this:
static void quickSortRecursive (int[] data, int left, int right)
{
if (left < right) {
// Partition to find the "right place" for the leftmost element.
int partitionPosition = quickSortPartition (data, left, right);
// Recurse on the left side:
quickSortRecursive (data, left, partitionPosition-1);
// Recurse on the right side:
quickSortRecursive (data, partitionPosition+1, right);
}
// Else: left==right so we're done.
}
- We won't need to build separate arrays if we can somehow
do everything in one array:
- When we "partition" the array, we use the leftmost element
and find the "right place" for it:
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^
partition position = 4
- Then, all we need are the limits on each side:
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^ ^ // Left array limits
left=0 right=3
and
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^ ^ // Right array limits
left=6 right=9
- Thus, if we can write the recursive method to work with "left"
and "right" indices to delineate a portion of the array, we can use
the same array.
Here's the program:
import java.util.*;
public class QuickSort {
public static void main (String[] argv)
{
int[] testData = {51, 24, 63, 73, 42, 85, 71, 41, 87, 32};
System.out.println ("Before: " + Arrays.toString(testData));
quickSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void quickSort (int[] A)
{
quickSortRecursive (A, 0, A.length-1);
}
static void quickSortRecursive (int[] data, int left, int right)
{
if (left < right) {
// Partition to find the "right place" for the leftmost element.
int partitionPosition = quickSortPartition (data, left, right);
// Recurse on the left side:
quickSortRecursive (data, left, partitionPosition-1);
// Recurse on the right side:
quickSortRecursive (data, partitionPosition+1, right);
}
// Else: left==right so we're done.
}
static int quickSortPartition (int[] data, int left, int right)
{
if (left == right)
return left;
int partitionElement = data[right];
int currentSwapPosition = right;
for (int i=right-1; i>=left; i--) {
// Examine everything between left and right-1 inclusive.
if (data[i] > partitionElement) {
// Switch with swap position
currentSwapPosition--;
swap (data, currentSwapPosition, i);
// Shift swap position rightwards:
}
}
// Last one:
swap (data, currentSwapPosition, right);
return currentSwapPosition;
}
static void swap (int[] data, int i, int j)
{
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
In-Class Exercise 6:
Can you identify where in the code comparisons are actually made?
Modify QuickSort2.java to count the
number of comparisons. Then plot the results along with the
other sort algorithms in Exercise 5 above.
Brute Force and Divide and Conquer
Selection, Bubble, and Insertion Sorts belong to a class of algorithms that employ a brute force strategy. A brute force strategy is typically based on an iterative approach that repeatedly operates on the same data. A brute force strategy will typically focus on solving the smallest part of the problem in one step and then repeat those steps over and over until it reaches an overall solution.
Quicksort belongs to a class of algorithm that employ a divide-and-conquer strategy. A divide-and-conquer strategy is typically based on subdividing the problem into smaller and smaller problems where each subdivision represents a partial solution. By subdividing, the size of the problem is reduced down to a point where the problem can no be subdivided again. Once this discrete solution level is reached, the complete solution is assembled from all the solutions to the subproblems. This class of algorithms can be solved iteratively, but due to the nature of the approach, can also be typically solved using a recursive implementation.
Measuring actual run time
In Java, it is fairly easy to measure actual running time, accurate
to within milliseconds, for example:
// Get the current time (in milliseconds).
long startTime = System.currentTimeMillis ();
// Here's the code we're going to evaluate.
selectionSort (A);
// After it has run, we record the time taken as the current
// time minus the starttime.
long timeTaken = System.currentTimeMillis () - startTime;
System.out.println ("Selection sort time: " + timeTaken);
In-Class Exercise 7:
Download and execute SortPerformance.java
to compare QuickSort with SelectionSort.
Do either InsertionSort or BubbleSort compare with QuickSort?
Copy over those algorithms and try it out.
© 2006-2021, Rahul Simha & James Taylor (revised 2021)







