Module 10: Trees and Hash Tables
Supplemental material
Access speed: an example
We'll use a simple application to demonstrate that trees can be
much faster than lists:
- The application: count the number of English words whose
reversals are also words.
⇒
These include palindromes like
"rotor" as well as words like "regal" or "edit".
- Our simple algorithm for this purpose is going to be:
1. for each word w
2. w' = reverse (w)
3. if w' is a word
4. count = count + 1
5. endif
6. endfor
7. return count
- In line 3 above, how do we tell whether a string so
generated is a word?
⇒
Check whether the string is in the dictionary.
- We will use a data structure for this purpose.
- With this additional detail, the pseudocode is now:
// Build the data structure and put all the words in it.
1. DS = create new data structure
2. for each word w
3. add w to DS
4. endfor
// Now check each possible reversal.
5. for each word w
2. w' = reverse (w)
3. if DS.contains (w')
4. count = count + 1
5. endif
6. endfor
7. return count
In-Class Exercise 1:
If we used a linked list and if the number of words in n,
how long (order-notation) does the above algorithm take?
Next, let's use Java's tree data structure and compare:
- We will record the actual time taken for each of three
data structures:
- A tree.
- A linked-list.
- An array-list.
Here's the program:
import java.util.*;
public class WordReversals {
public static void main (String[] argv)
{
// Fetch the dictionary.
String[] words = WordTool.getDictionary ();
// Compare a tree data structure with ArrayList and LinkedList.
findReversalsUsingTree (words);
findReversalsUsingArrayList (words);
findReversalsUsingLinkedList (words);
}
static void findReversalsUsingTree (String[] words)
{
long startTime = System.currentTimeMillis();
// Count such words.
int count = 0;
// First put all words into a tree.
TreeSet wordSet = new TreeSet ();
for (int i=0; i < words.length; i++) {
wordSet.add (words[i]);
}
// Now perform the search for reversals.
for (int i=0; i < words.length; i++) {
String reverseStr = reverse (words[i]);
if (wordSet.contains (reverseStr)) {
count ++;
System.out.println (words[i]);
}
}
// How much time has elapsed?
long timeTaken = System.currentTimeMillis() - startTime;
System.out.println ("Using a tree: count=" + count + " timeTaken=" + timeTaken);
}
static void findReversalsUsingArrayList (String[] words)
{
// ... similar except that we use an ArrayList ...
}
static void findReversalsUsingLinkedList (String[] words)
{
// ... similar except that we use a LinkedList ...
}
static String reverse (String str)
{
// ... Reverse a string. This method is used above.
}
}
In-Class Exercise 2:
Download WordReversals.java,
compile and execute to see the difference in performance.
Next, just like TreeSet is used above, write code
that uses a HashSet (which is also in the Java libary)
and compare performance. Which was the fastest data structure?
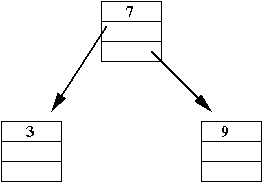
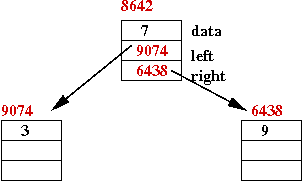
Nodes with multiple pointers
Recall from linked lists:
- Each node in a linked list has a next pointer.
class ListItem {
String data; // The data to be stored.
ListItem next; // A pointer to the next node in the list.
}
- A doubly-linked list has two pointers:
class ListItem {
String data; // The data to be stored.
ListItem next; // A pointer to the next node in the list.
ListItem prev; // Points to previous item in list.
}
Consider this program that builds a linked structure:
class Node {
String data; // The data to be stored.
Node left; // Two pointers.
Node right;
}
public class StrangeStructure {
public static void main (String[] argv)
{
// Step 1:
Node root = new Node ();
root.data = "Ewok";
// Step 2:
root.right = new Node ();
root.right.data = "Gungan";
// Step 3:
root.left = new Node ();
root.left.data = "Aqualish";
// Step 4:
root.left.left = new Node ();
root.left.left.data = "Amanin";
// Step 5:
root.left.right = new Node ();
root.left.right.data = "Cerean";
}
}
In-Class Exercise 3:
Draw the memory picture after each of the five steps above.
Download StrangeStructure.java.
Then modify the code to
add the string "Jawa" to the right of the "Gungan" node,
and then add the string "Hutt" to the left of the "Jawa" node you just added.
Draw the memory picture on paper.
Can you find a tribe to add to the left of "Gungan" and another one
to add to the right of "Jawa"?
Binary trees
We'll start our discussion of trees by looking at some simple
examples:
- Before we get to trees, consider the idea of order in
a data structure:
- This is an unordered list:

- This is an ordered list:

- Note: an ordered list is unique if the values are unique.
- In the same sense, this is an unordered binary tree:
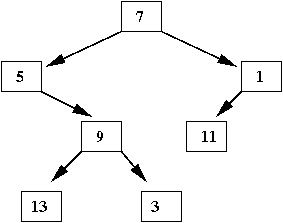
- In a binary tree, each node has two pointers: to a left
child and to a right child.
- Sometimes, a pointer is null (e.g., no left child)
⇒
For example, node 5 above has no left child and node 1 has no
right child.
- Notice that every node is itself the root of a subtree
that's a binary tree.
⇒
This is true if we allow a single node to be considered a tree.
- The same values in an ordered binary tree:
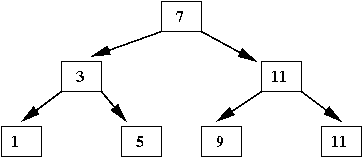
- For every node, all the values in the subtree to the left
are smaller than it.
- For every node, all the values in the right subtree are larger.
- Example: The values in the left subtree of 7 are: 3, 1 5
- Example: The values in the right subtree of 11 are: 13
- There is no unique binary tree
⇒
For example, this is another binary tree with the same values:
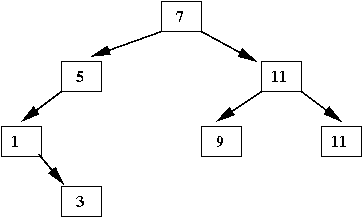
In-Class Exercise 4:
Draw yet another (ordered) binary tree with the same values, this time
with 9 as root (instead of 7). There are many such possibilities; you
need only draw one of them.
Henceforth, we will be interested only in ordered binary trees.
Search in a binary tree:
- To search for an element (e.g., 11 in the tree above), compare
with the current node:
⇒
If the element is smaller than the node's value, explore the
left subtree, otherwise the right.
- In high-level pseudocode:
1. Start with the root.
2. if the given value is equal to the current node's value
3. return found
4. elseif given value < node's value
5. explore left subtree (recursively)
6. else
7. explore right subtree (recursively)
8. endif
- Let's make the pseudocode a little more precise:
Algorithm: recursiveSearch (node, element)
// Check to see if the given element is in the node we're examining.
1. if element = node.value
2. return found
3. endif
// Otherwise, search the appropriate subtree (left or right)
4. if element < node.value
5. return recursiveSearch (node.left, element)
6. else
7. return recursiveSearch (node.right, element)
8. endif
In-Class Exercise 5:
Explore the steps in searching for "5" in this tree:

Then, explore the steps in searching for "4" in the same tree.
Where does the latter search end?
Insertion of new elements:
- The key idea is:
- Do a search and see where it ends.
- Insert where the search ends.
- Example: we will insert the following values: 7, 9, 3, 5, 1,
11, 13 (in that order)
- When we insert '7'
- The tree is initially empty
⇒
We create a new root.
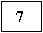
- Next, insert '9'
- '9' is larger than '7', so we look in the right subtree
⇒
It's empty, so we stop there and insert '9' as the right-child of '7'
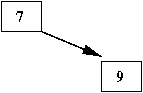
- Next, insert '3'
- '3' is smaller than '7', so we look in the left subtree
⇒
It's empty, so we stop there and insert '3' as the left-child of '7'
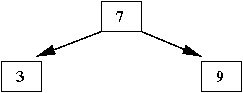
- Next, insert '5'
- A search for '5' ends at the right subtree of '3' (which is empty)
⇒
That is where we insert '5', as the right child of '3'
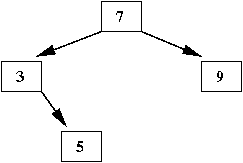
- Next, insert '1'
- A search for '1' ends at the left subtree of '3' (which is empty)
⇒
That is where we insert '1', as the left child of '3'
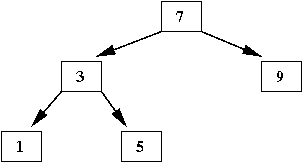
- Next, insert '11'
⇒
As a right child of '9'
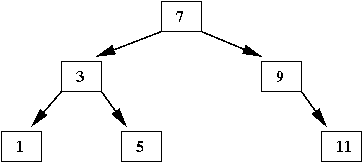
- Finally, when we insert '13'
⇒
The search ends in the right subtree of '11'
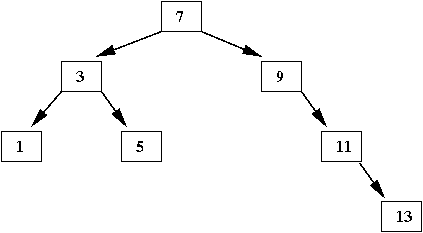
In-Class Exercise 6:
If '10' were inserted into the above tree, where would it be placed?
In-Class Exercise 7:
Insert the values 5, 9, 1, 3, 7, 13, 11 (in that order) into a binary tree.
Let's now look at implementation:
Here's the program:
import java.util.*;
// Each node of the tree is an instance of the class TreeNode.
class TreeNode {
int data;
TreeNode left; // Pointer to the left child.
TreeNode right; // Pointer to the right child.
}
public class BinaryTreeInt {
TreeNode root = null; // Root of the tree.
int numItems = 0; // We'll keep track of how many elements we've added so far.
public void add (int k)
{
// If empty, create new root.
if (root == null) {
root = new TreeNode (); // Note: root.left and root.right are initialized to null
root.data = k;
numItems ++;
return;
}
// Search to see if it's already there.
if ( contains (k) ) {
// Handle duplicates.
return;
}
// If this is a new piece of data, insert into tree.
recursiveInsert (root, k);
numItems ++;
}
void recursiveInsert (TreeNode node, int k)
{
// Compare input data with data in current node.
if (k < node.data) {
// It's less. Go left if possible, otherwise we've found the correct place to insert.
if (node.left != null) {
recursiveInsert (node.left, k);
}
else {
node.left = new TreeNode ();
node.left.data = k;
}
}
// Otherwise, go right.
else {
// It's greater. Go right if possible, otherwise we've found the correct place to insert.
if (node.right != null) {
recursiveInsert (node.right, k);
}
else {
node.right = new TreeNode ();
node.right.data = k;
}
}
}
public int size ()
{
return numItems;
}
public boolean contains (int k)
{
if (numItems == 0) {
return false;
}
return recursiveSearch (root, k);
}
boolean recursiveSearch (TreeNode node, int k)
{
// If input string is at current node, it's in the tree.
if (k == node.data) {
// Found.
return true;
}
// Otherwise, navigate further.
if (k < node.data) {
// Go left if possible, otherwise it's not in the tree.
if (node.left == null) {
return false;
}
else {
return recursiveSearch (node.left, k);
}
}
else {
// Go right if possible, otherwise it's not in the tree.
if (node.right == null) {
return false;
}
else {
return recursiveSearch (node.right, k);
}
}
}
}
In-Class Exercise 8:
Download BinaryTreeInt.java
and BinaryTreeIntExample.java
and modify the latter file to insert the elements
5, 9, 1, 3, 7, 13, 11 (in that order) into a new binary tree.
- Draw a detailed memory-picture with the resulting tree.
- You will notice a method called print(). What does it
do? Why does it have a queue? Can you make sense of the output?
In-Class Exercise 9:
Implement a recursive print method. The template for this
is already in the above code (see Exercise 8 above).
An example with strings
What do we need to change to create a binary tree for strings?
- Not much, as it turns out:
- The tree node needs to have the data type changed:
class TreeNode {
String data; // Changed from int to String
TreeNode left;
TreeNode right;
// ...
}
- The methods add() and contains() have a
signature for strings:
public class BinaryTreeString {
public void add (String data)
{
// ...
}
public boolean contains (String str)
{
// ...
}
}
- Comparisons with String's need to use the
compareTo() in the class String:
public class BinaryTreeString {
public void add (String data)
{
// ...
}
public boolean contains (String str)
{
if (numItems == 0) {
return false;
}
return recursiveSearch (root, str);
}
boolean recursiveSearch (TreeNode node, String str)
{
if ( str.compareTo (node.data) == 0 ) {
// Found.
return true;
}
// Otherwise, navigate further.
if ( str.compareTo (node.data) < 0 ) {
// Go left if possible, otherwise it's not in the tree.
if (node.left == null) {
return false;
}
else {
return recursiveSearch (node.left, str);
}
}
else {
// Go right if possible.
// ... similar to above ...
}
}
}
In-Class Exercise 10:
Download BinaryTreeString.java
and BinaryTreeStringExample.java.
Then compile and execute. You will see that seven strings have been
inserted.
- Draw the tree that results.
- Find an appropriate string to add as a left child of "Gungan".
- Examine the code and study the methods that implement
pre-order printing and in-order printing.
- What is the effect of in-order printing?
- Implement post-order printing.
Analysis
Let us compare search in lists vs. trees:
- In a list, search (contains()) takes
O(n) time (worst-case).
- In a tree?
- First, nomenclature: a leaf of a tree is a node
with no children.
- A search, worst-case, can take us down the longest path from
the root to a leaf node.
- However, it's not clear how long such a path could be.
- Definition: the height (or depth) of a
binary tree is the length of the longest path from the root to a leaf.
In-Class Exercise 11:
Suppose we insert the numbers 1, 2, ..., 10 into a binary tree in that order.
Draw the resulting binary tree.
What is the height of the tree?
The height of a full tree:
- In a full tree, all the leaves are at the same level.
In-Class Exercise 12:
Draw a full tree of height 1. Then draw a full tree of height 2.
In fact, draw full trees of heights 3 and 4, after that.
Count the number of nodes in each tree.
- If a full tree has height h, how many nodes does the tree have?
- If a full tree has n nodes, what is the height in terms
of n?
Balanced trees:
- In a balanced binary tree, no two leaves have a significantly
different path length to the root.
- Usually, path-lengths differ by at most one in some kinds of
balanced trees.
- There are many such height-balanced trees, e.g., AVL-trees, M-way trees
⇒
These are more complicated and usually covered in an Algorithms course.
Back to the analysis:
- The search time for a balanced binary tree is O(log(n)),
because the height is about O(log(n)) for a tree with
n nodes.
- Insertion also takes O(log(n)) time.
- Thus balanced binary trees are significantly faster than lists.
- What about un-balanced (regular) binary trees?
- If elements are inserted in random order, there's a good
chance that it will be balanced.
- Here's a summary of performance for the data structures
we've seen so far:
| Data structure | Insertion | Search |
| LinkedList | O(1) | O(n) |
| ArrayList | O(n)? | O(n) |
| SortedList | O(n) | O(log(n)) |
BinaryTree
(balanced) | O(log(n)) | O(log(n)) |
In-Class Exercise 13:
Why is there a question mark next to the insertion-time for ArrayList?
Why is the search time for a sorted-list O(log(n))?
The Map ADT
About the Map ADT:
- The term map is used to denote a relationship, as in "this string maps
to that integer".
- Recall the set ADT:
public class BinaryTree {
public void add (String data)
{
// ...
}
public boolean contains (String str)
{
// ...
}
}
This data structure stores strings
⇒
It represents a set of strings.
- A map version would look like:
public class BinaryTree {
public void set (String key, Object value)
{
// ...
}
public boolean contains (String key)
{
// ...
}
public Object get (String key)
{
// ...
}
}
Thus, there are three operations:
- set(): to add or update a key-value pair.
- contains(): to see if a given key is in
the data structure.
- get(): to retrieve the value associated with
the given key.
- A map thus stores associations between keys and values.
Consider an example:
- Suppose we want to store the following data in a patient
database: patient-name, age, height, weight, blood-type
- This might be a sample set of data records:
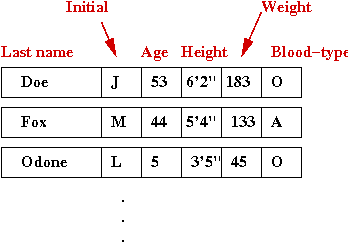
- What we'd like to do is associate a key with each record
⇒
Usually, this is what we'd use to search for the record.
- Let's use name as the key:
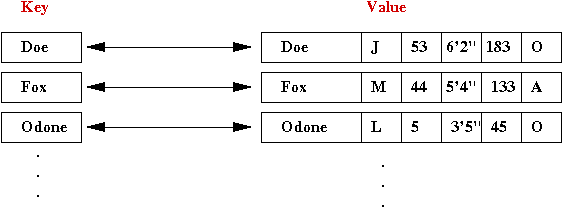
- The name becomes the key, while the entire record
becomes the associated value
⇒
A map is a data structure that stores name-value associations.
An example with trees:
- Suppose we wish to store the following associations:
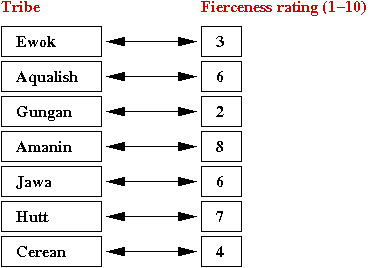
- In a program, this is how we'd like to make the
associations:
public class BinaryTreeMapExample {
public static void main (String[] argv)
{
// Create an instance of the map data structure.
BinaryTreeMap tree = new BinaryTreeMap ();
// Add name and fierceness-rating (1-10)
tree.set ("Ewok", 3);
tree.set ("Aqualish", 6);
tree.set ("Gungan", 2);
tree.set ("Amanin", 8);
tree.set ("Jawa", 6);
tree.set ("Hutt", 7);
tree.set ("Cerean", 4);
int rating = tree.get ("Hutt");
System.out.println ("Rating for Hutt: " + rating);
}
}
Let's examine the code for BinaryTreeMap:
import java.util.*;
class TreeNode {
String key; // The key-value pair.
int value;
TreeNode left; // The usual left-child, right-child pointers.
TreeNode right;
}
public class BinaryTreeMap {
TreeNode root = null;
int numItems = 0;
public void set (String key, int value)
{
// If empty, create new root.
if (root == null) {
root = new TreeNode ();
// Store both key and value:
root.key = key;
root.value = value;
numItems ++;
return;
}
// Search to see if it's already there.
if ( contains (key) ) {
// Handle duplicates.
return;
}
// If this is a new piece of data, insert into tree.
recursiveInsert (root, key, value);
numItems ++;
}
void recursiveInsert (TreeNode node, String key, int value)
{
// Compare input key with key in current node: comparisons are only with keys.
if ( key.compareTo (node.key) < 0 ) {
// It's less. Go left if possible, otherwise we've found the correct place to insert.
if (node.left != null) {
recursiveInsert (node.left, key, value);
}
else {
node.left = new TreeNode ();
node.left.key = key; // Store both key and value.
node.left.value = value;
}
}
// Otherwise, go right.
else {
// It's greater. Go right if possible, otherwise we've found the correct place to insert.
if (node.right != null) {
recursiveInsert (node.right, key, value);
}
else {
node.right = new TreeNode ();
node.right.key = key; // Store both key and value.
node.right.value = value;
}
}
}
public int size ()
{
return numItems;
}
public boolean contains (String str)
{
if (numItems == 0) {
return false;
}
TreeNode node = recursiveSearch (root, str);
if (node == null) {
return false;
}
return true;
}
public int get (String key)
{
if (numItems == 0) {
return -1;
}
TreeNode node = recursiveSearch (root, key);
if (node == null) {
return -1;
}
return node.value;
}
TreeNode recursiveSearch (TreeNode node, String key)
{
// If input key is at current node, it's in the tree.
if ( key.compareTo (node.key) == 0 ) {
// Found.
return node;
}
// Otherwise, navigate further.
if ( key.compareTo (node.key) < 0 ) {
// Go left if possible, otherwise it's not in the tree.
if (node.left == null) {
return null;
}
else {
return recursiveSearch (node.left, key);
}
}
else {
// Go right if possible, otherwise it's not in the tree.
if (node.right == null) {
return null;
}
else {
return recursiveSearch (node.right, key);
}
}
}
} //end-BinaryTreeMap
Note:
- We store both the key and its associated value at the time of
adding a key.
- The organization of the tree depends on the keys
⇒
Values play no role in searching or tree organization.
⇒
They are merely stored along with the associated keys.
- In the above example, each key is a String and each
value is an int.
Sometimes we wish to store a more complex value
⇒
An object, for instance.
- For example, suppose we wanted to store these associations:
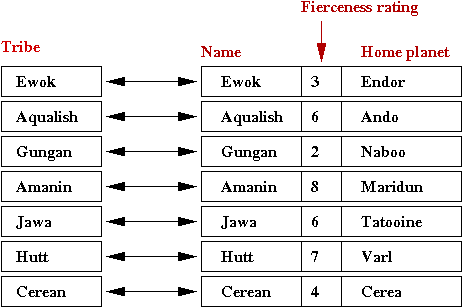
- We will use an object called TribeInfo to store the
three pieces of information:
class TribeInfo {
String name;
int fierceness;
String planet;
// Constructor.
public TribeInfo (String name, int fierceness, String planet)
{
this.name = name;
this.fierceness = fierceness;
this.planet = planet;
}
}
- Then, we'd like to create key-value associations between
tribe names and the associated object as follows:
public class BinaryTreeMapExample2 {
public static void main (String[] argv)
{
// Create an instance of our new object-version of a binary-tree map.
BinaryTreeMap2 tree = new BinaryTreeMap2 ();
// Put some key-value pairs inside.
TribeInfo info = new TribeInfo ("Ewok", 3, "Endor");
tree.set ("Ewok", info);
info = new TribeInfo ("Aqualish", 6, "Ando");
tree.set (info.name, info);
info = new TribeInfo ("Gungan", 2, "Naboo");
tree.set (info.name, info);
info = new TribeInfo ("Amanin", 8, "Maridun");
tree.set (info.name, info);
info = new TribeInfo ("Jawa", 6, "Tatooine");
tree.set (info.name, info);
info = new TribeInfo ("Hutt", 7, "Varl");
tree.set (info.name, info);
info = new TribeInfo ("Cerean", 4, "Cerea");
tree.set (info.name, info);
// Note: a cast is needed for conversion from Object to TribeInfo
// even though we know that a TribeInfo instance will be returned.
TribeInfo tInfo = (TribeInfo) tree.get ("Hutt");
System.out.println ("Info for Hutt: " + tInfo);
}
}
Let's now take a look at implementing the map:
import java.util.*;
class TreeNode {
String key;
Object value; // The value is now a generic object.
TreeNode left;
TreeNode right;
}
public class BinaryTreeMap2 {
TreeNode root = null;
int numItems = 0;
public void set (String key, Object value)
{
// ...
}
public int size ()
{
// ...
}
public boolean contains (String key)
{
// ...
}
public Object get (String key)
{
// ...
// Return value is an Object (the value)
}
}
Note:
- The code changes only slightly
⇒
The value is now of type Object.
In-Class Exercise 14:
Download BinaryTreeMapExample2.java
and BinaryTreeMap2.java.
What method should you add to TribeInfo for the printing in
main() to print something useful?
What is an Object?
- This is a special class in the Java library, and is
treated differently by the compiler.
- Every Java object is also an Object.
- Here's an example that explores the connection between
Object and any other class we define:
class MyOwnVeryObject { // A silly little object
int k;
public String toString ()
{
return ("k=" + k);
}
}
public class TestObject {
public static void main (String[] argv)
{
// Create an instance of the class defined above and set a value for one of the members.
MyOwnObject x = new MyOwnObject ();
x.k = 5;
// Invoke the toString() method:
System.out.println (x);
// Since MyOwnObject is also an Object, an Object variable can point to it.
Object obj = x;
// Invoke the toString() method: this calls the toString() method in x.
System.out.println (obj);
// Cast down from an Object variable into a MyOwnObject variable.
MyOwnObject y = (MyOwnObject) obj;
print (y);
// Casting can occur in a method call too.
print (x);
}
static void print (Object obj)
{
System.out.println (obj);
}
}
- This is why we needed the cast when we extracted
the value in the map example:
// Cast from return type (Object) into tInfo's type (TribeInfo).
TribeInfo tInfo = (TribeInfo) tree.get ("Hutt");
In-Class Exercise 15:
What would happen if we mistakenly cast into the wrong type?
Download BinaryTreeMapExample2.java
and BinaryTreeMap2.java.
Then add these lines to the end of main():
String s = (String) tree.get ("Hutt");
System.out.println ("Info for Hutt: " + s);
Why does it compile? What happens during execution? Explain.
A separate key-value pair object
An alternative to handling keys and values separately is to
create a single object that packages key-and-value:
- For example:
public class KeyValuePair {
String key;
Object value;
public KeyValuePair (String s, Object v)
{
key = s;
value = v;
}
}
- Then, our map data structure is written to work with such
objects:
import java.util.*;
class TreeNode {
KeyValuePair kvp; // A tree node now stores the Key-Value pair as an object.
TreeNode left; // The usual pointers.
TreeNode right;
}
public class BinaryTreeMap3 {
public void set (KeyValuePair kvp)
{
// ...
}
public boolean contains (String key)
{
// ...
}
public KeyValuePair get (String key)
{
// ...
}
}
Let's re-work our earlier map example to use
KeyValuePair's:
class TribeInfo {
String name;
int fierceness;
String planet;
public TribeInfo (String name, int fierceness, String planet)
{
this.name = name;
this.fierceness = fierceness;
this.planet = planet;
}
} //end-TribeInfo
public class BinaryTreeMapExample3 {
public static void main (String[] argv)
{
// Create an instance.
BinaryTreeMap3 tree = new BinaryTreeMap3 ();
// Put some key-value pairs inside.
TribeInfo info = new TribeInfo ("Ewok", 3, "Endor");
KeyValuePair kvp = new KeyValuePair ("Ewok", info);
tree.set (kvp);
info = new TribeInfo ("Aqualish", 6, "Ando");
kvp = new KeyValuePair (info.name, info);
tree.set (kvp);
// This is more compact: create the instance in the method argument list.
info = new TribeInfo ("Gungan", 2, "Naboo");
tree.set ( new KeyValuePair (info.name, info) );
info = new TribeInfo ("Amanin", 8, "Maridun");
tree.set ( new KeyValuePair (info.name, info) );
info = new TribeInfo ("Jawa", 6, "Tatooine");
tree.set ( new KeyValuePair (info.name, info) );
info = new TribeInfo ("Hutt", 7, "Varl");
tree.set ( new KeyValuePair (info.name, info) );
// A little harder to read, but even more compact:
tree.set ( new KeyValuePair ("Cerean", new TribeInfo ("Cerean", 4, "Cerea") ) );
KeyValuePair kvpResult = tree.get ("Hutt");
System.out.println ("Info for Hutt: " + kvpResult);
}
}
A linked-list map
A map can also be implemented with a linked list:
- The method signatures for the linked list would now look like this:
public class OurLinkedListMap {
public void set (KeyValuePair kvp)
{
// ...
}
public boolean contains (String key)
{
// ...
}
public KeyValuePair get (String key)
{
// ...
}
}
- Let's look at the code in contains(), for example:
public boolean contains (String key)
{
if (front == null) {
return false;
}
// Start from the front and walk down the list. If it's there,
// we'll be able to return true from inside the loop.
ListItem listPtr = front;
while (listPtr != null) {
// Note: listPtr.kvp is the KeyValuePair instance.
if ( listPtr.kvp.key.equals(key) ) {
return true;
}
listPtr = listPtr.next;
}
return false;
}
In-Class Exercise 16:
Download OurLinkedListMap.java
and LinkedListMapExample.java,
compile and execute.
Show a complete memory picture after all the elements have
been inserted.
Hashtables
Key ideas:
- Sometimes the shorter term hashing is also used.
- There are many varieties of hashtables
⇒
We will study one of the simplest: an array of linked-lists.
- Suppose we want to store the numbers: 4, 7, 8, 10, 11, 14,
23, 32, 46, 51.
- In a list, it would look like this:

- Suppose we instead store the 10 elements in 5 lists as follows:
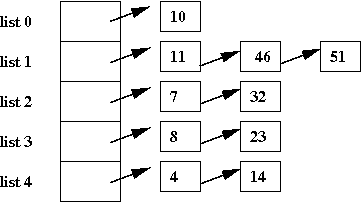
- In this case, most of the lists are small (size 1 or 2).
- If we wanted to search for '23', we'd go to list 3 and look
for it.
⇒
Since the list is smaller, the search time is less than a
full-list search.
- But: how do we know which list '23' is in?
In-Class Exercise 17:
For the above list, can you tell what the pattern is? What simple
calculation takes a number K and tells you which list K should belong to?
More details:
- The collection of lists is implemented as an array of lists.
⇒
Thus, list 3 is really the 4-th position in the array of lists.
- Given an element K, we want a function f(K) to tell
us which list it should belong to.
⇒
This is used in both insertion and search.
- Terminology: the function f() is called a hash function.
- Terminology: in the hashing jargon, a list is called a bucket.
- To insert an element K:
- Compute f(K).
- Insert K in list# f(K).
- To search for an element K:
- Compute f(K).
- Do a regular list-search in list# f(K).
- Typically, the number of linked lists is large:
- To store 1000 elements, we'd use at least 1000 lists.
⇒
1000 buckets.
- To store 108 elements, we'd probably use
something like 105 buckets.
- There's no fixed rule
⇒
For fast access, the more buckets the better.
Storing strings:
- Can we design a hash function for strings?
- Thus, we'd want a function f() such that
we could compute f("Ewok").
- What should be output of f() be?
⇒
f() should result in an integer between 0 and M-1, where
M is the number of lists.
- Let's try this:
f("Ewok") = sum of the ascii letters in the string
⇒
But what if that exceeds M?
- Solution:
f("Ewok") = (sum of ascii letters in the string) mod M
⇒
Any number mod M lies in the range 0,...,M-1.
- Real hash functions are similar.
- Java provides a hashCode() method in the class
String and in many other fundamental classes as well.
Let's look at pseudocode:
- Pseudocode for insertion:
Algorithm: set (key, value)
Input: key-value pair
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
// No list present, so create one
3. table[entry] = new linked list;
4. table[entry].set (key, value)
5. else
6. // Otherwise, add to existing list
7. table[entry].set (key, value)
8. endif
- Similarly, for search:
Algorithm: get (key)
Input: search-key
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
3. return null
4. else
5. return table[entry].search (key)
6. endif
Finally, our implementation in Java:
public class OurHashMap {
int numBuckets = 100; // Initial number of buckets.
OurLinkedListMap[] table; // The hashtable.
int numItems; // Keep track of number of items added.
// Constructor.
public OurHashMap (int numBuckets)
{
this.numBuckets = numBuckets;
table = new OurLinkedListMap [numBuckets];
numItems = 0;
}
public void set (KeyValuePair kvp)
{
if ( contains (kvp.key) ) {
return;
}
// Compute hashcode and therefore, which table entry (list).
int entry = Math.abs(kvp.key.hashCode()) % numBuckets;
// If there's no list there, make one.
if (table[entry] == null) {
table[entry] = new OurLinkedListMap ();
}
// Add to list.
table[entry].set (kvp);
numItems ++;
}
public boolean contains (String key)
{
// Compute table entry using hash function.
int entry = Math.abs(key.hashCode()) % numBuckets;
if (table[entry] == null) {
return false;
}
// Use the contains() method of the list.
return table[entry].contains (key);
}
public KeyValuePair get (String key)
{
// Similar to contains.
int entry = Math.abs(key.hashCode()) % numBuckets;
if (table[entry] == null) {
return null;
}
return table[entry].get (key);
}
}
In-Class Exercise 18:
Download OurHashMap.java
and HashMapExample.java.
Implement the method printBucketDistribution()
in OurHashMap so that it prints the size of each linked-list.
Then modify HashMapExample so that you try different numbers
of buckets. How many buckets are needed to ensure that each
list has at most one element?
Analysis:
- If each bucket has only a few elements
⇒
Fixed (smaller) number of items in each list.
⇒
O(1) time to search/insert in a list.
- Next, suppose we assume that the hash function itself takes
very little time (O(1)) to compute.
⇒
Then, it takes O(1) time to insert or search in a hashtable
⇒
Optimal!
- Thus, let's add hashing to our comparison so far:
| Data structure | Insertion | Search |
| LinkedList | O(1) | O(n) |
| ArrayList | O(n)? | O(n) |
| SortedList | O(n) | O(log(n)) |
BinaryTree
(balanced) | O(log(n)) | O(log(n)) |
| Hashtable | O(1) | O(1) |
Caveats:
- The performance depends on the lists being very small
⇒
This may not happen for very large number of elements
- For large data (large n) and M buckets, we can
expect n/M elements per list.
⇒
Search/insertion time will take at least n/M.
- We also need the hash function to spread the data uniformly
across the buckets
⇒
Need a good hash function, and some luck (with the data)
What we haven't covered in hashing:
- There are many varieties of hash tables.
- You can create hash-trees (trees of hashtables, with a
different hash function used at each node).
- One can build hash functions based on data to ensure uniform spread.
© 2006-2020, Rahul Simha & James Taylor (revised 2020)