Module 9: Recursion, Part II
Supplemental material
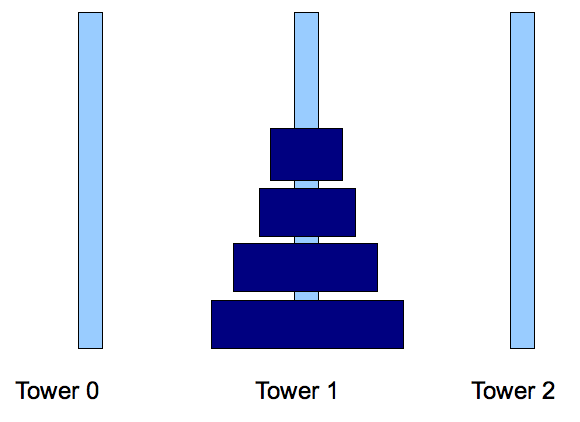
The Tower of Hanoi
In the Tower of Hanoi puzzle:
- There are three stacks (towers), numbered 0, 1, 2.
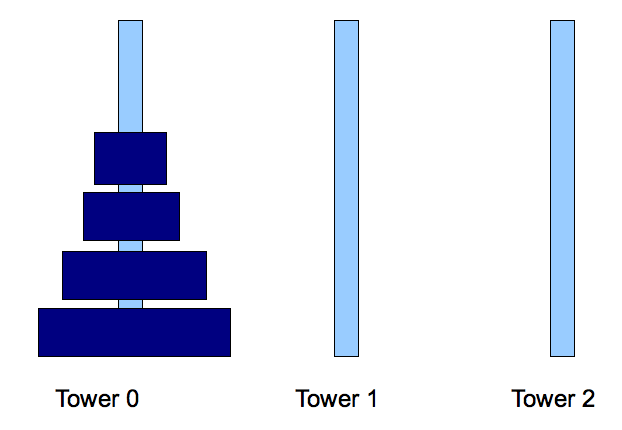
- There are N disks numbered 0, ..., N-1.
=>
0 is the smallest.
- Initially, the disks are placed in tower 0, in the
order largest to smallest.
=>
Smallest on top.
- Goal: to move the disks to tower 1 using only
legal moves.
- What's a legal move?
- You can move only a disk at the top of a tower.
- You can move only one disk at a time.
- You cannot place a disk on top of a smaller one.
We will solve the problem using (of course) recursion:
- There are three key steps in the recursion:
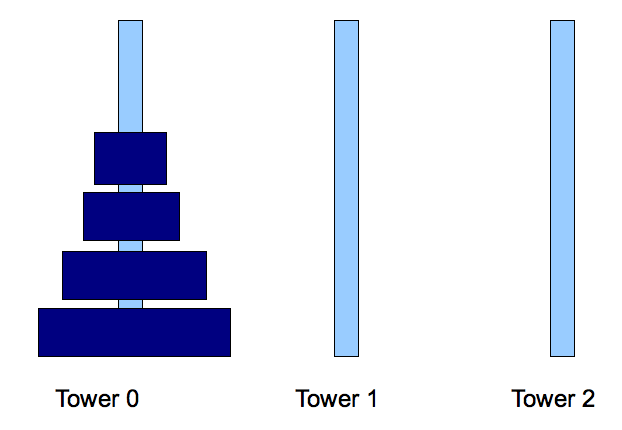
- Step 1: move disks 0, ..., N-2 from tower 0 to tower 2
=>
Sub problem of smaller size.
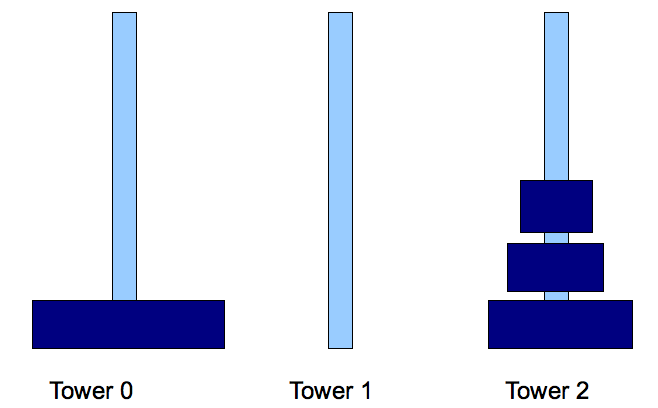
- Step 2: move disk N-1 from tower 0 to tower 1.
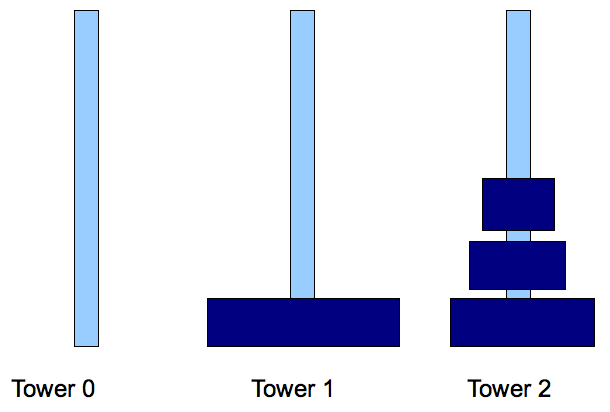
- Step 3: move disks 0, ..., N-2 from tower 2 to tower 1.
=>
Sub problem of smaller size.
- In pseudocode (without base case):
Algorithm towerOfHanoi (n, i, j)
Input: Disks numbered 0, ..., n are to be moved from tower i to tower j
1. // ... base case ...
// First find the third tower, other than i and j:
2. k = otherTower (i, j)
// Step 1: move disks 0,..,n-1 from i to k
3. towerOfHanoi (n-1, i, k)
// Step 2: move disk# n from i to j
4. move (n, i, j)
// Step 3: move disks 0,...,n-1 from k to j
5. towerOfHanoi (n-1, k, j)
- The base case: move a single disk
Here's the program:
(source file)
public class TowerOfHanoi {
public static void main (String[] argv)
{
// A 3-disk puzzle:
System.out.println ("3-Disk solution: ");
solveHanoi (2, 0, 1);
// A 4-disk puzzle:
System.out.println ("4-Disk solution: ");
solveHanoi (3, 0, 1);
}
static void solveHanoi (int n, int i, int j)
{
// Bottom-out.
if (n == 0) {
// The smallest disk.
move (0, i, j);
return;
}
int k = other (i, j);
solveHanoi (n-1, i, k); // Step 1.
move (n, i, j); // Step 2.
solveHanoi (n-1, k, j); // Step 3.
}
static void move (int n, int i, int j)
{
// For now, we'll merely print out the move.
System.out.println ("=> Move disk# " + n + " from tower " + i + " to tower " + j);
}
static int other (int i, int j)
{
// Given two towers, return the third.
if ( (i == 0) && (j == 1) ) {
return 2;
}
else if ( (i == 1) && (j == 0) ) {
return 2;
}
else if ( (i == 1) && (j == 2) ) {
return 0;
}
else if ( (i == 2) && (j == 1) ) {
return 0;
}
else if ( (i == 0) && (j == 2) ) {
return 1;
}
else if ( (i == 2) && (j == 0) ) {
return 1;
}
// We shouldn't reach here.
return -1;
}
}
Note:
- The above program merely prints out the moves needed
=>
We don't actually maintain the state of each tower.
Next, suppose we want to maintain the state of each tower:
- The ideal data structure is a stack.
- We'll use one stack for each tower.
Here's the program:
(source file)
import java.util.*;
public class TowerOfHanoi2 {
// towers[0], towers[1] and towers[2] are the three stacks.
static Stack<Integer>[] towers;
public static void main (String[] argv)
{
// A 3-disk puzzle:
System.out.println ("3-Disk solution: ");
solveHanoi (2, 0, 1);
// A 4-disk puzzle:
System.out.println ("4-Disk solution: ");
solveHanoi (3, 0, 1);
}
static void solveHanoi (int n, int i, int j)
{
// Create the three stacks.
towers = new Stack [3];
for (int k=0; k<3; k++) {
towers[k] = new Stack<Integer>();
}
// Put disks 0,...,n on stack 0.
for (int k=n; k>=0; k--) {
towers[0].add (k);
}
// Print the initial stack.
printTowers ();
// Now solve recursively. Note: this is the method below.
solveHanoiRecursive (n, i, j);
}
static void solveHanoiRecursive (int n, int i, int j)
{
// Bottom-out.
if (n == 0) {
move (0, i, j);
return;
}
int k = other (i, j);
solveHanoiRecursive (n-1, i, k); // Step 1.
move (n, i, j); // Step 2.
solveHanoiRecursive (n-1, k, j); // Step 3.
}
static void move (int n, int i, int j)
{
// Pull out the top disk on stack i.
int topVal = towers[i].pop();
// Put it on stack j.
towers[j].push (topVal);
// Print status.
System.out.println ("Towers after moving " + n + " from tower " + i + " to tower " + j);
printTowers ();
}
static int other (int i, int j)
{
// ...
}
static void printTowers ()
{
for (int i=0; i<towers.length; i++) {
System.out.print ("Tower " + i + ": ");
if ( ! towers[i].isEmpty() ) {
for (Integer I: towers[i]) {
System.out.print (" " + I);
}
}
System.out.println ();
}
}
}
Note:
- Since we needed to create the stacks ahead of time, we moved
the recursive part of the code into a new recursive method solveHanoiRecursive().
- To remove a disk from the top of a tower, we pop() from
that tower (stack):
// Pull out the top disk on stack i.
int topVal = towers[i].pop();
- To place a disk on top of a tower, we push() it:
// Put it on stack j.
towers[j].push (topVal);
- Notice how printTowers() uses the "collection"
version of the for-loop:
if ( ! towers[i].isEmpty() ) {
// New type of for-loop:
for (Integer I: towers[i]) {
System.out.print (" " + I);
}
}
- A strange compilation message:
- In compiling the above program (with a Java 1.5 compiler), we
get a warning (not an error):
Note: TowerOfHanoi2.java uses unchecked or unsafe operations.
Note: Recompile with -Xlint:unchecked for details.
- This allows you to continue with execution.
- You can, as it suggests, re-compile with the
-Xlint:unchecked option:
javac -Xlint:unchecked TowerOfHanoi2.java
- What you see as a result:
TowerOfHanoi2.java:25: warning: [unchecked] unchecked conversion
found : java.util.Stack[]
required: java.util.Stack[]
towers = new Stack [3];
^
- The compiler did not like the statement:
towers = new Stack [3];
- So, should this instead have been
towers = new Stack<Integer> [3];
as one might intuitively expect?
- Unfortunately, that results in a compilation error.
- The reason is quite esoteric and has to do with the
gory details of generic types are handled in Java.
- Essentially, it boils down to this: a declaration like
towers = new Stack<Integer> [3];
is unsafe because one can assign non-Integer stacks to
towers, which is why the compiler doesn't allow it.
- Thus, we are left with using the slightly less unsafe
towers = new Stack [3];
which the compiler allows but warns against.
- Generic types in Java constitute a large and somewhat
advanced topic, too complicated for this course.
An application: disk backup schedules
- Suppose we have four disks (A, B, C and D) on which we wish to
perform backups each day.
=>
This is a different meaning of disk (hard drive,
removable media)
- Each day we need to choose a disk on which to backup
=>
The backup schedule.
- One option is to go round-robin
Day 0 - use disk A
Day 1 - use disk B
Day 2 - use disk C
Day 3 - use disk D
Day 4 - use disk A
Day 5 - use disk B
...
(and so on)
- With this system, we can only go back at most four days.
- We are not able to retrieve the state of the system from,
say, 6 days ago.
- Another approach: stagger the disks:
Day 0 - use disk A
Day 1 - use disk B
Day 2 - use disk A
Day 3 - use disk C
Day 4 - use disk A
Day 5 - use disk B
Day 6 - use disk A
Day 7 - use disk D
Day 8 - use disk A
...
(and so on)
- With this approach, we'd have a distribution like
Disk A - 1 or 2 days before
Disk B - at most 4 days before
Disk C - at most 8 days before
Disk D - at most 16 days before
- This distribution allows a deeper reach into the past.
- The sequence above is exactly the Tower-of-Hanoi move
sequence for disks numbered A, B, C and D.
Recursion: a review
First, let's review a simple example from Module 4:
- Recall the recursive computation of power:
// Compute ab
static int power (int a, int b)
{
// Bottom-out:
if (b == 0) {
return 1;
}
// Recursion:
return (a * power (a, b-1));
}
- What's important:
- We must test for the bottom out case before recursing.
- The bottom-out case tests the value (or values) of the
parameter (or parameters) that changes in the recursion.
=>
These are the parameters that control the recursion.
- The recursive calls must change (usually decrease) the
parameters that control the recursion.
=>
Above, there is only one recursive call, but Tower of Hanoi has two.
- How recursion works:
- Each method call creates an activation record on
the system stack.
- The activation record consists of space allocated for the
particular parameters and local variables for that method call.
- Thus, a recursive call results in a new activation record
for each such recursive call.
=>
This is why each execution of the method retains its own
parameters and local variables.
- The activation record also knows that when execution of a
method call completes, execution returns to the calling method
just after the called-method was called.
- For recursion it's no different except that it's the same
code involved in all method calls.
- The best way to understand recursion initially is to draw
the stack picture and work through an example.
Let's now review another example from Module 4:
- This is the permutation seating example where we print the arrangement:
// The parameters to this method are:
// numSpaces - total number of remaining seats available
// numRemaining - total number of people left to seat
// seats - an array where seats[i]==0 if seat is available
// person - which person we need to seat
static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
{
// Bottom-out case.
if (numRemaining == 0) {
// Print.
System.out.println ( Arrays.toString(seats) );
return;
}
// Otherwise, non-base case: look for an empty spot for "person"
for (int i=0; i < seats.length; i++) {
if (seats[i] == 0) {
// Empty spot.
seats[i] = person;
// Recursively assign remaining, starting with person+1
printPermutations (numSpaces-1, numRemaining-1, seats, person+1);
// Important: we need to un-do the seating for other trials.
seats[i] = 0;
}
} //end-for
}
- What's similar about this recursive method:
- The parameter that controls recursion is: numSpaces
=>
This is what we check in the bottom-out case.
- Other parameters pass along information: person
and seats.
- What's different (from the power() example):
- When we fill in the seats array, we un-do
this assignment after the recursive call:
// Make some change to a parameter:
seats[i] = person;
// Recurse:
printPermutations (numSpaces-1, numRemaining-1, seats, person+1);
// Un-do the change (restore the original) for future recursions:
seats[i] = 0;
Two types of recursion:
- Recursion where you don't un-do changes.
=>
Sometimes this is called tail recursion.
- Recursion where you need to un-do changes so that you can
properly explore all possibilities
=>
Sometimes this is called recursion with backtracking.
- Many examples of tail-recursion can easily be written
non-recursively (using iteration)
=>
For many of these examples (power, factorial, fibonacci), it's
better to use iteration.
- However, when there's backtracking, it can be very difficult
to avoid recursion.
Maze construction and traversal: a (long) example of recursion with backtracking
We will now examine a maze application in detail to illustrate
recursion with backtracking:
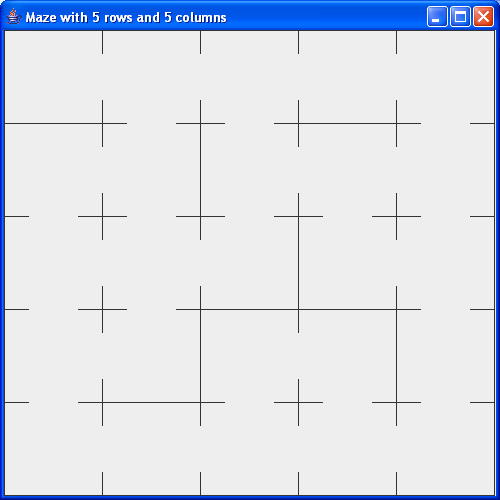
- First, we will use recursion to create a maze like this:
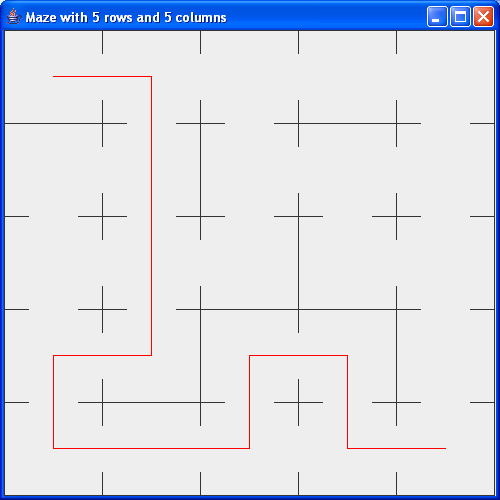
- Then, we will use recursion to solve such a maze (by
finding a path from a given start cell (e.g., the topleft) to a
given end cell (e.g., the bottom right):
- We will put a whole bunch of useful code in a class called
Maze and instead focus on using that class through
its methods.
- We'll use this cell-numbering convention:
- Rows start numbering at 0, and increase downwards.
- Columns start at 0 and increase rightwards.
Thus, the topleft cell is (0,0). The one to its right is (0,1) and
the one directly below is (1,0).
To start with, let's examine the methods in the class Maze:
- The constructor: we create an instance by specifying the number
of rows and columns:
Maze maze = new Maze (5, 5);
Our examples will use square mazes.
- display(): call this method to display the maze:
Maze maze = new Maze (5, 5);
// Bring up the GUI:
maze.display ();
- breakWall():
- Initially, the maze consists of complete cells. To actually
create a walkable maze, we will "break walls" between neighboring cells.
- For example, we can break the wall between cells (3,4) and
(2,4) as follows:
Maze maze = new Maze (5, 5);
// Note the use of the Coord class:
Coord c1 = new Coord (3,4);
Coord c2 = new Coord (2,4);
maze.breakWall (c1, c2);
maze.display ();
Or, alternatively, with shorter code:
Maze maze = new Maze (5, 5);
// Create an instance directly in the method argument list:
maze.breakWall (new Coord(3,4), new Coord (2,4));
maze.display ();
- The Coord class looks like this:
public class Coord {
public int row=-1, col=-1;
public Coord (int r, int c)
{
row = r;
col = c;
}
public String toString ()
{
return "[" + row + "," + col + "]";
}
}
- Thus, to access the stored coordinates:
Coord c = new Coord (3,4);
System.out.println ("Row=" + c.row + " Col=" + c.col);
// Or, to print both using toString():
System.out.println (c);
- A number of methods (in the class
Maze)
allow us to mark and un-mark cells as visited:
- markVisited (Coord c): mark cell c as visited.
- markUnVisited (Coord c): mark cell c as not
visited.
- markAllUnvisited(): mark all cells as unvisited.
- isVisited (Coord c): see whether cell c has
been visited.
- A number of methods related to fetching a list (array) of a
cell's neighbors:
- Coord[] getUnvisitedClosedNeighbors (Coord c): get
cell c's neighbors that are closed off from c
(there's a wall between) and haven't been visited yet.
- Coord[] getClosedNeighbors (Coord c): get neighbors
of c that share a wall (unbroken) with c whether
visited or not.
- Coord[] getUnvisitedOpenNeighbors (Coord c): get
those neighbors of c for which we can walk through to the
neighbor (no wall) and which haven't been visited.
Each of these methods return an array of Coord instances.
- A few additional useful methods:
- copy(): make a full copy of the maze, as in:
Maze m = new Maze (5,5);
// ... do stuff: break walls etc ...
Maze m2 = m.copy();
// Now m2 is a copy of m. Making changes to m won't affect m2.
- setSolutionPath (LinkedList<Coord>
solutionPath): we will call this method once we have
constructed a solution.
We'll now write our first attempt:
- We will try to generate a maze path of a given path length.
- The key idea:
Algorithm: recursiveGenerate (Coord c)
1. if path-length has been reached
2. return
// Otherwise ...
3. c' = Pick a random neighbor of cell c
4. recursiveGenerate (c')
Here's the program:
(source file)
public class MazeMaker {
// These variables will be used across methods:
static int desiredPathLength;
static Maze maze;
public static void main (String[] argv)
{
generateMaze (5, 5);
}
public static void generateMaze (int numRows, int numCols)
{
maze = new Maze (numRows, numCols);
// We want to generate a path of this length:
desiredPathLength = numRows * numCols;
// Initially, we'll start with the top left cell and mark that as visited.
Coord start = new Coord (0, 0);
maze.markVisited (start);
// Generate the maze path recursively.
boolean found = recursiveGenerate (start, 1);
if (! found) {
System.out.println ("Could not create the whole maze");
}
maze.display();
}
static boolean recursiveGenerate (Coord c, int pathLength)
{
// Bottom out condition 1:
if (pathLength == desiredPathLength) {
// Done. We've create a maze path of the desired length.
return true;
}
// Bottom out condition 2: see if there's a neighbor to visit.
Coord[] validNeighbors = maze.getUnvisitedClosedNeighbors (c);
if ((validNeighbors == null) || (validNeighbors.length == 0)) {
// There's no neighbor whose wall we can break. So quit trying.
return false;
}
// Otherwise, pick a random neighbor and proceed.
int i = UniformRandom.uniform (0, validNeighbors.length-1);
// Break the wall and mark the neighbor as visited.
maze.breakWall (c, validNeighbors[i]);
maze.markVisited (validNeighbors[i]);
// Recurse.
return recursiveGenerate (validNeighbors[i], pathLength+1);
}
}
Next attempt:
- Simple tail recursion can get stuck.
=>
We need a way to "un-do" paths and try different neighbors.
- We will pick a neighbor to explore recursively
=>
If that doesn't work out, we'll try another.
Here's the program:
(source file)
public class MazeMaker2 {
static int desiredPathLength;
static Maze maze;
public static void main (String[] argv)
{
generateMaze (5, 5);
}
public static void generateMaze (int numRows, int numCols)
{
maze = new Maze (numRows, numCols);
desiredPathLength = numRows * numCols;
// Initially, we'll start with the top left cell.
Coord start = new Coord (0, 0);
maze.markVisited (start);
// Generate the maze path recursively.
boolean found = recursiveGenerate (start, 1);
if (! found) {
System.out.println ("Could not create the whole maze");
}
maze.display();
}
static boolean recursiveGenerate (Coord c, int pathLength)
{
// Bottom out condition 1:
if (pathLength == desiredPathLength) {
return true;
}
// Bottom out condition 1: see if we're stuck.
Coord[] validNeighbors = maze.getUnvisitedClosedNeighbors (c);
if ((validNeighbors == null) || (validNeighbors.length == 0)) {
return false;
}
// Otherwise, we have some neighbors to explore.
// Permute the directions randomly.
permute (validNeighbors);
for (int i=0; i < validNeighbors.length; i++) {
// Try neighbor i.
maze.breakWall (c, validNeighbors[i]);
maze.markVisited (validNeighbors[i]);
boolean ok = recursiveGenerate (validNeighbors[i], pathLength+1);
if (ok) {
// If neighbor i worked out, great.
return true;
}
// Otherwise, undo assignment to i.
maze.fixWall (c, validNeighbors[i]);
maze.markUnvisited (validNeighbors[i]);
} // end-for
// Couldn't make it work.
return false;
}
static void permute (Coord[] coords)
{
for (int i=0; i < coords.length; i++) {
// Find a random element to place into i-th place.
int k = (int) UniformRandom.uniform (i, coords.length-1);
Coord temp = coords[i];
coords[i] = coords[k];
coords[k] = temp;
}
}
}
Note:
- The key idea is to try as many neighbors as needed:
Algorithm: recursiveGenerate (Coord c)
1. if path-length has been reached
2. return true
3. endif
// Otherwise ...
4. for each neighbor c' of c
5. found = recursiveGenerate (c')
6. if found
7. return true
8. endif
9. endfor
// We reach here only if every neighbor did not work out.
10. return false
- Note how we un-do a broken wall:
for (int i=0; i < validNeighbors.length; i++) {
// Try neighbor i.
maze.breakWall (c, validNeighbors[i]);
maze.markVisited (validNeighbors[i]);
// ... recursion here ...
// To un-do: repair the wall and mark as UNvisited.
maze.fixWall (c, validNeighbors[i]);
maze.markUnvisited (validNeighbors[i]);
} // end-for
A maze with choices:
- The above maze path has no choices
=>
There's only one way from the topleft to the end of the path.
- We will build upon this to create a maze with choices
=>
After generating the long path, we'll break some random walls.
Here's the program:
(source file)
public class MazeMaker3 {
// ... variables ...
public static void main (String[] argv)
{
generateMaze (5, 5);
}
public static void generateMaze (int numRows, int numCols)
{
// ... create and generate single-path maze ...
// Break a few more walls, randomly.
breakRandomWalls (maze, 10);
maze.display();
}
static boolean recursiveGenerate (Coord c, int pathLength)
{
// ... same as before ...
}
static void breakRandomWalls (Maze maze, int numWalls)
{
for (int k=0; k < numWalls; k++) {
// Create random coordinates, i.e., identify a random cell.
int x = UniformRandom.uniform (0, maze.numRows-1);
int y = UniformRandom.uniform (0, maze.numCols-1);
Coord c = new Coord (x,y);
// Get its neighbors that are separated by a wall.
Coord[] validNeighbors = maze.getClosedNeighbors (c);
if (validNeighbors != null) {
// Pick one and break the wall.
int m = UniformRandom.uniform (0, validNeighbors.length-1);
maze.breakWall (c, validNeighbors[m]);
}
}
}
}
Let's turn our attention to solving the maze:
- We'll first try a simple idea:
Algorithm: recursivelyFindPath (Coord c)
1. if c is the end
2. return true
3. endif
4. // Otherwise search further ...
5. c' = pick a random "open" neighbor
6. if c' is null
// Stuck: couldn't find a path.
7. return false
8. endif
9. return recursivelyFindPath (c')
Here's the program:
(source file)
import java.util.*;
public class MazeMaker4 {
static int desiredPathLength;
static Maze maze;
public static void main (String[] argv)
{
Maze maze = generateMaze (5, 5);
if (maze != null) {
// We will seek a path from the top-left to the bottom-right corner.
Coord start = new Coord (0,0);
Coord end = new Coord (4,4);
solveMaze (maze, start, end);
maze.display ();
}
else {
System.out.println ("Maze creation did not work");
}
}
// A path is a list of cells, i.e., a list of Coord instances.
static LinkedList<Coord> solutionPath;
static void solveMaze (Maze maze, Coord start, Coord end)
{
// We'll mark visited cells as we go along our path. Initially:
maze.markAllUnvisited ();
// Mark the start cell as visited.
maze.markVisited (start);
// Create the list.
solutionPath = new LinkedList<Coord> ();
// Recursively find the path and fill in coord's into the list.
recursivelyFindPath (maze, start, end);
// Pass the path into the GUI.
maze.setSolutionPath (solutionPath);
}
static boolean recursivelyFindPath (Maze maze, Coord c, Coord end)
{
// First add the current cell into the path.
solutionPath.add (c);
// If we've reached the end, we're done.
if ( (c.row == end.row) && (c.col == end.col) ) {
return true;
}
// Otherwise, let's find a neighbor to explore.
Coord[] validNeighbors = maze.getUnvisitedOpenNeighbors (c);
if (validNeighbors == null) {
// If there aren't any, we're done, but couldn't find a path.
return false;
}
// Take the first one and explore from there.
maze.markVisited (validNeighbors[0]);
return recursivelyFindPath (maze, validNeighbors[0], end);
}
// ... Maze generation code ... same as before ...
}
A solution that works:
- When exploring a neighbor, we need a way to un-do (backtrack)
if it doesn't lead to a solution.
- The idea is to try all possible neighbors, as many as needed:
Algorithm: recursivelyFindPath (Coord c)
1. if c is the end
2. return true
3. endif
4. // Otherwise search further ...
5. for each "open" neighbor c'
6. found = recursivelyFindPath (c')
7. if found
8. add c' to path
9. return true
10. endif
10. endfor
11. return false
Here's the program:
(source file)
import java.util.*;
public class MazeMaker5 {
// ... variables ... same as before (for generation) ...
public static void main (String[] argv)
{
// ... same ...
}
// A path is a list of cells, i.e., a list of Coord instances.
static LinkedList<Coord> solutionPath;
static void solveMaze (Maze maze, Coord start, Coord end)
{
// We'll mark visited cells as we go along our path. Initially:
maze.markAllUnvisited ();
// Mark the start cell as visited.
maze.markVisited (start);
// Create the list.
solutionPath = new LinkedList<Coord> ();
// Recursively find the path and fill in coord's into the list.
recursivelyFindPath (maze, start, end);
// The start node gets added last. Why?
solutionPath.addFirst (start);
// Pass the path into the GUI.
maze.setSolutionPath (solutionPath);
}
static boolean recursivelyFindPath (Maze maze, Coord c, Coord end)
{
// If we've reached the end, we're done.
if ( (c.row == end.row) && (c.col == end.col) ) {
return true;
}
// Otherwise, let's find a neighbor to explore.
Coord[] validNeighbors = maze.getUnvisitedOpenNeighbors (c);
if (validNeighbors == null) {
// If we couldn't find any neighbors to explore, we're stuck.
return false;
}
// Try each neighbor, as many as needed.
for (int i=0; i < validNeighbors.length; i++) {
// Try neighbor i.
maze.markVisited (validNeighbors[i]);
boolean found = recursivelyFindPath (maze, validNeighbors[i], end);
if (found) {
// Notice that we add this to the front of the list, and only
// after the solution has been found up to here.
solutionPath.addFirst (validNeighbors[i]);
return true;
}
// If neighbor i didn't work out, un-do the visit and continue.
maze.markUnvisited (validNeighbors[i]);
}
// If we reached here, then none of the neighbors worked out.
return false;
}
}
The N-Queens problem
In this problem:
- We are given an N x N chessboard and M queens
(where M <= N).
- The goal is to place the queens on the board so that no
queen "attacks" another.
- For example (N=8):
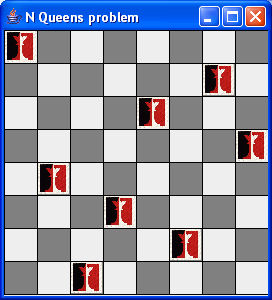
- Recall that a queen can attack any square in its row, column
or diagonal, e.g.
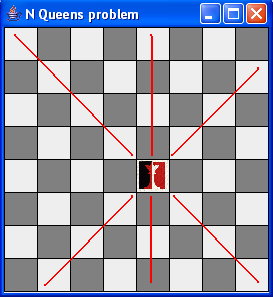
We will of course solve this recursively:
- This is another example of recursion with backtracking.
- Key ideas:
- We'll proceed columm-by-column (left to right).
- When solving for the current column, try to place
a queen on each possible row, and solve the sub-problem
(starting with the next column) recursively.
- Pseudocode:
Algorithm: solve (n, c)
Input: n = the number of queens to assign, c = the column to start with
// ... Bottom-out conditions ... (we'll do this later)
1. for each row r
2. if [r,c] is a non-attacked square
3. place queen n on cell [r,c]
4. found = solve (n-1, c+1) // Assign remaining n-1 recursively
5. if (found)
6. return true
7. endif
8. endif
9. endfor
// We reach here if none of the rows in column c worked out.
10. return false
- Thus, we try every row for a queen and try to solve the
sub-problem with fewer queens.
=>
If if that gets solved, we can place the queen there and recurse back up
- The bottom-out conditions:
- Check if there are no more queens to assign
=>
Problem gets solved.
- Check if there are no more columns to try
=>
No solution exists.
- We will build a class called ChessBoard with
methods that hide most of the messy board-manipulation details:
- addQueen (row,col): add a queen in square [row,col].
- removeQueen (row,col): remove the queen in square [row,col].
- boolean isForbidden (row,col): see if [row,col] is an attacked square.
- display(): to bring up a GUI with the board displayed.
Here's the program:
(source file)
import java.awt.*;
import java.util.*;
public class NQueens {
static ChessBoard board;
public static void main (String[] argv)
{
solveQueens (8, 8);
}
static void solveQueens (int numQueens, int size)
{
board = new ChessBoard (size);
boolean solutionExists = solve (numQueens, 0);
if (! solutionExists) {
System.out.println ("No solution for " + numQueens + " on a " + size + " x " + size + " board");
return;
}
System.out.println ("Solution found for " + numQueens + " on a " + size + " x " + size + " board");
System.out.println (board);
board.display();
}
static boolean solve (int numQueens, int whichCol)
{
// Bottom-out condition 1:
if (numQueens == 0) {
// None to assign - done.
return true;
}
// Bottom-out condition 2:
if (whichCol >= board.size()) {
// No columns left to try - done.
return false;
}
// Try every un-forbidden spot in each row.
for (int row=0; row < board.size(); row++) {
if ( ! board.isForbidden(row,whichCol) ) {
// Try this location.
board.addQueen (row, whichCol);
boolean solutionExists = solve (numQueens-1, whichCol+1);
if (solutionExists) {
return true;
}
// Else, un-do
board.removeQueen (row, whichCol);
}
}
// Couldn't find a solution.
return false;
}
}








