Module 8: Stacks, Queues, ADT's

Stacks: a simple example

What is a stack?

You always add items to the front (top)

You always remove items from the front (top)
=> you remove the most recently inserted item.

Here's a simple example we saw earlier in the Introduction:

import java.util.*;

public class StackExample {

    public static void main (String[] argv)
    {
	// Use java.util.Stack, and specialize it to String's.
        Stack<String> toDoList = new Stack<String> ();

        // Add some strings.
        toDoList.push ("Pay bills");
        toDoList.push ("Clean room");
        toDoList.push ("Do homework");
        toDoList.push ("See movie");
        toDoList.push ("Hang out");
        
        // Print.
        System.out.println ("My priorities: ");
        while (! toDoList.isEmpty() ) {
            String nextPriority = toDoList.pop ();
            System.out.println (" " + nextPriority);
        }
    }
    
}

Note:

The output is, as you might expect:

My priorities: 
 Hang out
 See movie
 Do homework
 Clean room
 Pay bills

The operations we've used are:
- push: place an item on top of the stack.
- pop: remove the item currently on top of the stack.
- isEmpty: test if the stack is empty.
They correspond to the Stack methods push(), pop() and isEmpty() (obviously).

Although we have created a stack of strings, we could just as easily create and use a stack of integers or various kinds of objects.

For example, here's an example that pushes a couple of integer's and prints them out in reverse order: (source file)

import java.util.*;

public class StackExample2 {

    public static void main (String[] argv)
    {
        Stack<Integer> numberStack = new Stack<Integer> ();

        // Push some numbers
	numberStack.push (1);
	numberStack.push (2);
	numberStack.push (3);
        
        // Print in reverse order by popping off the stack.
        while (! numberStack.isEmpty() ) {
            System.out.println (numberStack.pop());
        }
    }
    
}

A stack application: balancing parentheses

We'll use a stack to check whether the parentheses in a string of parentheses are matched:

The input will consist of a String containing only parentheses:

Example: "(()())" (Balanced).
Example: "(()(" (Unbalanced).

Each time we see ( (left paren) we will push it on the stack.

Thus, the stack is a list of "expectations" of corresponding right parens.

Each time we see a ) (right paren), we should expect its match on top of the stack.

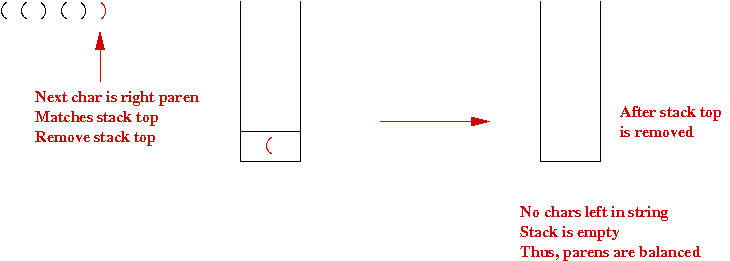
Consider this string of parentheses: "(()())"

Initially, the stack is empty
After scanning the first character in the string:
The next char is another left paren:
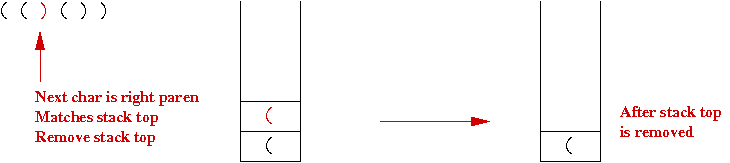
The next char is a right paren that matches the second char:
The next char is a left paren:
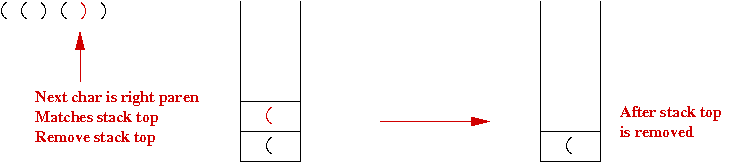
The fifth char is a right paren that matches the fourth char:
Finally, the last char is a right paren that matches the first char:

Here's the program: (source file)

import java.util.*;

public class ParenBalancing {

    public static void main (String[] argv)
    {
	// Test 1.
	String s = "()(())()";
	checkParens (s);

	// Test 2.
	s = "((())";
	checkParens (s);

	// Test 3.
	s = ")(";
	checkParens (s);
    }

    static void checkParens (String inputStr)
    {
	// Extract letters from String.
	char[] letters = inputStr.toCharArray();

	// We'll need a Character stack.
	Stack<Character> stack = new Stack<Character> ();

	boolean unbalanced = false;

	for (int i=0; i<letters.length; i++) {

	    if (letters[i] == '(') {
		// Push left paren.
		stack.push (letters[i]);
	    }
	    else if (letters[i] == ')') {
		// Right paren: we should have a match on the stack.
		char ch = stack.pop ();
		if (ch != '(') {
		    // Not a match.
		    unbalanced = true;
		    break;
		}
	    }

	} //end-for
	
	if ( (unbalanced) || (! stack.isEmpty()) ) {
	    System.out.println ("String " + inputStr + " has unbalanced parens");
	}
	else {
	    System.out.println ("String " + inputStr + " has balanced parens");	
	}

    }

}

Next, let's modify the above example to balance two types of parentheses simultaneously:

We'll assume the string contain only parentheses.
Example: "([()])" (Balanced).
Example: "((()]]" (Unbalanced).

Here's the program: (source file)

import java.util.*;

public class ParenBalancing3 {

    public static void main (String[] argv)
    {
	// Test 1.
	String s = "([()])";
	checkParens (s);

	// Test 2.
	s = "[][()]()";
	checkParens (s);

	// Test 3.
	s = "((())]";
	checkParens (s);

	// Test 4.
	s = "[)(]";
	checkParens (s);
    }


    static void checkParens (String inputStr)
    {
	char[] letters = inputStr.toCharArray();
	Stack<Character> stack = new Stack<Character> ();

	boolean unbalanced = false;

	for (int i=0; i<letters.length; i++) {

	    if ( (letters[i] == '(') || (letters[i] == '[') ) {
		// Push every left paren of each kind.
		stack.push (letters[i]);
	    }
	    else if (letters[i] == ')') {
		// We should have a '(' match on the stack
		char ch = ')';
		if (! stack.isEmpty() ) {
		    ch = stack.pop ();
		}
		if (ch != '(') {
		    // Not matched => unbalanced.
		    unbalanced = true;
		    break;
		}
	    }
	    else if (letters[i] == ']') {
		// We should have a '[' match on the stack
		char ch = ']';
		if (! stack.isEmpty() ) {
		    ch = stack.pop ();
		}
		if (ch != '[') {
		    // Not matched.
		    unbalanced = true;
		    break;
		}
	    }

	} // end-for
	
	if ( (unbalanced) || (! stack.isEmpty()) ) {
	    System.out.println ("String " + inputStr + " has unbalanced parens");
	}
	else {
	    System.out.println ("String " + inputStr + " has balanced parens");	
	}
    }

}

Another stack application: palindromes

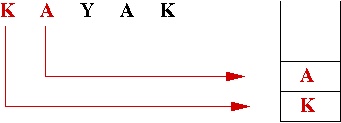
Yet another way to check if a string is a palindrome:

Example: consider the string "kayak"

First phase: push the letters from the first half:

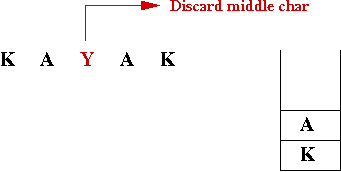
Remove the middle character if word is of odd length:

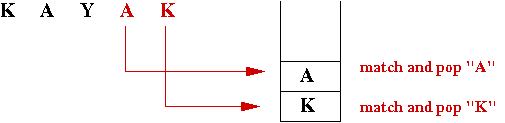
Second phase: match latter half:

Let's examine the program: (source file)

import java.util.*;

public class Palindrome {

    public static void main (String[] argv)
    {
	// Test 1.
        String str = "redder";
        System.out.println ( str + " " + checkPalindrome(str) );

	// Test 2.
        str = "river";
        System.out.println ( str + " " + checkPalindrome(str) );

	// Test 3.
        str = "neveroddoreven";
        System.out.println ( str + " " + checkPalindrome(str) );
    }
    

    static String checkPalindrome (String str)
    {
	// Extract the letters.
	char[] letters = str.toCharArray ();

	// Create an empty stack.
	Stack<Character> stack = new Stack<Character>();

	// The letters must "balance" up to the middle.
	int mid = letters.length / 2;

	// Push the first half.
	for (int i=0; i<mid; i++) {
	    stack.push (letters[i]);
	}

	// Odd or even? We have to adjust the mid-point accordingly.
	if (letters.length % 2 > 0) {
	    // Odd number => swallow middle letter.
	    mid = mid+1;
	}

	// Now check the second half.
	for (int i=mid; i<letters.length; i++) {
	    char ch = stack.pop ();
	    if (ch != letters[i]) {
		// Mismatch => not a palindrome.
		return "is not a palindrome";
	    }
	}

	return "is a palindrome";
    }

}

Note:

For a string of even length, the two characters at the middle have to be checked against each other
=> the two d's in redder
For a string of odd length, we need to ignore the middle letter
=> Ignore the v in civic

Building our own stack

Let's build our own stack data structure:

We'll do this for char's
=> Use it for the paren-balancing application.

We'll use a simple array to hold the stack.

Sample code:

public class OurStack {

    char[] letters;         // Store the chars in here.
    int top;                // letters[top]: next available space.


    // Constructor.

    public OurStack ()
    {
	letters = new char [100];
	top = 0;
    }



    public void push (char ch)
    {
        // Note: what if top >= letters.length?
	letters[top] = ch;
	top ++;
    }


    public char pop ()
    {
        // Note: what if top < 0?
        top --;
        return letters[top];
    }


    public boolean isEmpty ()
    {
	if (top == 0) {
	    return true;
	}
	else {
	    return false;
	}
    }

}

Let's improve this stack with some error checking: (source file)

public class OurStack {

    char[] letters;         // Store the chars in here.
    int top;                // letters[top]: next available space.


    // Constructor.

    public OurStack ()
    {
	letters = new char [100];
	top = 0;
    }


    public void push (char ch)
    {
        // Test for full stack.
        if (top >= letters.length) {
            System.out.println ("ERROR: OurStack.push(): stack overflow");
            return;
        }
        
	letters[top] = ch;
	top ++;
    }


    public char pop ()
    {
        // Test for empty stack.
	if (top <= 0) {
            System.out.println ("ERROR in OurStack.pop(): stack empty");
            // Still need to have a return statement, so we return some "junk letter".
            return '@';
	}

        top --;
        return letters[top];
    }


    public boolean isEmpty ()
    {
	if (top == 0) {
	    return true;
	}
	else {
	    return false;
	}
    }

}

Note:

The error recovery from pop() is a little artificial
=> We are still forced to return something.
In the Supplement, we describe how to use exceptions as a better way to handle errors.

The stack above can be used in our paren-balancing application: (source file)

import java.util.*;

public class OurStackExample {

    public static void main (String[] argv)
    {
	String s = "((()))";
	checkParens (s);

	s = "((())";
	checkParens (s);
    }

    static void checkParens (String inputStr)
    {
	char[] letters = inputStr.toCharArray();
	OurStack stack = new OurStack ();

        // ... code similar to earlier examples ...

    }

}

Next, let's use a linked-list instead of an array: (source file)

import java.util.*;

public class OurStack3 {

    // Use a linked list instead of an array.
    LinkedList<Character> list;


    public OurStack3 ()
    {
	// Can be unlimited in size now.
	list = new LinkedList<Character>();
    }


    public void push (char ch)
    {
        // No need to check for upper limit.
	list.add (ch);
    }


    public char pop ()
    {
	if (! list.isEmpty()) {
	    return list.removeLast();
	}
	else {
	    System.out.println ("ERROR in OurStack.pop(): stack empty");
	    return '@';
	}
    }


    public boolean isEmpty ()
    {
	return list.isEmpty();
    }

}

Note:

The code is a little cleaner:
- We don't have to keep track of the "top" since the list size is exactly the stack size.
- We can exploit list methods such as isEmpty().
The stack grows only as much as necessary.

ADT's

What's an ADT?

ADT = Abstract Data Type

There are many senses in which this term is used
=> We'll examine these below.

First meaning of ADT: a "standard" data structure with "well-known" operations:

Example: stack with operations push, pop, isEmpty.
Example: list with operations add, search, get(i).
What's important here are the meanings of the operations.
It's clear that the list operations are different from the stack operations.

Second meaning of ADT: the idea that implementations are hidden

We can implement a stack using an array, a list or use some other internal workings.
The internal workings shouldn't change the behavior of the operations as seen by users of the operations.
The internal workings could be changed without affecting the use of the ADT by others.
- Suppose our main() method uses a stack.
- Suppose the stack is really implemented with an array.
- If we changed the stack code so that it uses a linked-list, then we shouldn't have to change any code in main.

Third meaning of ADT: language features that support ADT's

Language feature: separate implementations in separate classes (and files).
Language feature: Use interface's in Java.

Let's look at an example of using interfaces.

First, we'll re-write our balanced-parens example as: (source file)

public class ParenBalancing5 {

    public static void main (String[] argv)
    {
	String s = "()(())()";

        // Use this stack implementation for the first example.
        StackImpl1 stack1 = new StackImpl1 ();
	ParenCheckTool.check (s, stack1);

	s = "((())";

        // Use another stack implementation for the second example.
        StackImpl2 stack2 = new StackImpl2 ();
	ParenCheckTool.check (s, stack2);
    }

}

Note:

We've put the real checking code in another class
=> We call the method check() in that class.
We also create a stack and pass that on to check().

So, what's in the class ParenCheckTool? (source file)

public class ParenCheckTool {

    // NOTE: checkParens() is written to accept an interface instead
    // of an actual class.

    static void check (String inputStr, OurStackInterface stack)
    {
        // This code below is complete unchanged from before ...

	char[] letters = inputStr.toCharArray();

	boolean unbalanced = false;
	for (int i=0; i < letters.length; i++) {
	    if (letters[i] == '(') {
		stack.push (letters[i]);
	    }
	    else if (letters[i] == ')') {
		// We should have a match on the stack.
		char ch = ')';
		if (! stack.isEmpty() ) {
		    ch = stack.pop ();
		}
		if (ch != '(') {
		    // Mismatch => unbalanced.
		    unbalanced = true;
		    break;
		}
	    }
	}
	
	if ( (unbalanced) || (! stack.isEmpty()) ) {
	    System.out.println ("String " + inputStr + " has unbalanced parens");
	}
	else {
	    System.out.println ("String " + inputStr + " has balanced parens");	
        }
    }

}

Next, examine the file OurStackInterface.java: (source file)

public interface OurStackInterface {

    // Signature, and only the signature, of the push() method:
    public void push (char ch);

    // Same for the pop() method:
    public char pop ();

    // Same for the isEmpty() method:
    public boolean isEmpty ();

}

Note:

An interface has only method signatures, no code.
An interface is really a specification.
Whichever class implements the interface must have bodies for the methods in the interface.

Next, let's look at the first implementation: (source file)

public class StackImpl1 implements OurStackInterface {

    // An array implementation ...
    char[] letters;         // Store the chars in here.
    int top;                // letters[top]: next available space.

    // ... the rest of the code is the same as in OurStack.java ...

}

Similarly, here's the second one: (source file)

import java.util.*;

public class StackImpl2 implements OurStackInterface {

    // Use a linked list instead of an array.
    LinkedList<Character> list;

    // ... rest of the code is the same as OurStack3.java ...

}

What's important to note:

Suppose the class ParenCheckTool is compiled.

Years later, we could change the code in the implementations and in ParenBalancing5:

public class ParenBalancing5 {

    public static void main (String[] argv)
    {
	String s = "()(())()";

        // Use this stack implementation for the first example.
        StackImpl3 stack3 = new StackImpl3 ();
	ParenCheckTool.check (s, stack3);

	s = "((())";

        // Use another stack implementation for the second example.
        StackImpl2 stack2 = new StackImpl2 ();
	ParenCheckTool.check (s, stack2);
    }

}

We would not have to re-compile ParenCheckTool
=> This is a key feature of Object-Oriented Programming (OOP).

Queues

What is a queue?

A queue is a list.

When you add something to the queue, you add it to the end of the list.

When you remove something from the queue, you remove it from the front of the list.

The most basic Queue ADT has three operations:

add: add an element to the end of the list.
remove: remove an element from the front of the list.
isEmpty: see if the queue is empty.

A more powerful queue might also implement methods like:

get(i): get the i-th element in the queue.
size: how many elements are in the queue?

Consider this example of a queue that uses Java's LinkedList to serve as our queue data structure: (source file)

import java.util.*;

public class QueueExample {

    public static void main (String[] argv)
    {
        // We'll use Java's LinkedList as our queue.
        LinkedList<String> taskQueue = new LinkedList<String>();

        // Add some strings.
        taskQueue.add ("Pay bills");
        taskQueue.add ("Clean room");
        taskQueue.add ("Do homework");
        taskQueue.add ("See movie");
        taskQueue.add ("Hang out");
        
        // Now extract in "queue" order using the removeFirst() method in LinkedList.
        System.out.println (taskQueue.removeFirst());
        System.out.println (taskQueue.removeFirst());
        System.out.println (taskQueue.removeFirst());
        System.out.println (taskQueue.removeFirst());
        System.out.println (taskQueue.removeFirst());

        System.out.println ("=> Tasks remaining: " + taskQueue.size());
    }

}

Note:

Because Java's LinkedList is used for other purposes (as a linked list!), it has a few variations of "remove" methods.
The method removeFirst() is what we need for the queue's remove operation.

Queue example: a strange card game

Consider the following two-person card game:

There are N cards numbered 0, ..., N-1.

Each player is dealt M cards from a shuffled deck.

Each player is required to keep their pile of cards face down
=> Players can't see the cards they haven't played yet.

There is a common pile, initially empty, onto which players will add their cards.

At every turn, each player "plays" by taking the card on top of their own pile and placing that in the common pile.

The cards are revealed when "played" on to the common pile.

If, in one turn, any one player's card exceeds the other's card by by more than 2, then that player gets to keep all the cards in the common pile.

For example, if player 2 plays "7" and player 1 plays "3", then player 2 scoops up the common pile and adds it to the bottom of their own pile.

The first player to have no cards remaining loses.

We will write a program to simulate the card game:

We'll use a queue for each player's pile.
We'll use a queue for the common pile.

Here's the program: (source file)

// This card game is a variation of the War card game described
// in the book "Object-Oriented Data Structures Using Java" by
// N.Dale, D.T.Joyce and C.Weems.

import java.util.*;

public class StrangeCardGame {

    public static void main (String[] argv)
    {
        // Use cards numbered 0,..,9 and deal 5 cards to each player.
	playGame (5, 10);
    }


    static void playGame (int dealSize, int numCards)
    {
        // Cards dealt out to player 1:
	LinkedList<Integer> player1 = new LinkedList<Integer>();
        // Cards dealt out to player 2:
	LinkedList<Integer> player2 = new LinkedList<Integer>();

        // The pile between the two players:
	LinkedList<Integer> pile = new LinkedList<Integer>();


        // Make the cards and shuffle them randomly.
	int[] cards = new int [numCards];
	for (int i=0; i<cards.length; i++) {
	    cards[i] = i;
	}
	shuffle (cards);

	// Deal cards to each player.
	int cardCount = 0;
	for (int k=0; k<dealSize; k++) {
	    player1.add (cards[cardCount]);
	    player2.add (cards[cardCount+1]);
	    cardCount += 2;                         	    // Note: += operator.
	}

	// Now play.
	boolean done = false;
	int round = 0;

	while (! done) {

	    // Each player plays their first card.
	    int player1first = player1.removeFirst ();
	    pile.add (player1first);
	    int player2first = player2.removeFirst ();
	    pile.add (player2first);

	    System.out.println ("Round 0: player1's card=" + player1first + "  player2's card=" + player2first);

	    if (player1first > player2first+2) {
		// Add pile into player 1's cards.
		addListToList (pile, player1);
		System.out.println ("  => player1 gets pile");
	    }
	    else if (player2first > player1first+2) {
		// Add pile into player 2's cards.
		addListToList (pile, player2);
		System.out.println ("  => player2 gets pile");
	    }
	    else {
		System.out.println ("  => both cards added to pile");
	    }

	    if (player1.isEmpty()) {
		System.out.println ("Player 2 wins!");
		done = true;
	    }
	    else if (player2.isEmpty()) {
		System.out.println ("Player 1 wins!");
		done = true;
	    }

	} //end-while

    }


    static void shuffle (int[] A)
    {
       // ... random permutation ...
    }


    static void addListToList (LinkedList<Integer> list1, LinkedList<Integer> list2)
    {
        // ... Extract every item in list1 and add them to list2 ...
    }

}

Note:

The queue's above are queues of Integer's.
There are three queues: one each for the two players, and one for the common pile.
The queue operations used are: add(), removeFirst() and isEmpty().

A GUI application

Consider the following simple animation:

We'll build a simple "game" in which an anteater will chase down ants to eat.

We'll put up a blank canvas on which a user can click to create ants.
=> These ants will go into a queue.

An anteater will systematically hunt down ants one by one
=> The next ant is taken from the head of the queue.

Only the anteater gets to move (to make things simple).

Here's the program (source file)

// Various import's needed for GUI's.
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
import javax.swing.event.*;
import java.util.*;            // This we need for LinkedList.


class AntEaterPanel extends JPanel {

    // We'll put all the ant-clicks into a queue, from which the anteater 
    // will pull out the next target.
    LinkedList<Point> antQueue = new LinkedList<Point>();

    Point antEater;    // The current position of the anteater.
    Point nextAnt;     // The position of the current ant being chased.


    // Constructor.

    public AntEaterPanel () 
    {
        // Listen to mouseclicks.
        this.addMouseListener (
            new MouseAdapter () {
                public void mouseClicked (MouseEvent e) 
                {
                    handleClick (e.getX(), e.getY());
                }
            }
                                    
        );
        
        // The anteater will run in a separate thread.
        Thread t = new Thread () {
                public void run () 
                {
                    move ();
                }
            };
        t.start ();
    }



    public void paintComponent (Graphics g)
    {
        super.paintComponent (g);

        // Clear drawing area.
        g.setColor (Color.white);
        Dimension D = this.getSize();
        g.fillRect (0,0, D.width, D.height);

        // Draw the ants.
        g.setColor (Color.gray);
        if (nextAnt != null) {
            g.fillOval (nextAnt.x-2,nextAnt.y-2, 4, 4);
        }
        for (Iterator<Point> iter=antQueue.iterator(); iter.hasNext(); ) {
            Point p = iter.next();
            g.fillOval (p.x-2,p.y-2, 4, 4);
        }

        // AntEater.
        g.setColor (Color.red);
        g.fillOval (antEater.x-10,antEater.y-10, 20, 20);
    }
    
    
    void draw ()
    {
        // Place a call to paintComponent(). 
        this.repaint ();
    }


    void handleClick (int x, int y)
    {
        // Add a new ant to the queue.
        antQueue.add (new Point(x,y));
        draw ();
    }
    

    void move ()
    {
        // This is where we'll start the anteater.
        antEater = new Point (0,0);
        
        while (true) {

            // Anteater sleeps 100 milliseconds.
            try {
                Thread.sleep (100);
            }
            catch (InterruptedException e) {
            }

            if (nextAnt == null) {
                if (! antQueue.isEmpty() ) {
                    // See if there's an ant to chase.                    
                    nextAnt = antQueue.removeFirst();
                }
            }
            else {
                if ( distance(nextAnt, antEater) < 10 ) {
                    // Eat the ant.
                    nextAnt = null;
                }
                else {
                    // Otherwise, step towards ant.
                    double theta = Math.atan2 ((nextAnt.y - antEater.y), (nextAnt.x - antEater.x));
                    double stepsize = 10.0;
                    antEater.x = (int) (antEater.x + stepsize*Math.cos(theta));
                    antEater.y = (int) (antEater.y + stepsize*Math.sin(theta));
                    draw ();
                }
            }
        }
    }


    double distance (Point p, Point q)
    {
        double distSq = (p.x-q.x)*(p.x-q.x) + (p.y-q.y)*(p.y-q.y);
        return Math.sqrt (distSq);
    }

} //end-panel



class AntEaterFrame extends JFrame {
    
    public AntEaterFrame ()
    {
        this.setTitle ("AntEater");
        this.setSize (300, 300);

        // The frame only consists of the panel.
        AntEaterPanel panel = new AntEaterPanel ();
        this.getContentPane().add (panel);

        this.setVisible (true);
    }

} //end-frame



public class AntEater {

    public static void main (String[] argv)
    {
        AntEaterFrame f = new AntEaterFrame ();
    }

}

Note:

Let's point out a few things from the GUI code:
- There are three parts to it: main(), the frame (AntEaterFrame) and the drawing area (AntEaterPanel).
- main() is very simple: we merely create an instance of the frame.
- The frame too is quite simple: we set the size, place an instance of the panel inside and make it visible.
- All the work is done inside the panel.
- To draw on the panel, we need to extend Java's JPanel class to override the paintComponent() method.
  => This is what is called for drawing to occur.
  => It's where we put our drawing code.
- The panel also listens for mouseclicks, which are placed in the queue.
- The panel also has the "logic" (anteater movement).
Let's focus on the use of a queue:
- Each click creates a new ant, which is placed in the queue (the add() operation).
- Once the anteater eats an ant, we look at the queue for the next ant (the removeFirst() operation).
- We also need to test whether the queue is empty.