TRANSFORMS in LOSSY COMPRESSION
Abdou Youssef
-
Motivation for Transforms
-
Desirable Transforms
-
Different Perspectives of Transforms
-
Matrix Formulation of Transforms
-
Transform-Based Lossy Compression
-
The Matrix of the Fourier Transform
-
The Matrix of the Discrete Cosine Transform (DCT)
-
The Matrix of the Hadamard Transform
-
The Matrix of the Walsh Transform
-
The Matrix of the Haar Transform
-
Vector Space Perspective
-
Relationship between the Vector Basis
and the Matrix Formulation of Transforms
-
Visualization of Basis Images of the Various
Transforms
-
Frequency Perspective: The Fourier Transform
-
Connection with The Human Visual System
-
Connection to Compression
-
Treatment of Discrete Signals (Discrete Fourier Transform)
-
Why Use DCT rather than DFT (Boundary Problems of the Fourier Transforms)
-
Relation of DCT to FFT
-
Statistical Perspective
-
DCT vs. KL
Back to Top
1. Motivation for Transforms
- Why transform the data
- To decorrelate the data so that fast scalar
(rather than slow vector) quantization can be used
- To exploit better the characteristics of the human visual system
(HVS) by separating the data into vision-sensitive parts
and vision-insensitive parts
- To compact most of the ``energy'' in a few coefficients, so that
to discard most of the coefficients and thus achieve compression
Back to Top
2. Desirable Transforms
- Desirable Properties of transforms
- Data Decorrelation, exploitation of HVS, and energy compaction
- Data-Independence (same transform for all data)
- Speed
- Separability (for fast transform of multidimensional data)
- Various transforms achieve those properties to various extents
- Fourier Transform
- Discrete Cosine Transform (DCT)
- Other Fourier-like transforms: Haar, Walsh, Hadamard
- Wavelet transforms
- The Karhunen-Loeve Transform
- Optimal w.r.t. data decorrelation and energy compaction
- But it is data-dependent
(the transform matrix is different for different matrices)
- And slow because the transform matrix has to be computed every time
- Therefore, KL is only of theoretical interest to data compression
Back to Top
3. Different Perspectives of Transforms
- Statistical perspective
- Frequency perspective
- Vector space perspective
- End-use perspective (matrix formulation)
Back to Top
4. Matrix Formulation of Transforms
- Simply stated, a transform is a matrix multiplication of
the input signal and the transform-matrix
- Each of the standard transforms mentioned earlier is
defined by an N×N square non-singular matrix AN
- Transform of a 1D discrete input signal (a column vector x of N
components) is the computation of y=ANx
- Transform of an N×M image X is transform of
each column followed
by transform of each row. In matrix form, transform of image X
is the computation of Y=ANXAMt
- The inverse transform is simply x=AN-1y for 1D signals, and
X=AN-1Y(AM-1)t for images
Back to Top
5. Transform-Based Lossy Compression
- Compression of an image X:
- Transform X, yielding Y=ANXAMt
- Scalar-quantize Y, yielding Y'
- Losslessly compress Y', yielding a bit stream B
- Image reconstruction
- Losslessly decompress B back to Y'
- Dequantize Y', yielding an approximation Y" of Y
- Inverse-transform Y" yielding a reconstructed image
X'=AN-1Y"{AM-1}t.
- Except for the case of the KL transform, the
characterizing matrix AN of each of the standard transforms
is independent of the input, that is, AN is the same for
all 1D signals and images.
- In the following, the matrix AN of each transform will
be defined for arbitrary N, and then A2, A4 and A8
will be shown
Back to Top
6. The Matrix of the Fourier Transform
Back to Top
7. The Matrix of
the Discrete Cosine Transform (DCT)
- The matrix AN=(akl) for DCT:


- Remark: AN-1=ANt
- Illustrations:

Back to Top
8. The Matrix of the Hadamard Transform
- The matrix AN=(akr) for the Hadamard Transform is defined
as follows:
- Let k=kn-1kn-2...k0 in binary
- Let r=rn-1rn-2...r0 in binary
- akr =
 (-1) kn-1.rn-1+
kn-2.rn-2 + ... +
k0.r0
(-1) kn-1.rn-1+
kn-2.rn-2 + ... +
k0.r0
- Alternatively, the Hadamard matrix can be defined recursively:


- Remark: AN-1=ANt=AN
- Illustrations:
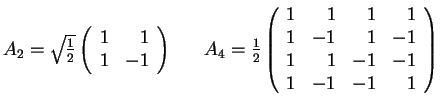

Back to Top
9. The Matrix of the Walsh Transform
- The matrix AN=(akr) for the Walsh Transform is defined
as follows:
- Let k=kn-1kn-2...k0 in binary
- Let r=rn-1rn-2...r0 in binary
- akr =
 (-1) kn-1.r0+
kn-2.r1 + ... +
k0.rn-1
(-1) kn-1.r0+
kn-2.r1 + ... +
k0.rn-1
- Remark: AN-1=ANt=AN
- Illustrations:
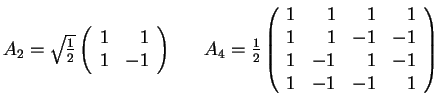

Back to Top
10. The Matrix of the Haar Transform
- The matrix AN=(akl) for the Haar Transform, where N=2n:


- Illustrations:

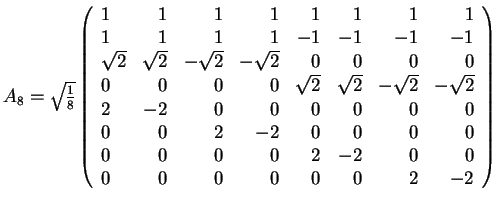
Back to Top
11. Vector Space Perspective
- Analog signals are treated as an infinite-dimensional functional
vector space
- Finite Discrete are signals treated as finite-dimensional vector
spaces
- In either case, the vector space has a basis
{ek | k=0,1,...}
- In fact, the vector space can have multiple bases (plural of basis).
- A transform of a signal x is a change of basis, that is, a linear decomposition of x
along a second basis:
- Suppose that we have two bases, an original one {ek | k=0,1,...}
and a new one {fk | k=0,1,...}
- suppose that the originial basis {ek | k=0,1,...}
was used to express the "natural" components of x:
x=x0e0 +x1e1 +x2e2 + ... ,
- Express x in terms of the new basis: x=y0f0 +y1f1 +y2f2 + ... , where the {yk} are
real/complex numbers
- Transform: x
 (yk)k
(yk)k
- (yk)k is a representation of x, or the "coordinates"
of x in the new coordinate system {fk | k=0,1,...}
- Compression-related desirable properties of a vector-space basis
- Correspondence with the human visual system
- Specifically, only a very small number of basis vectors
are relevant to (i.e., visible by) the HVS, while
the majority of the basis vectors are invisible to the
HVS
- Uncorrelated decomposition-coefficients (yk)k
Back to Top
12. Relationship between the Vector Basis
and the Matrix Formulation of Transforms
- Consider finite 1D discrete signals of N components
- They form an N-dimensional vector space RN,
where every vector is a column vector
- Any basis consists of N linearly independent column vectors
e0,e1, ... ,eN-1
- The canonical basis is:
e0,e1, ... ,eN-1 where
e0=(1,0,0,...,0)t,
e1=(0,1,0,...,0)t,
... ,
eN-1=(0,...,0,1)t
- For any signal x=(x0 x1 ... xN-1)t,
x=x0e0+x1e1+...+xN-1eN-1
- if we use a different basis
f0,f1, ... ,fN-1, and express x along
this new basis, then
x=y0f0+y1f1+...+yN-1fN-1
- That is,
(x0 x1 ... xN-1)t=
(f0 f1 ... fN-1)
(y0 y1 ... yN-1)t
- In Matrix form, let
- B=(f0 f1 ... fN-1), an N x N matrix,
where every basis vector fj is expressed as a vector in the original
coordinate system
e0,e1, ... ,eN-1, that is,
fj=a0je0+a1je1+...+
aijei+...+aN-1,jeN-1=(a0j
a1j ... aN-1,j)t
- A=B-1
- y= (y0 y1 ... yN-1)t, an N-dimensional column vector
- x=(x0 x1 ... xN-1
)t,
an N-dimensional column vector
Therefore, the equation of item 6 above is expressed as:
x=By
- Equivalently,
y=Ax,
where the columns of A-1
are the basis column vectors
f0, f1, ... , fN-1
- Consider now N×M images
- They form an NM-dimensional vector space RN×M
- Any basis consists of NM matrices Ekl of
dimensions N×M
- Following the same analysis as above, a transform
basis
Ekr= (column k of AN-1).(column r of AM-1)t
= ek.ert
for k=0,1,...,N-1 and l=0,1,...,M-1
- I=
 JklEkl over all k and l.
JklEkl over all k and l.
- Remark: For analog signals, the vector space is infinite-dimensional,
and its basis is the infinite set of sine and cosine waves, to
be addressed later
Back to Top
13. Visualization of Basis Images of the Various Transforms
- The real part of the basis vectors of FFT for N=8

- The basis vectors of DCT for N=8

- The basis vectors of Hadamard transform for N=8

- The basis vectors of Haar transform for N=8

Back to Top
14. Frequency Perspective: The Fourier Transform
Back to Top
15. Connection with The Human Visual System
- In
 , the frequencies are
k/T for all integers k
, the frequencies are
k/T for all integers k
- The higher |k|, the higher the frequency
- In
 , yk is the k-th
frequency content of x(t)
, yk is the k-th
frequency content of x(t)
- Experiments have shown that
- suppressing a yk (along with y-k) for any high frequency
k causes HARDLY VISIBLE or NO VISIBLE change to x(t)
- suppressing a yk (along with y-k) for some low frequency
k causes VISIBLE changes to x(t)
- 1D Illustration: Notice the minor changes in shape of the plots as
high frequencies are dropped, and the big change when the lowest frequency
is dropped

- Another Illustration: Decreasing ability to resolve (detect)
changes/differences/contrast at increasingly higher frequencies:

- A Third Illustration: Decreasing ability to resolve (detect)
changes/differences/contrast at increasingly lower frequencies, keeping the "field
of view" constant ([0 pi]):

- Thus, the HVS is sensitive to moderate-to-low frequency data but insensitive to
high-frequency data or very low frequency data
Back to Top
16. Connection to Compression ("First Cut")
- Facts
-
 is a good mathematical and visual approximation of x(t)
is a good mathematical and visual approximation of x(t)
- The faster the decay of yk, the smaller r can be
- Thus,
 is a very small approximate
representation of x, leading to high compression
is a very small approximate
representation of x, leading to high compression
Back to Top
17. Treatment of Discrete Signals (Discrete Fourier Transform)
- Sample N values (xl) of x(t) at N points:
 for l=0,1,...,N-1.
for l=0,1,...,N-1.
-

- Since (xl) is discrete and finite, there is no need to keep an
 of yk's; rather, y0,y1,...,yN-1 are sufficient. That is,
of yk's; rather, y0,y1,...,yN-1 are sufficient. That is,
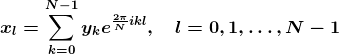

- DFT:

- Put in matrix form:

- Again, for large k, yk can be suppressed or heavily quantized
Back to Top
18. Why Use DCT rather than DFT (Boundary Problems of the Fourier Transforms)
- Discontinuities at the boundaries cause large high-frequency contents
- Eliminating those frequency contents cause boundary artifacts (known
as Gibbs phenomenon, ringing, echoing, etc.)
Back to Top
19. Relation of DCT to FFT
- Let (xk) be an original signal, and (yk) its DCT transform,
k=0,1,...,N-1
- Shuffle x to become almost symmetric; that is, create
a new signal (x'l) by taking the even-indexed terms followed
by the reverse of the odd-indexed terms:
- x'k=x2k and x'N-k-1=x2k+1, for k=0,1,...,N/2-1
- y'=DFT(x');
- yk=
 Real(y'k),
k=1,2,...,N-1
Real(y'k),
k=1,2,...,N-1
Back to Top
20. Statistical Perspective
- Decorrelation of data leads to energy compaction, that is, concentrating the
visual contents into a few coefficients.
- Decorrelation of data minimizes the distortions caused by scalar
quantization
- The Karhunen-Loeve (KL) transform decorrelates the signal data completely,
and thus compacts the energy into the minimum number of coefficients
- The MSEk between the original signal and the one reconstructed from
the k most important coefficients of a transform is minimized if
the transform is KL
- Drawback of KL: the transform matrix is data-dependent, that is, for each
new signal X, the transform matrix A is different and depends on
the statistical properties of X.
- KL is a costly ideal for decorrelation/energy compaction/minimization of MSE
- For other transforms, the more a transform decorrelates the data, the better
the energy compaction and compression performance
- DCT does a good job in decorrelation:

Back to Top
21. DCT vs. KL
- For most natural signals, the KL basis and the DCT basis
are almost identical
- Therefore, DCT is near optimal (in decorrelation, energy
compaction, and rme distortion) because KL is optimal
- Unlike KL, DCT is not signal-dependent
- Hence the popularity of DCT
Back to Top




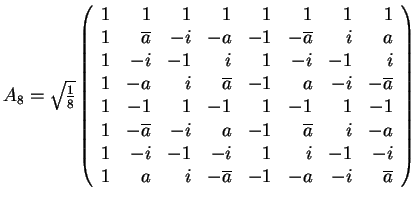




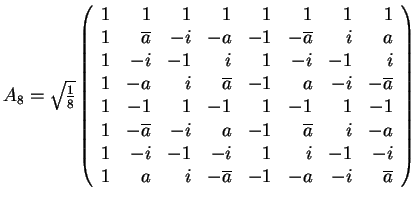



 (-1) kn-1.rn-1+
kn-2.rn-2 + ... +
k0.r0
(-1) kn-1.rn-1+
kn-2.rn-2 + ... +
k0.r0


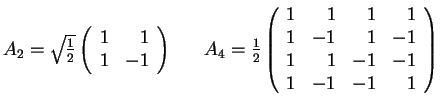

 (-1) kn-1.r0+
kn-2.r1 + ... +
k0.rn-1
(-1) kn-1.r0+
kn-2.r1 + ... +
k0.rn-1
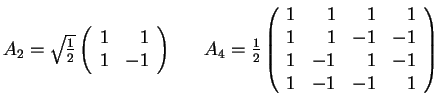




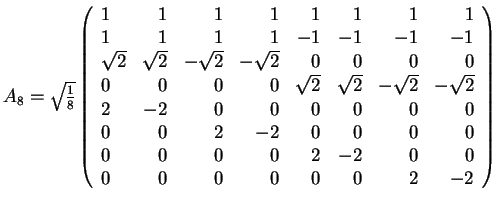
 (yk)k
(yk)k
 JklEkl over all k and l.
JklEkl over all k and l.






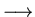 (yk)k
(yk)k

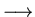 0 as |k|
0 as |k| 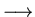
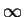
 is periodic of period T. Thus, even if x(t) is defined
over [0,T] only, the Fourier series ``periodizes'' x(t)
is periodic of period T. Thus, even if x(t) is defined
over [0,T] only, the Fourier series ``periodizes'' x(t)
 , the frequencies are
k/T for all integers k
, the frequencies are
k/T for all integers k
 , yk is the k-th
frequency content of x(t)
, yk is the k-th
frequency content of x(t)




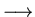 0 as |k|
0 as |k| 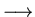
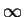
 is a good mathematical and visual approximation of x(t)
is a good mathematical and visual approximation of x(t)
 is a very small approximate
representation of x, leading to high compression
is a very small approximate
representation of x, leading to high compression
 for l=0,1,...,N-1.
for l=0,1,...,N-1.

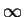 of yk's; rather, y0,y1,...,yN-1 are sufficient. That is,
of yk's; rather, y0,y1,...,yN-1 are sufficient. That is,
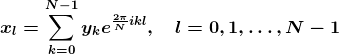



 Real(y'k),
k=1,2,...,N-1
Real(y'k),
k=1,2,...,N-1
