INTRODUCTION AND BACKGROUND
Abdou Youssef
-
INTRODUCTION
-
NEED/MOTIVATION FOR COMPRESSION
-
BASIC DEFINITIONS
-
STRATEGIES FOR COMPRESSION
-
INFORMATION THEORY PRELIMINARIES
1. INTRODUCTION
- What is Compression?
- It is a process of deriving more compact (i.e., smaller)
representations of data
- Goal of Compression
- Significant reduction in the data size to reduce the
storage/bandwidth requirements
- Constraints on Compression
- Perfect or near-perfect reconstruction (lossless/lossy)
- Strategies for Compression
- Reducing redundancies
- Exploiting the characteristics of human vision
Back to Top
2. NEED/MOTIVATION FOR COMPRESSION
- Massive Amounts of Data Involved in Storage/Transmission of
Text, Sound, Images, and Videos in Many Applications
- Applications
- Medical imaging
- Teleradiology
- Space/Satellite imaging
- Multimedia
- Digital Video: entertainment, home use
- Digital photography
- Concrete Figures
- A typical hospital generates terabytes of data per year
- NASA's earth orbiters generate terabytes of data per day
- One 2-hour HD video = (1920 width x 1080 height) x 30 fps x 60 seconds x 60 minutes x 2 hours
= 448 Giga pixels = 1.343 TBytes
- HD-video data rate per second = (1920 width x 1080 height) x 30 fps x 24 bits/pixel= 1.5 Gb/s
- With MPEG2 High (80Mb/s), need compression ratio of 18.66:1
- With DVD MPEG2 (9.8Mb/s), need compression ratio of 152:1 (unless it is stored at 480 pixels in height)
- For Ultra High definition (4K/5K/6K/8K UHD), the amounts of data are much larger. For example, in Super Hi-Vision specifications (Japan), the uncompressed video bit rate is 144Gb/s (100 times bigger than HD)
Back to Top
3. BASIC DEFINITIONS in Compression/Coding
- Coding : Compression
- Codeword: A binary string representing either the whole coded data
or one coded data symbol
- Coded Bitstream: the binary string representing the whole coded data.
- Lossless Compression: 100% accurate reconstruction of the original data
- Lossy Compression: The reconstruction involves errors
which may or may not be tolerable
- Bit Rate: Average number of bits per original data element after compression
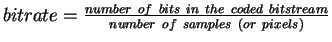
-
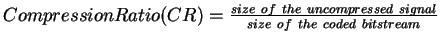
- Signal-to-Noise Ratio (SNR) in the case of lossy compression.
Let I be an original signal (e.g., an image), and
R be its lossily reconstructed
counterpart. SNR is defined to be:
SNR=10 log10 (||I||2/||I-R||2) = 20 log10 (||I||/||I-R||)
where for any vector/matrix/set of number E={x1, x2, ... , xN},
||E||2=x12 + x22 + ... + xN2.
- The unit of SNR is "decibel" (or dB for short).
- So, if SNR = 23, we say the SNR is 23 dB.
-
Mean-Square Error (MSE): ||I-R||2/N
-
Relative Mean-Square Error (RMSE): ||I-R||2/||I||2
-
Therefore, SNR = -10 log10 RMSE.
- So the smaller the error, the higher the SNR. In particular, the higher the SNR, the better the quality of the reconstructed data.
- Exercise: Prove that if RMSE is decreased by a factor of 10, then SNR increases by 10 decibels.
- It is this nice fact that justifies the multiplicative factor in the definition of the SNR.
Back to Top
4. BASIC IMAGE/VIDEO/SOUND DEFINITIONS
-
An image is a matrix of numbers, each number called a pixel (short for picture element)
- A binary image (or black-and-white B/W image) is an image where every pixel can have one of two values only (typically 0 and 1).
- A grayscale image is a non-color image but there various shades of gray. That is what we typically refer to informally when we talk aboiut the (old) back-and-white TVs/cameras/photos.
- A color image is an image where every pixel can have a color.
- Theorem (Newton): Every color is a combination of three colors (such as Red, Green and Blue), called the basic colors.
- Therefore, in color images, every pixel is represented with three (numerical) components, such as (R,G,B),
where R represents how much red there is in that pixel, G how much green, and B how much blue.
- The spatial resolution of an image is:
- the total number of pixels in the image (like you hear a megapixel image,
or a 6-megapixel camera, ...); or
- the number of pixels per row and per column, like when one says this image is an 1080x1920 image, which means it has 1080 rows and 1920 columns, which also means that every row has 1920 pixels and every column has 1080 pixels, that is, the image has height 1080 pixels and width 1920 pixels; or
- number of pixels per inch; for binary images (like in fax machines, basic scanners, and old
dot-matrix printers), it is called "dot per inch (dpi)".
- Note: For a fixed physical size image, the higher the spatial resolution, the more (and smaller) the pixels are, and thus the better the quality (and detail) of the image.
- The density resolution (or bit depth) is the number of bits per pixel. The higher
the density resolution, the more colors (or shades of gray) can be represented, and thus
the crisper or more detailed the image is.
- A video is a sequence of images. Every image in the sequence is called a frame.
- A video is captured/displayed at a certain rate, called the
frame rate, measured in terms of frames per second (fps).
- A typical rate that does not show jerkiness is 30 fps. For higher definition (of motion), the rate can be higher. Lowere rates, likes 20 fps and even 15 fps, were used before when communications and computers were slower.
- Lower than 15 fps rates would be quite jerky and unacceptable.
- Resolutions of various technologies:
- Standard definition (SD): Height = 576 or 480 pixels, Width = 768 or 640 pixels
- High definition (HD): H = 1080 p, W = 1920 p
- 4K ultra high definition (4K UHD): H = 2160 p, W =3840 p
- 5K ultra high definition (5K UHD): H = 2880 p, W = 5120 p
- 6K ultra high definition (6K UHD): H = 3456 p, W =6144 p
- 8K ultra high definition (4K UHD): H = 4320 p, W = 7680 p
- Note: UHD allows for frame rates of up to 120 fps, and the density resolution is 8 or 10 or 12 bits per color (i.e., 24 or 30 or 36 bits per pixel)
- A sound/audio (digital) signal is a sequence of values, called
samples,
where every sample is the intensity of the recorded sound at the corresponding moment in time.
- The sampling rate of a sound is the number of samples per second.
- The CD quality sampling rate is 44.1K samples per second (or 44.1 KHz),
usually at 16 bits per sample, though 24 bits per sample is now common.
- In digital sound used for miniDV, digital TV, and DVD, the sampling rate is 48 KHz.
- In DVD-Audio and in Blu-ray audio tracks, the sampling rate is 96 KHz or 192 KHz.
- In the UHD Super Hi-Vision specifications:
- Sampling rate: 48/96 kHz
- Bit length: 16/20/24 bits
- Number of channels: 24
- When the sampling rate is infinity, the signal becomes what is called
"analog signal".
- When signal is captured as an analog signal, it can be converted to a digital signal by
an analog-to-digital converter (also called A/D converter or digitizer)
- If a digital signal is fed into a digital-to-analog converter (also called D/A converter), the output is obviously an analog signal.
- Modulators are D/A converters, and demodulators are A/D converters. So, a modem is both an A/D and D/A converter.
Back to Top
5. STRATEGIES FOR COMPRESSION: REDUNDANCY REDUCTION
- Symbol-Level Representation Redundancy
- Different symbols occur with different frequencies
- Variable-length codes vs. fixed-length codes
- Frequent symbols are better coded with short codes
- Infrequent symbols are coded with long codes
- Example Techniques: Huffman Coding
- Block-Level Representation Redundancy
- Different blocks of data occur with varying frequencies
- Better then to code blocks than individual symbols
- The block size can be fixed or variable
- The block-code size can be fixed or variable
- Frequent blocks are better coded with short codes
- Example techniques: Block-oriented Huffman, Run-Length
Encoding (RLE), Arithmetic Coding, Lempil-Ziv (LZ)
- Inter-Pixel Spatial Redundancy
- Neighboring pixels tend to have similar values
- Neighboring pixels tend to exhibit high correlations
- Techniques: Decorrelation and/or processing in the frequency
domain
- Spatial decorrelation converts correlations into symbol- or
block-redundancy
- Frequency domain processing addresses visual redundancy
(see below)
- Inter-Pixel Temporal Redundancy (in Video)
- Often, the majority of corresponding pixels in successive
video-frames are identical over long spans of frames
- Due to motion, blocks of pixels change in position but not
in values between successive frames
- Thus, block-oriented motion-compensated redundancy reduction
techniques are used for video compression
- Visual Redundancy
- The human visual system (HVS) has certain limitations
that make many image contents invisible.
Those contents, termed visually redundant, are the target
of removal in lossy compression.
- In fact, the HVS can see within a small range of spatial frequencies: 1-60 cycles/arc-degree
- The graph below plots the contrast sensitivity function (CSF) as a function of frequency (number of black stripes per unit length). It measures how well we can tell black stripes apart (assuming a white background), depending on the density of stripes (i.e., depending on how close the stripes are to one another).
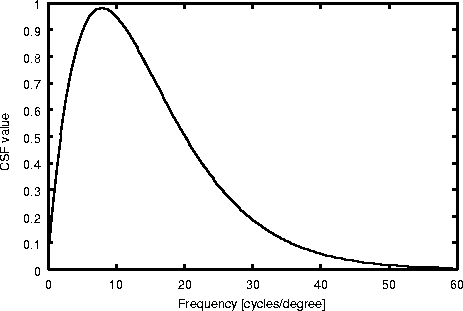
- To understand the frequencies better in the plot, we'll translate the frequencies from nymber of cycles per degree to number of stripes per inch.
- A full circle is 360 degrees. At a viewing distance of R inches (i.e., a circle of radius R), the length (in inches) of one degree is:
Length of one arc degree=2πR/360 =
2*3.14*R/360 = 0.0175R inches
1 cycle/degree = 360/(2πR) stripes per inch
- For example, at viewing distance R = 10 feet = 120 inches, the length of 1 degree is 0.0175*120=2.1 inches, and 1 cycle/degree=0.4775 stripes per inch.
- Therefore, a frequency of 8 cycles per degree translates to 8/2.1 stripes per inch= 3.8 stripes per inch. Some more translations (under R=120 inches):
- 1 cycle per degree = 0.48 stripes per inch
- 8 cycles per degree = 3.8 stripes per inch
- 10 cycles per degree = 4.76 stripes per inch
- 20 cycles per degree = 9.52 stripes per inch
- 30 cycles per degree = 14.28 stripes per inch
- 40 cycles per degree = 19.05 stripes per inch
- 50 cycles per degree = 23.81 stripes per inch
- 60 cycles per degree = 28.57 stripes per inch
- The CSF graph shows that, on average, a person is most sensitive to contrast at 8 cycles/degree, i.e., when we have 3.8 stripes per inch at a viewing distance of 10 feet.
- It also shows that beyond 28 stripes per inch, we cannot tell the stripes apart (the stripes will appear fused into a continuous blob of gray), from a viewing distance of 10 feet.
- Approach for reducing visual redundancy in lossy compression
- Transform: Convert the data to the frequency domain
- Quantize: Under-represent the high frequencies
- Losslessly compress the quantized data
Back to Top
6. INFORMATION THEORY PRELIMINARIES
- Discrete Memoryless Source S: A data generator where the alphabet
is finite and the symbols generated are independent of
one another. Assume the alphabet is {a1,a2,...,an}
- Let pk = Probability that symbol ak is generated
(transmitted) by the source
- Entropy: H(S) = – (p1log p1 +
p2log p2 + ... + pnlog pn)
- Theorem (Shannon): H(S) is the minimum average number of bits/symbol possible
That is, no matter which lossless compression is ever invented, its bitrate can never be better (smaller)
than H(S) for any memoryless source S.
- Sources with Memory: Presence of inter-symbol correlation
- Their entropy is still the min average number of bits/symbol
- Adjoint Source of Order N
- Treat each possible block A of N symbols as a
macrosymbol, and compute the probability PA
- Treat the source as a memoryless source consisting of
the macrosymbols A's and their probabilities PA
- The entropy
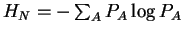
- Theorem (Shannon): For any source S with memory,
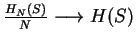 as N
as N 
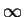
- This implies that for any source S with memory (i.e., with inter-symbol correlation/redundancy),
if we divide it into blocks of large enough size and then block-code it without taking advantage of
inter-block correlation, then we can approximate the performance of any other coder for the source.
Back to Top
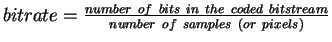
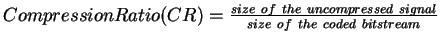

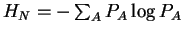
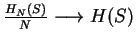 as N
as N