Motivation for Standards
- Why Standards?
- Compatibility
- Production cost reduction
- Triggering growth and product development
- Do JPEG/MPEG standards kill research?
- Not necessarily
- Those standards are very flexible regarding the encoder design, leaving much room for improvement
- The trends are toward even greater flexibility in future generations of the standards
- Another growth area is the development of systems which integrate components that use the standards
Image/Video Compression Standards (Outline)
- JPEG
- Baseline JPEG
- Extended JPEG
- Lossless JPEG (DPCM + Huffman/Arithmetic)
- MPEG
- History (H.261 and H.263)
- MPEG1
- MPEG2
- Why not MPEG3
- MPEG4
The JPEG ``Toolkit''
- JPEG provides a ``toolkit'' of techniques for compressing continuous-tone,
still, color and monochrome images
- Baseline JPEG provides a DCT-based algorithm, and uses
run-length encoding and Huffman coding
- Baseline JPEG operates only in sequential mode, and is restricted to
8 bits/pixel input images
- Extended JPEG offers several optional enhancements:
- 12-bit/pixel input
- Progressive transmission
- Choice between Arithmetic and Huffman coding
- Adaptive quantization
- Tiling
- Still picture interchange file format (SPIFF)
- Selective refinement
- Applications of JPEG
- Desktop publishing, color fax, photojournalism, medical images, general image archiving systems, consumer imaging, graphic arts, and others
The Baseline JPEG Algorithm
- It operates on 8×8 blocks of the input image
- Mean-normalization (subtract 128 from each pixel)
- Transform: DCT-transform each block
- Quantization
- An 8×8 quantization matrix Q is user-provided
- Each block is divided by Q (point by point)
- The terms are then rounded to their nearest integers
- Remark: Up to 4 quantization matrices per image are allowed (for example, one for luminance, and for each of the three color components)
- Entropy-coding of the DC coefficients (the top left coefficient of each quantized block) using DPCM+Huffman
- Huffman-encode the DC residuals derived from the difference between each DC and the DC of the preceding block
- Entropy-coding of the AC (i.e., non-DC) coefficients
- Zigzag-order the quantized coefficients of each block
- Record for each nonzero coefficient both its distance (called run) to the preceding nonzero coefficient in the zigzag sequence, and its value (called level)
- Huffman code the [run,level] terms using one single Huffman table for all the AC's of the image
The Quantization Matrices
- They are user-provided
- They can be computed using the contrast sensitivity
function of the HVS
- Their values are 8-bit integers
- They provide control over the bitrate by scaling them by a constant
factor
- Example of Q:
16 11 10 16 24 40 51 61 12 12 14 19 26 58 60 55 14 13 16 24 40 57 69 56 14 17 22 29 51 87 80 62 18 22 37 56 68 109 103 77 24 35 55 64 81 104 113 92 49 64 78 87 103 121 120 101 72 92 95 98 112 100 103 99
Coding of the DC Residuals
- The DC residuals are in the range [-2047,2047]
- Thus, the magnitude of each residual is between 0 and 2047=211-1, inclusive.
- Divide this range into 12 subranges, or categories, where category k ranges from 2k-1 to 2k-1 inclusive. (Note that category 0 has only the integer 0).
- Let r be a DC residual. Clearly, |r| = 2k-1 + t, where 0 <= t <= 2k-1-1. In particular, t can be represented in binary using k-1 bits.
- Therefore, r can be uniquely represented by s, k, and t.
- Develop a Huffman code for the 12 categories, where every codeword
is at most 16 bits long
- Encode each DC residual r as a binary string hsm where
- h is the codeword of the residual's category k
- s= sign of the residual; s=0 if negative, 1 if positive
- m= the (k-1)-bit binary representation of t.
Coding of the AC Terms (The AC Huffman Table)
- All non-zero AC terms are of magnitude <= 210-1
- Let x be an AC term, and let d be the length of the zero run between x and the previous nonzero AC term.
- 1 <= |x| <= 210-1
- Divide the range 1 .. 210-1 into 10 categories, where category k is the range (2k-1 .. 2k-1) inclusive.
- Represent x by its sign s and its magnitude |x|. s = 0 if x<0, 1 otherwise.
- For whatever value of |x|, there is a unique k such that 2k-1 <= |x| <= 2k-1. k is the category of x
- |x| = 2k-1 + t, where 0 <= t <= 2k-1-1. In particular, t can be represented in binary using k-1 bits.
- Therefore, x can be uniquely represented by s, k, and t.
- Thus, (d,x) can be represented by (d,k,s,t), where s is one bit and t is k-1 bits.
- The runlength d is between 0 and 63.
- d = 15p + r, where r=0,1,2,...,14.
- r can be represented with 4 bits r3r2r1r0, different from 1111.
- p can be represented with 111100001 111100002 ... 1111000p
- This implies that d is 111100001 111100002 ... 1111000pr3r2r1r0
- the category (or level) k, being between 1 and 10, can be represented with 4 bits k3k2k1k0.
- Therefore, the (d,k) in the (d,k,s,t) representation of (d,x), is represented as
111100001 111100002 ... 1111000pr3r2r1r0k3k2k1k0 - This representation of (d,k) can be viewed as a sequence of p+1 bytes.
- The last byte represents 16*10= 160 legitimate values
- Add to those the byte 11110000 and the end-of-block (EOB) symbol to signal the end of the nonzero AC terms in a block.
- This results in 162 different symbols.
- Build a Huffman table for those 162 symbols,
where every codeword is at most 16 bits long
- JPEG encodes each quantized AC term (d,x)=(d,k,s,t) as hsm where
- h is the Huffman codeword of (d,k)
- s= sign of the term; s=0 if negative, 1 if positive
- m= the (k-1)-bit binary representation of t.
Examples
- Take an 8×8 block of Lena B:
143 147 149 152 156 147 146 149 151 146 143 154 148 144 153 132 147 143 145 149 144 145 128 133 152 145 145 144 146 134 130 137 146 143 142 147 124 127 139 138 139 145 139 127 126 135 139 141 145 137 124 130 138 136 140 144 144 124 136 134 137 139 142 145
- Normalize B. It becomes NB=B-128:
15 19 21 24 28 19 18 21 23 18 15 26 20 16 25 4 19 15 17 21 16 17 0 5 24 17 17 16 18 6 2 9 18 15 14 19 -4 -1 11 10 11 17 11 -1 -2 7 11 13 17 9 -4 2 10 8 12 16 16 -4 8 6 9 11 14 17 - Perform DCT, resulting in a block D:
103.4 12.4 6.0 2.1 8.1 5.7 -0.7 -0.4 31.7 11.6 -22.8 -0.7 -0.1 -0.5 -4.7 -1.8 11.0 -21.2 -3.7 8.8 2.3 0.1 -0.2 5.6 0.2 -4.9 10.3 -8.6 -8.9 -2.5 -7.6 -1.4 4.9 -0.4 -1.9 -8.9 6.6 2.6 3.6 3.6 0.7 -0.9 -0.9 4.1 7.2 -15.5 2.8 1.8 -3.1 -1.0 -2.5 -5.5 -5.2 -6.7 10.7 -1.1 -2.9 -0.2 -1.2 -2.7 3.6 2.6 0.4 -6.4
- Quantize (round(D./Q)), resulting in Dq:
6 1 0 0 0 0 0 0 4 1 -2 0 0 0 0 0 1 -2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
- zigzag ordering: 6 1 4 1 1 0 0 -2 -2 allzeros
Example Huffman Table for Lena
| Zero Run | Cetgory | Codelength | Codeword |
|---|---|---|---|
| 0 | 1 | 2 | 00 |
| 0 | 2 | 2 | 01 |
| 0 | 3 | 3 | 100 |
| 0 | 4 | 4 | 1011 |
| 0 | 5 | 5 | 11010 |
| 0 | 6 | 6 | 111000 |
| 0 | 7 | 7 | 1111000 |
| . | . | . | . |
| 1 | 1 | 4 | 1100 |
| 1 | 2 | 6 | 111001 |
| 1 | 3 | 7 | 1111001 |
| 1 | 4 | 9 | 111110110 |
| . | . | . | . |
| 2 | 1 | 5 | 11011 |
| 2 | 2 | 8 | 11111000 |
| . | . | . | . |
| 3 | 1 | 6 | 111010 |
| 3 | 2 | 9 | 111110111 |
| . | . | . | . |
| 4 | 1 | 6 | 111011 |
| 5 | 1 | 7 | 1111010 |
| 6 | 1 | 7 | 1111011 |
| 7 | 1 | 8 | 11111001 |
| 8 | 1 | 8 | 11111010 |
| 9 | 1 | 9 | 111111000 |
| 10 | 1 | 9 | 111111001 |
| 11 | 1 | 9 | 111111010 |
| . | . | . | . |
| . | . | . | . |
| End of Block (EOB) | 4 | 1010 | |
Coding the Example Block
- zigzag ordering: 6 1 4 1 1 0 0 -2 -2 allzeros
- 6 is coded separately along with other DC terms.
- the AC terms are codes as follows:
- the AC terms as a sequence of (d,x) pairs:
(0,1) (0,4) (0,1) (0,1) (2,-2) (0,-2) EOB - As a sequnce of (d,k,s,t), where t is in decimal:
(0,1,1,0) (0,3,1,0) (0,1,1,0) (0,1,1,0) (2,2,0,0) (0,2,0,0) EOB - As a sequnce of (d,k,s,t), where t is in binary using k-1 bits:
(0,1,1,-) (0,3,1,00) (0,1,1,-) (0,1,1,-) (2,2,0,0) (0,2,0,0) EOB - The final code:
00 1 100 1 00 00 1 00 1 11111000 0 0 01 0 0 1010
- the AC terms as a sequence of (d,x) pairs:
- number of bits to code the AC terms: 33 bits
- Bitrate per symbol (out of the 63 AC symbols): 33/36 = 0.52 bits/symbol
- Compression ration based on those ACs alone: (63*8/33)= 15
Decoding
- Entropy-decode the bitstream back to the quantized blocks
- Dequantize: multiply each block coefficient by the corresponding coefficient
of the quantization matrix
- Apply the inverse DCT transform on each block
- Denormalize: add 128 to each coefficient
- Example: Reconstructed block B'
143 147 153 157 157 154 149 145 145 147 151 154 153 149 144 141 146 147 149 149 146 142 137 134 146 146 145 142 139 135 132 130 145 143 140 136 133 131 130 130 141 138 134 131 130 131 134 135 136 134 130 128 129 133 139 142 133 131 127 126 129 135 142 147 - Error block
0 0 -4 -5 -1 -7 -3 4 6 -1 -8 0 -5 -5 9 -9 1 -4 -4 0 -2 3 -9 -1 6 -1 0 2 7 -1 -2 7 1 0 2 11 -9 -4 9 8 -2 7 5 -4 -4 4 5 6 9 3 -6 2 9 3 1 2 11 -7 9 8 8 4 0 -2
- MSE=5.2
Extended JPEG
- Extended JPEG allows for several optional enhancements:
- 12-bit/pixel input
- Arithmetic coding is allowed as an alternative to Huffman coding
- Adaptive quantization: Allows 5-bit scale change to the quantization matrix from one block to another
- SPIFF: A file format that provides for the interchange of compressed image files between different application environments
- Progressive transmission (PT)
- Sequential PT
- Spectral selection
- Successive approximations
- Hierarchical PT (pyramid encoding)
- Sequential PT
- Tiling
- Selective refinement
Performance of JPEG
- Original Lena

- JPEG-compressed Lena at a compression ratio of 12:1

- JPEG-compressed Lena at a compression ratio of 20:1

- JPEG-compressed Lena at a compression ratio of 32:1

MPEG (1 & 2): Basic Concepts
- Video is a sequence of images called frames
- Color
- Three components: red (R), green (G), and blue (B)
- For compatibility with non-colored media, the RGB model
was converted to an equivalent model --- YCbCr
- Y is the luminance component, which was
experimentally determined to be
Y=0.299R+0.587G+0.114B - Cb=B-Y
- Cr=R-Y
- Y is the luminance component, which was
experimentally determined to be
- Y is referred to as luma, and Cb & Cr as chroma
- Every frame is really 3 images: one Y, one Cb and one Cr
- 8 bits/pixel for each of the three color components
- Because human vision is less sensitive to color,
the Cb and Cr images are downsampled by 2
in each dimension (they are quarter the size of Y images)
- Much of MPEG processing is on the basis of a macroblock: A 16×16 luminance block with the two 8×8 associated chroma blocks
Modes of MPEG Compression
- Intraframe compression
- Exploits spatial redundancy only
- Operates on single frames independetly of other frames
- Interframe compression
- Exploits both spatial and temporal redunadancies
- Employs motion estimation (MS) without standardizing any MS algorithm
- Derives motion-compensated predictions of frames
- Finally, it performs JPEG-like compression on the residual frames
Types of Frames in MPEG

- MPEG has 3 types of frames: I, P, and B
- I frames are stricly intra compressed as in JPEG. Their purpose
is to provide random access points to the video
- P frames are motion-compensated forward-predictive-coded frames; they are interframe compressed, and typically provide more
compression than I frames
- B frames are motion-compensated
bidirectionally-predictive-coded
frames; they are interframe compressed, and typically provide
the most compression
- The relative numbers of I, P and B frames are arbitrary
- An I frame must occur at least once every 132 frames to provide user-acceptible speed of random access to various parts of a video
Interframe Compression of P and B Blocks
- A motion-compensated prediction (i.e., approximation) f'
of a P/B frame f is made
- The residual f-f' is then compressed in a JPEG-like style
- Any macroblock of the original frame f may be strictly intra
compressed if its prediction is deemed to be poor
- Issues to be addressed
- Method of strict intra compression
- Method of compressing residual macroblocks
- Motion-compensated prediction
Flowchart of MPEG Compression
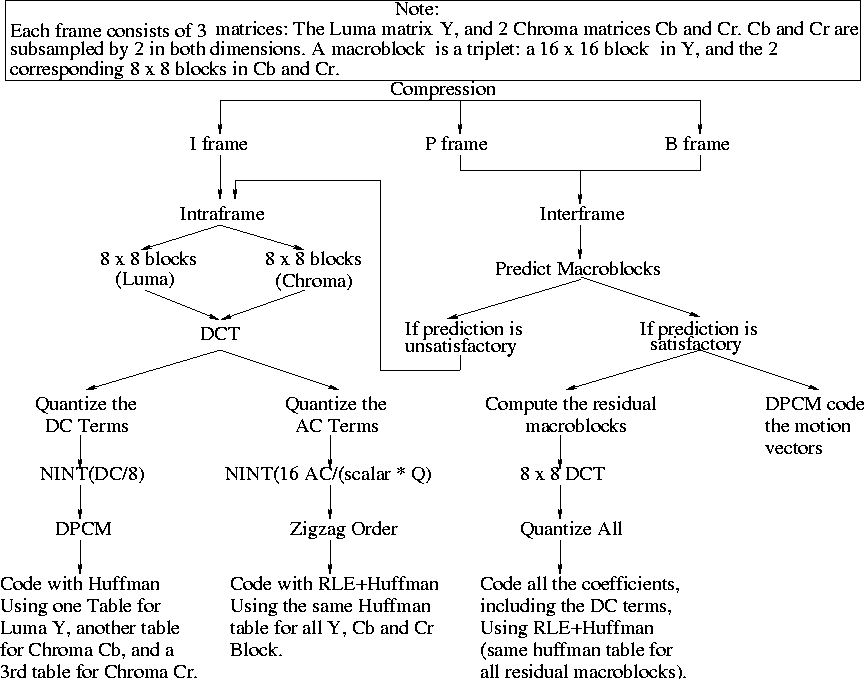
Motion-Estimation and Prediction
- Motion estimation is performed on the basis of macroblocks, using
the 16×16 luminance blocks only
- Motion is assumed to be uniform across all the pixels of a macroblock
- Remark: There is a tradeoff in deciding the size of the basic block for
motion estimation
- The block has to be sufficiently large to avoid ``false hits''
- The block has to be sufficiently small to avoid diverse motions within one single block
- The MPEG block size, 16×16, is a good compromise
Motion-Estimation and Prediction for P Frames

- Consider a P-frame P
- P will be predicted (i.e., approximated) from one single reference
frame R
- R is the most recent (decoded) I or P frame
- For each macroblock MB of P, find the closest matching macroblock MB'
in the reference frame R
- If the MB-to-MB' match is satisfactory, then
- treat MB' as the prediction (i.e., approximation) of MB
- record the motion (i.e., displacement) vector between the two macroblocks (allowing half-pixel accuracy)
- Compute and compress the macroblock residual MB-MB' (luma and chroma)
- If the MB-to-MB' match is found to be unsatisfactory, then
the macroblock MB is strictly intra compressed as is done in I frames
- The motion vectors of all the macroblocks of P exhibit redundancy
due to similar (or sometimes identical) motion experienced by many
neighboring macroblocks
- This redundancy is exploited by coding the consecutive differential
values of motion vectors (i.e., DPCM)
- Remark 1: MPEG does not standardize the decision mechanism for judging
whether or or not a match between two macroblocks is satisfactory
- Remark 2: A typical decision mechanism involves computing an error measure between the luminance of the two macro blocks. The match is treated as satisfory if and only if the error is below a certain threshold. Possible error measures include mean-square error (MSE), mean absolute-difference error (MAD), and variance(MB-MB')/variance(MB).
Motion-Estimation and Prediction for B Frames

- Consider a B-frame B
- B will be predicted (i.e., approximated) from TWO reference
frames R1 and R2
- R1 is the most recent (decoded) past I/P frame, and R2
is the nearest (decoded) future I/P frame
- For each macroblock MB of B, find the closest matching macroblock MB1
in the reference frame R1, and the closest matching macroblock
MB2 in R2
- The predicted macroblock is PM=NINT(alpha1MB1+alpha2MB2)
- alpha1=0.5 and alpha2=0.5 if both matches are satisfactory
- alpha1=1 and alpha2=0 if only the 1st match is satisfactory
- alpha1=0 and alpha2=1 if only the 2nd match is satisfactory
- alpha1=0 and alpha2=0 if neither match is satisfactory
- Compute and compress the macroblock residual MB-PM (luma and chroma)
- If neither match is found to be satisfactory, then
the macroblock MB is strictly intra compressed as is done in I frames
- Record the motion vector(s) between the MB and the other one or two
macroblocks (allowing half-pixel accuracy)
- Again, the motion-vector redundancy is exploited by coding the
consecutive differential values of motion vectors (i.e., DPCM)
- Remark: The prediction mode chosen is 2-bit coded and passed on along with the macroblock header information
MPEG2
- Higher data rates than MPEG1
- MPEG2 allows for higher quality source images
- 4:2:0 (chroma subsamples only horizontally)
- 4:4:4 (no subsampling of chroma)
- Note: 4:2:2 is what's supported by MPEG1
- MPEG2 allows for finer quantization and for specifying
separate quantization table for luma and chroma
- MPEG2 allows for finer adjustment of quantization scale factor,
used in intra compression
- MPEG2 allows for interlaced video
- MPEG2 supports error concealment (of lost macroblocks)
- MPEG2 supports scalable compression
- SNR-scalability: by sending bands of DCT coefficients
- spatial-scalability: pixel resolution by down-/up-sampling
- temporal-scalability: different frame rates by skipping frames
- MPEG2 has a Profile and Level structure
- Profiles are algorithmic elements included in MPEG2
- Levels are upper bounds on parameter values
- Profiles (profiles are backward-compatible)
- Simple: No use of B frames
- Main: what was described earlier, but no scalability
- SNR-scalable
- Spatially scalable
- High: temporally scalable, higher-quality source data (4:2:0, 4:2:2 and possibly 4:4:4 in the future)
- Levels
- Low: 352 × 240 frame size
- Main: 720 × 480 frame size
- High 1440: 1440 × 1152 frame size
- Very High: 1920 × 1080 frame size
References
- B. pennebaker and J. L. Mitchell, JPEG Still Image Data Compression Standard, Van Nostrand reinhold, New York 1993.
- ISO-11172-2: Generic Coding of moving pictures and associated audio (MPEG-1)
- ISO-13818-2: Generic Coding of moving pictures and associated audio (MPEG-2)
Links to other Standards
- JPEG 2000
- An overview of MPEG 4
- MPEG 2/MPEG 4 Audio Coding: Advanced Audio Coding (AAC)
- MPEG 1 Layer 3 Audio (MP3)
- Digital Audio Compression (AC-3) Standard and its 2001 Revision A