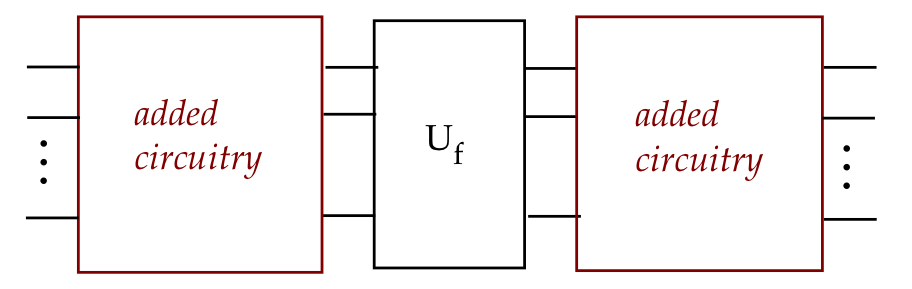
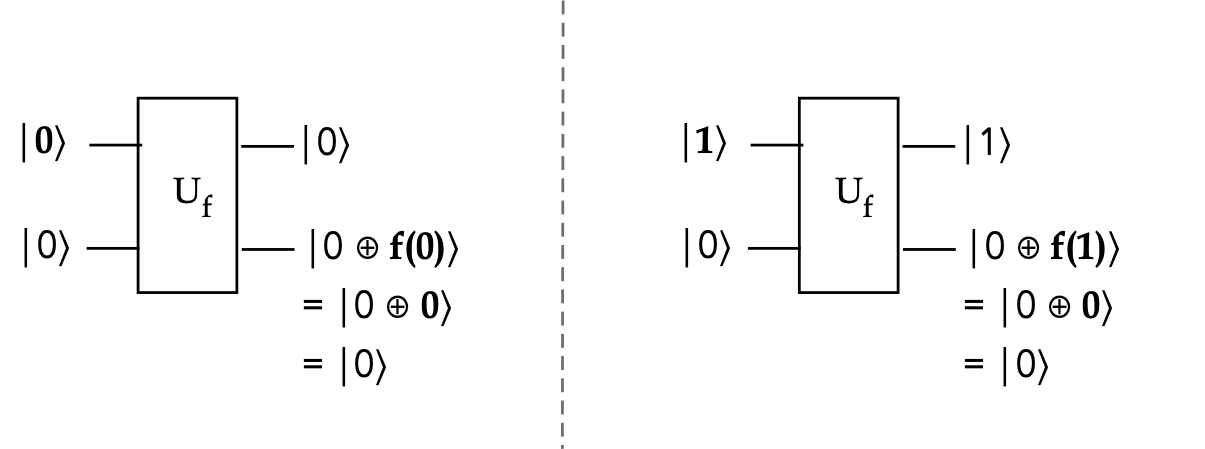
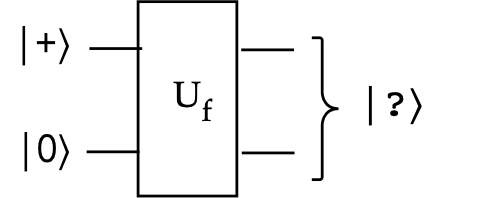
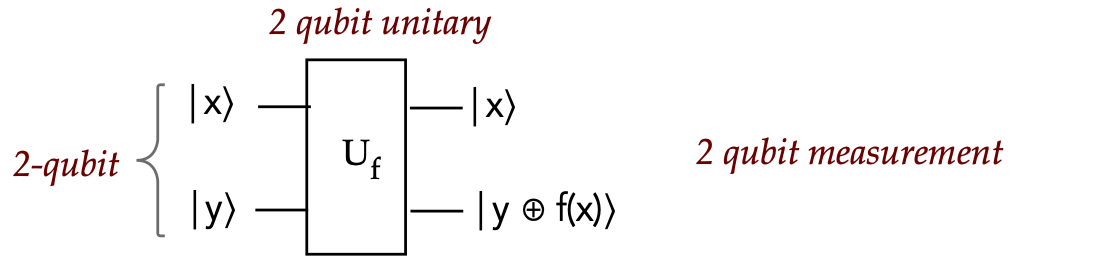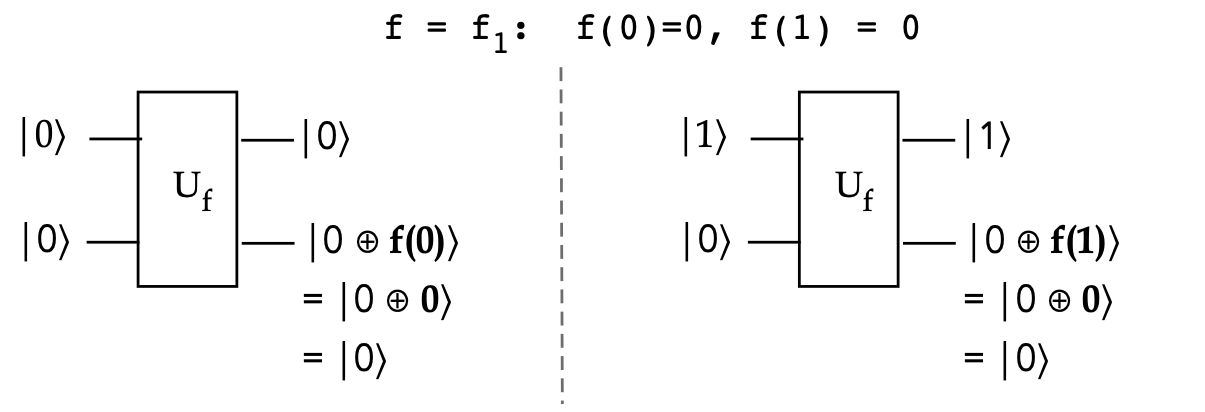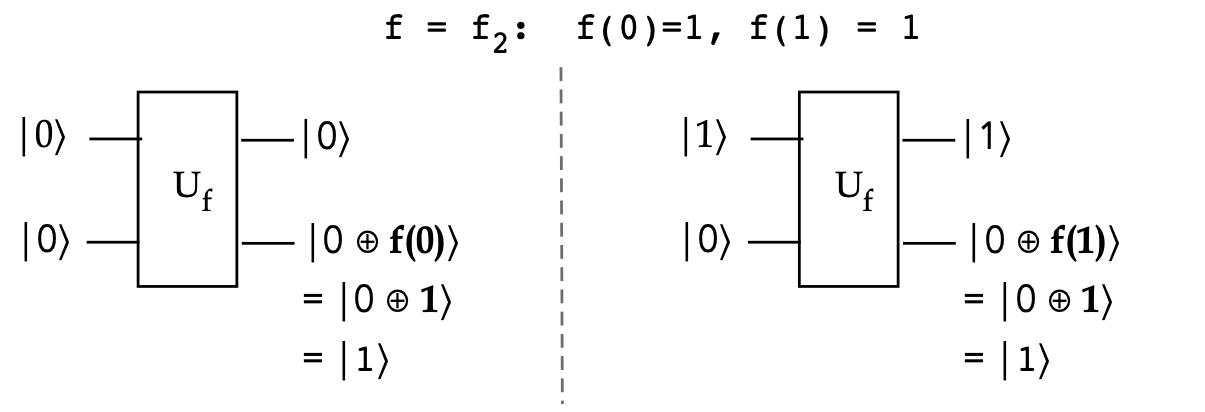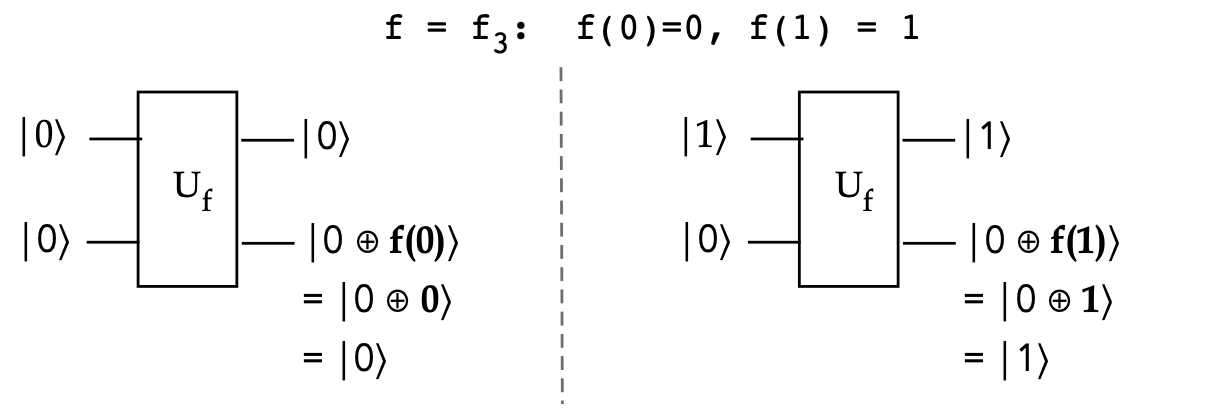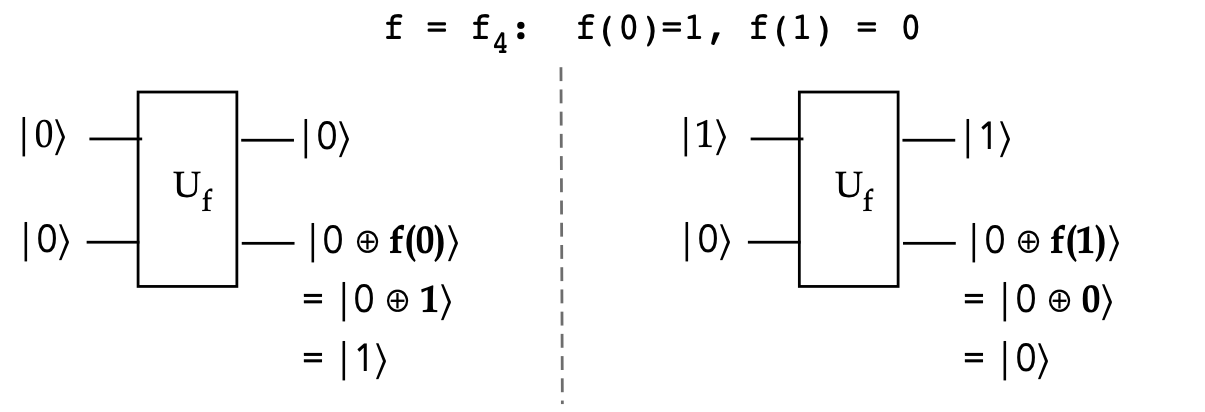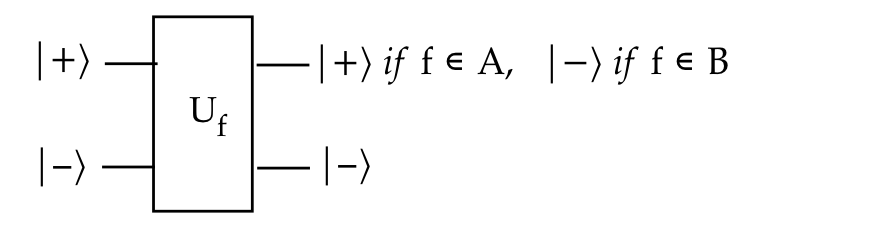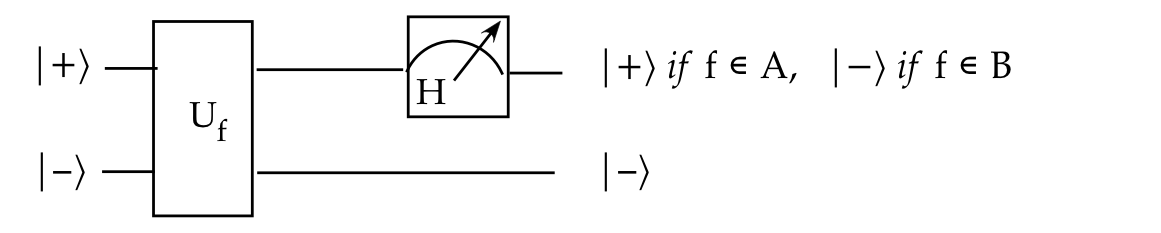Module objectives
The main goals of this module:
- To start down the path of understanding how quantum algorithms work.
- To see how the oracle algorithms, even if impractical,
provide insight into tricks that algorithms use to achieve speed up.
9.1
What is an oracle problem?
First, the motivation:
- In the early days of quantum computing, it was not clear
that any problem existed for which quantum computing would show
a clear improvement over classical.
- Thus, there began a "hunt" for simple problems that
could somehow show significant speed up using quantum algorithms.
- In the first wave of results, a number of artificial
problems were created to demonstrate this potential speed up.
\(\rhd\)
These are the oracle problems.
- Even though the problems aren't useful in practice, the
algorithms use techniques that can be used for practical problems.
\(\rhd\)
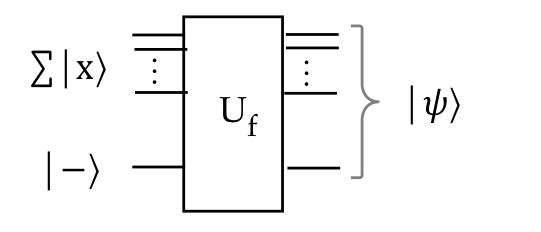
One example: using the all-superposition vector as input
What is an oracle problem?
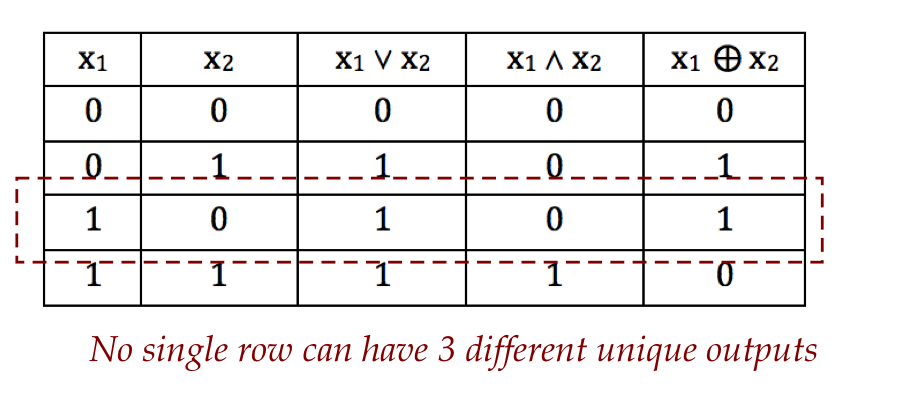
In-Class Exercise 1:
Suppose \(f(x)=f(x_1,x_2,x_3)\) is a 3-input Boolean function that
falls into one of two categories:
- \(f\) is constant, meaning either \(f(x)=0\) or
\(f(x)=1\) for all \(x\).
- \(f\) is balanced, meaning \(f(x)=0\) for exactly
half the inputs (4 input combinations in this case), but we don't know
which ones.
How many trials are needed to determine which category an
unknown \(f\) falls in?
What is the quantum equivalent of an oracle problem?
Such oracle problems are quite artificial but their impact
has been significant:
- It at least shows cases where quantum algorithms are
exponentially faster.
- The techniques used in the algorithms can be analyzed
for application to practical problems.
- One such problem, Simon's problem, inspired a very
practical breakthrough: Shor's integer factoring algorithm.
9.2
Deutsch's algorithm
Deutsch's problem tries to boil down the quantum-classical
difference to a single bit:
- There are only four possible single-bit functions:
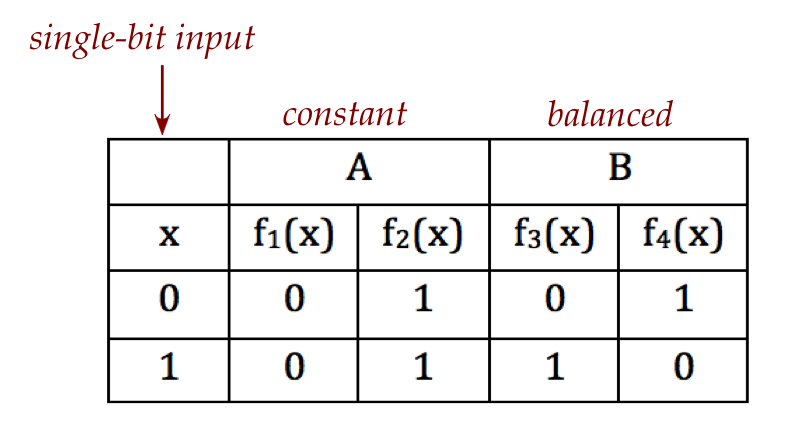
- The goal is to determine whether a mystery function
\(f\) is either in category A (that is, \(f_1\) or \(f_2\))
or in category B (\(f_3\) or \(f_4\)).
- Why have a goal like this?
- We know: two trials are needed for a classical solution.

- Could we use superposition with a single trial in the quantum case?

- In the quantum version,
we are given \(U_f\) where \(f\) is either in category A
(constant) or category B (balanced):
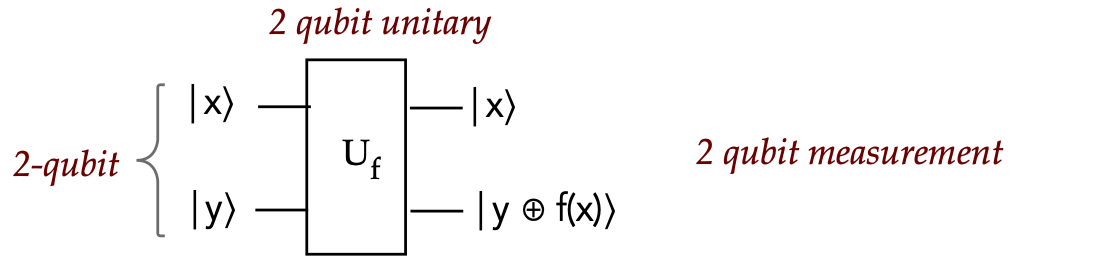
- By evaluating (supplying inputs), we want to determine
which category.
Let's try some example inputs:
In-Class Exercise 2:
- Complete the analysis for rows 2 and 4 of the table above.
- (Optional for undergrads)
Show why a 2-qubit Bell measurement cannot
distinguish \(f\in A\) vs \(f\in B\)
with a single trial. Work through the outcomes with projective
measurement and explain.
We'll now consider using a superposition in each of two qubits:
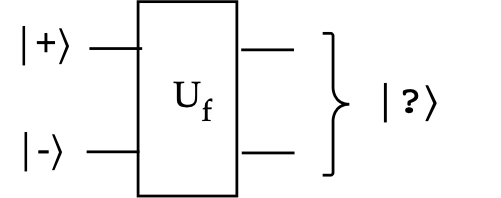
Before we analyze, let's recall a consequence of global vs. relative phase:
- Suppose \(x\) represents a single-bit Boolean value.
- Consider the (un-normalized) two-qubit state
$$
\kt{0} \otimes \kt{x} \plss \kt{1} \otimes (-\kt{x})
$$
Then
$$\eqb{
\kt{0} \otimes \kt{x} \plss \kt{1} \otimes (-\kt{x})
& \eql &
\kt{0} \otimes \kt{x} \plss \kt{1} \otimes (-1) \kt{x}
& \mbx{-1 is a constant} \\
& \eql &
\kt{0} \otimes \kt{x} \plss (-1) \parenl{\kt{1} \otimes \kt{x}}
& \mbx{Bilinearity} \\
& \eql &
\parenl{ \kt{0} + (-1) \kt{1}} \otimes \kt{x}
& \mbx{Tensor factoring} \\
& \eql &
\parenl{ \kt{0} - \kt{1}} \otimes \kt{x}
& \mbx{Simplification} \\
& \eql &
\sqrt{2} \kt{-} \otimes \kt{x}
& \mbx{Recall \(\kt{-}\)} \\
}$$
- On the other hand, consider the (un-normalized) state
$$
\kt{0} \otimes (-\kt{x}) \plss \kt{1} \otimes (-\kt{x})
$$
This simplifies as
$$\eqb{
\kt{0} \otimes (-\kt{x}) \plss \kt{1} \otimes (-\kt{x})
& \eql &
\kt{0} \otimes (-1) \kt{x} \plss \kt{1} \otimes (-1) \kt{x}
& \mbx{-1 is a constant} \\
& \eql &
(-1) \parenl{ \kt{0} \otimes \kt{x} \plss \kt{1} \otimes \kt{x} }
& \mbx{Bilinearity} \\
& \eql &
e^{i\pi} \parenl{ \kt{0} \otimes \kt{x} \plss \kt{1} \otimes \kt{x} }
& \mbx{Emphasizing phase} \\
& \eql &
\parenl{ \kt{0} \otimes \kt{x} \plss \kt{1} \otimes \kt{x} }
& \mbx{Global-phase equivalence} \\
& \eql &
\parenl{ \kt{0} + \kt{1} } \otimes \kt{x}
& \mbx{Tensor factoring} \\
& \eql &
\sqrt{2} \kt{+} \otimes \kt{x}
& \mbx{} \\
}$$
- Let's focus on the difference between the two starting
states:
$$\eqb{
\parenl{ \kt{0} \otimes \kt{x} } \plss \parenl{\kt{1} \otimes (-\kt{x})}
& \eql &
\parenl{ \kt{0} \otimes \kt{x} } \miss \parenl{\kt{1} \otimes \kt{x})}
& \mbx{Two terms have different sign} \\
\parenl{\kt{0} \otimes (-\kt{x})} \plss \parenl{\kt{1} \otimes (-\kt{x})}
& \eql &
\parenl{ \kt{0} \otimes \kt{x} } \plss \parenl{\kt{1} \otimes \kt{x})}
& \mbx{Two terms have same sign}
}$$
- The same-vs-different sign works the same when
$$\eqb{
\parenl{ \kt{0} \otimes (-\kt{x}) } \plss \parenl{\kt{1} \otimes \kt{x})}
& \eql &
(-1) \parenl{ \kt{0} \otimes \kt{x} \miss \kt{1} \otimes \kt{x})}
& \mbx{Two terms have different sign, global-phase -1} \\
\parenl{\kt{0} \otimes (\kt{x})} \plss \parenl{\kt{1} \otimes (\kt{x})}
& \eql &
\parenl{ \kt{0} \otimes \kt{x} } \plss \parenl{\kt{1} \otimes \kt{x})}
& \mbx{Two terms have same sign}
}$$
- In the first case we get \(\kt{-}\) as the first qubit, and in the
second, we get \(\kt{+}\).
- We will exploit this difference now.
We'll now apply \(\kt{+}\kt{-}\) as input to \(U_f\):

- First, we'll expand \(\kt{+}\kt{-}\) as
$$\eqb{
\kt{+}\kt{-} & \eql &
\isqt{1}\parenl{ \kt{0} + \kt{1} }
\,\otimes\, \isqt{1}\parenl{ \kt{0} - \kt{1} }\\
& \eql &
\frac{1}{2} \parenl{ \kt{0}\kt{0} - \kt{0}\kt{1} + \kt{1}\kt{0}
- \kt{1}\kt{1} }
}$$
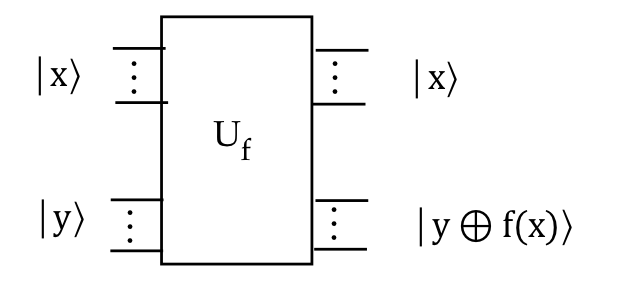
- Now
$$
U_f \kt{x}\kt{y} \eql \kt{x}\kt{y \oplus f(x)}
$$
for any \(U_f\).
- Thus,
$$\eqb{
U_f \kt{+}\kt{-}
& \eql &
U_f \frac{1}{2} \parenl{ \kt{0}\kt{0} \miss \kt{0}\kt{1} \plss \kt{1}\kt{0}
\miss \kt{1}\kt{1} }
& \mbx{Substituting the expanded form of \(\kt{+}\kt{-}\)}\\
& \eql &
\frac{1}{2} \parenl{
U_f \kt{0}\kt{0} \miss U_f \kt{0}\kt{1} \plss U_f \kt{1}\kt{0}
\miss U_f \kt{1}\kt{1} }
& \mbx{Linearity of \(U_f\)} \\
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0\oplus f(0)} \miss \kt{0}\kt{1\oplus f(0)} \plss
\kt{1}\kt{0\oplus f(1)} \miss \kt{1}\kt{1\oplus f(1)} }
& \mbx{Applying \(U_f\)} \\
}$$
- Consider the case when \(f=f_1: f(x) = 0\) for both \(x=0,x=1\):
- Then,
$$\eqb{
U_f \kt{+}\kt{-}
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0\oplus 0} \miss \kt{0}\kt{1\oplus 0} \plss
\kt{1}\kt{0\oplus 0} \miss \kt{1}\kt{1\oplus 0} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0} \miss \kt{0}\kt{1} \plss
\kt{1}\kt{0} \miss \kt{1}\kt{1} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0} (\kt{0} - \kt{1}) \plss
\kt{1} (\kt{0} - \kt{1}) } \\
& \eql &
\isqt{1} \parenl{
\kt{0} \kt{-} \plss
\kt{1} \kt{-} } \\
& \eql &
\isqt{1} \parenl{
\kt{0} + \kt{1} } \, \kt{-} \\
& \eql &
\kt{+}\kt{-} \\
}$$
- When \(f(x)=f_2(x) = 1\) for both \(x=0, x=1\) we get the
same result up to global phase:
$$
U_f \kt{+}\kt{-} \eql \kt{+}\kt{-}
$$
In-Class Exercise 3:
Show that this is true. That is,
\(U_{f_2} \kt{+}\kt{-} = \kt{+}\kt{-}\).
Next, consider \(f=f_3\):
- In this case, \(f_3(0)=0, f_3(1)=1\).
- Thus, with \(f=f_3\):
$$\eqb{
U_f \kt{+}\kt{-}
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0\oplus f(0)} \miss \kt{0}\kt{1\oplus f(0)} \plss
\kt{1}\kt{0\oplus f(1)} \miss \kt{1}\kt{1\oplus f(1)} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0\oplus 0} \miss \kt{0}\kt{1\oplus 0} \plss
\kt{1}\kt{0\oplus 1} \miss \kt{1}\kt{1\oplus 1} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0} \miss \kt{0}\kt{1} \plss
\kt{1}\kt{1} \miss \kt{1}\kt{0} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0}\kt{0} \miss \kt{0}\kt{1} \plss
(-1) \kt{1}\kt{0} \miss (-1) \kt{1}\kt{1} } \\
& \eql &
\frac{1}{2} \parenl{
\kt{0} \parenl{ \kt{0} - \kt{1} } \miss
\kt{1} \parenl{\kt{0} - \kt{1}} } \\
& \eql &
\isqt{1}\parenl{\kt{0} - \kt{1}} \isqt{1}\parenl{\kt{0} - \kt{1}} \\
& \eql &
\kt{-}\kt{-}
}$$
- Finally, when \(f=f_4\), we get the same output with
global phase:
$$
U_f \kt{+}\kt{-} \eql \kt{-}\kt{-}
$$
In-Class Exercise 4:
Show that this is true. That is,
\(U_{f_4} \kt{+}\kt{-} = \kt{-}\kt{-}\).
To summarize:
- When \(f \in A\) (i.e., \(f=\{f_1, f_2\}\))
$$
U_f \kt{+}\kt{-} \eql \kt{+}\kt{-}
$$
and when \(f\in B\) (i.e., \(f=\{f_3, f_4\}\))
$$
U_f \kt{+}\kt{-} \eql \kt{-}\kt{-}
$$
- Thus if we measure the first qubit in H-basis,
any \(f \in A\) will always result in \(\kt{+}\) output.
- And any \(f\in B\) will always result in \(\kt{-}\) output.
- And, so with a single input and measurement, we can
solve the problem.
- This demonstrates, for at least this oracle problem, that
a quantum approach is demonstrably faster than classical.
- We can describe this visually as:
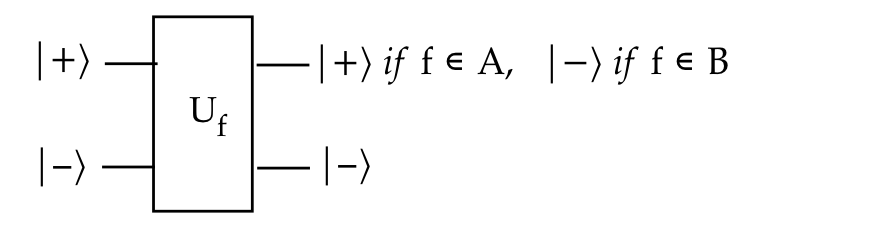
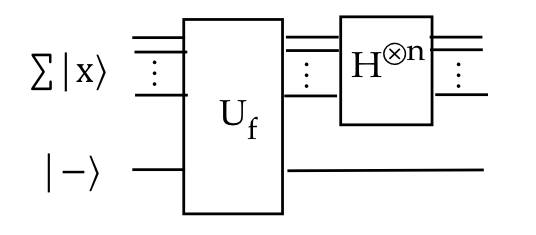
- Or fleshed out with measurement:
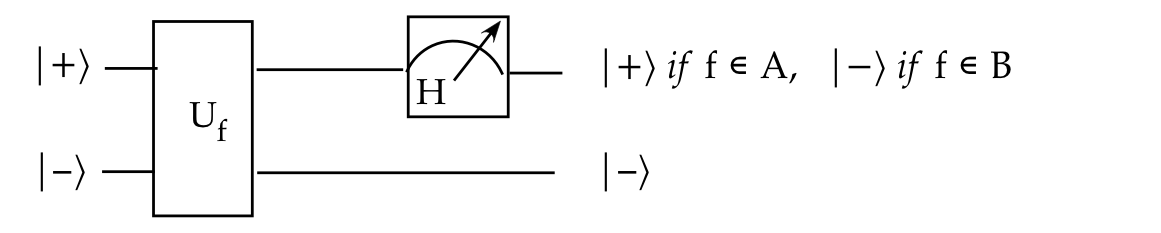
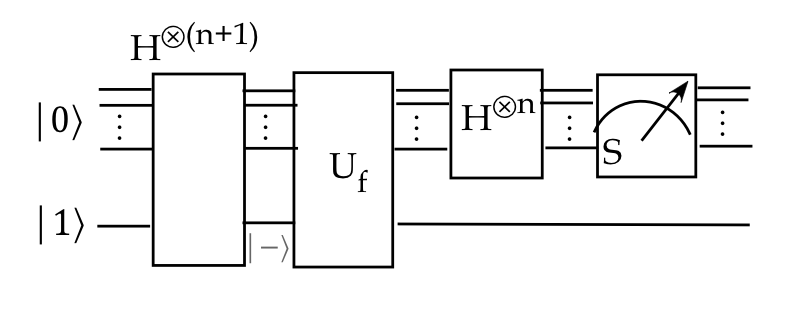
- And using standard gates:
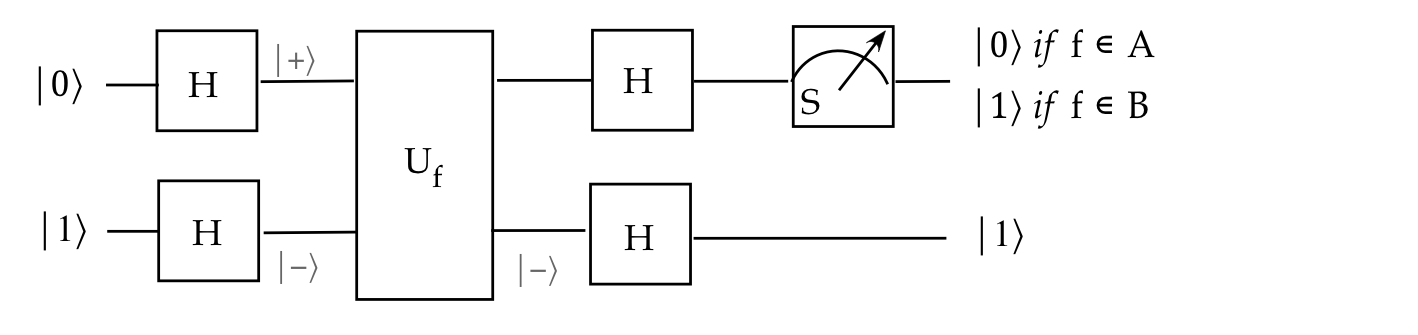
The doubling of speed for the single-bit problem above is not impressive.
However, the same idea can be extended to demonstrate
exponential speed up.
But before getting to those examples, we'll need a few
useful results.
9.3
Some useful results
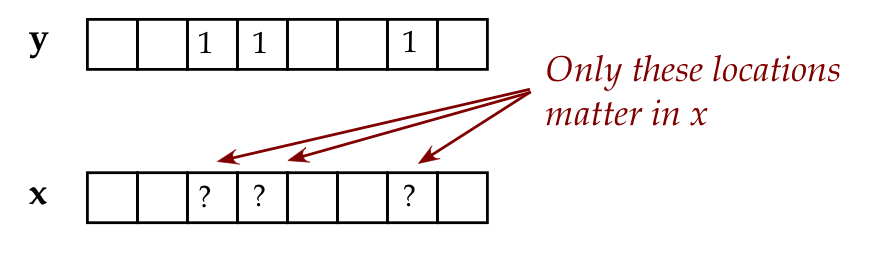
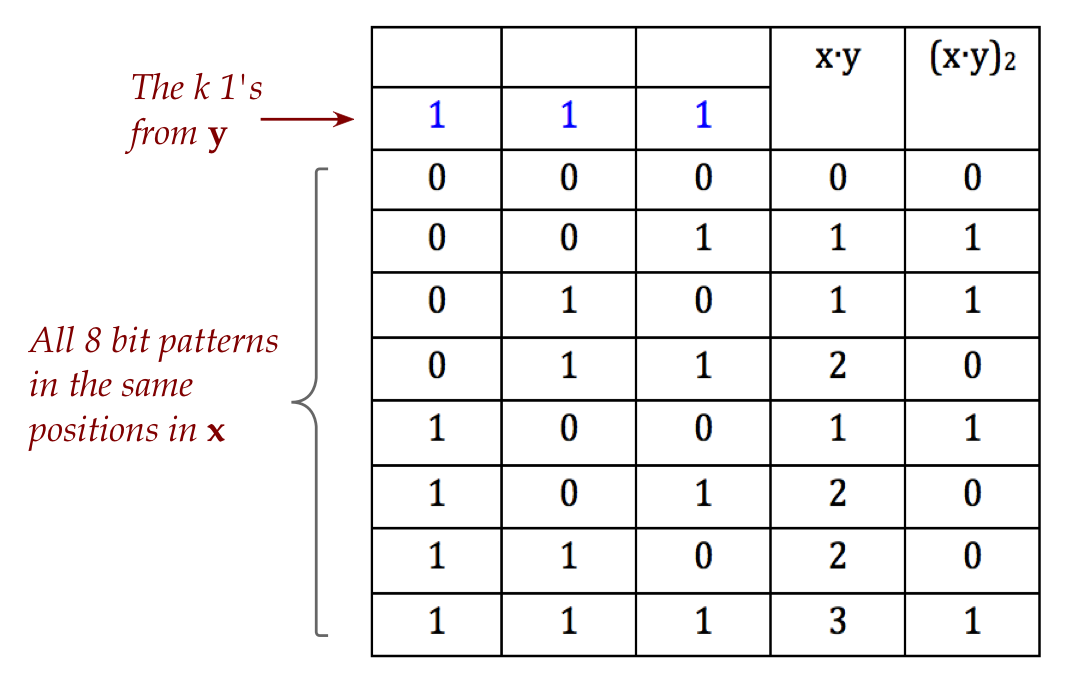
First, a result about the dot product of classical binary-vectors:
Next, let's review tensored Hadamards:
- Recall:
$$\eqb{
H \kt{0} & \eql & \kt{+} & \eql & \isqt{1} \parenl{\kt{0} + \kt{1}} \\
H \kt{1} & \eql & \kt{-} & \eql & \isqt{1} \parenl{\kt{0} - \kt{1}} \\
}$$
- We can write this as
$$
H \kt{x} \eql \isqt{1} \parenl{ \kt{0} + (-1)^x \kt{1} }
$$
where \(x\) is the binary variable \(x\in \{0,1\}\).
- We'll take this a step further by introducing
a second variable \(y\):
$$\eqb{
H \kt{x} & \eql & \isqt{1} \parenl{ \kt{0} + (-1)^x \kt{1} } \\
& \eql &
\isqt{1} \parenl{ (-1)^0\kt{y=0} \, + \, (-1)^x \kt{y=1} } \\
& \eql &
\isqt{1} \parenl{ (-1)^{0\cdot y} \kt{y=0} \, + \, (-1)^{x\cdot y} \kt{y=1} } \\
& \eql &
\isqt{1} \sum_{y=0}^1 (-1)^{xy} \kt{y}
}$$
- Now recall that \( H^{\otimes n} \) applied
to \(\kt{00\ldots 0}\) produces the equal superposition:
$$
H^{\otimes n} \kt{00\ldots 0}
\eql
\frac{1}{\sqrt{N}} \sum_{y}^{N-1} \kt{y}
$$
where \(N=2^n\) and \(y\) is in decimal form:
$$
\kt{y} \in \setl{ \kt{0}, \kt{1}, \kt{2}, \ldots, \kt{N-1} }
$$
- We'll use our new notation to derive this easily:
$$\eqb{
H^{\otimes n} \kt{00\ldots 0}
& \eql &
\parenl{H \otimes H \otimes \ldots \otimes H} \kt{0} \kt{0}
\ldots \kt{0} \\
& \eql &
H\kt{0} \otimes H\kt{0} \otimes \ldots \otimes H \kt{0} \\
& \eql &
\parenl{\isqt{1} \sum_{y_{n-1}=0}^1 \kt{y_{n-1}} }
\otimes
\parenl{\isqt{1} \sum_{y_{n-2}=0}^1 \kt{y_{n-2}} }
\otimes
\ldots
\otimes
\parenl{\isqt{1} \sum_{y_{0}=0}^1 \kt{y_{0}} } \\
& \eql &
\frac{1}{\sqrt{N}}
\sum_{y_{n-1},\ldots,y_0}
\kt{y_{n-1}} \kt{y_{n-2}} \ldots \kt{y_{0}} \\
& \eql &
\frac{1}{\sqrt{N}}
\sum_{y=0}^{N-1}
\kt{y}
}$$
where we switched to decimal notation in the last step.
- Note: we have applied \( H^{\otimes n} \)
to the standard-basis vector \(\kt{00\ldots 0}\).
- We are going to need to see what we get when
\( H^{\otimes n} \) is applied to any other standard basis vector.
- Conveniently, it has a compact form:
Proposition 9.2:
$$
H^{\otimes n} \kt{x}
\eql
\frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} (-1)^{ {x}\cdot{y} } \kt{y}
$$
Proof:
$$\eqb{
H^{\otimes n} \kt{x}
& \eql &
\parenl{H \otimes H \otimes \ldots \otimes H} \kt{x_{n-1}} \kt{x_{n-1}}
\ldots \kt{x_0} \\
& \eql &
H\kt{x_{n-1}} \otimes \kt{x_{n-1}} \otimes \ldots \otimes
H\kt{x_0} \\
& \eql &
\parenl{\isqt{1} \sum_{y_{n-1}=0}^1 (-1)^{x_{n-1}y_{n-1}} \kt{y_{n-1}} }
\otimes
\parenl{\isqt{1} \sum_{y_{n-2}=0}^1 (-1)^{x_{n-2}y_{n-2}} \kt{y_{n-2}} }
\otimes
\ldots
\otimes
\parenl{\isqt{1} \sum_{y_{0}=0}^1 (-1)^{x_{0}y_{0}}\kt{y_{0}} } \\
& \eql &
\frac{1}{\sqrt{N}}
\sum_{y_{n-1},\ldots,y_0}
(-1)^{x_{n-1}y_{n-1}} (-1)^{x_{n-2}y_{n-2}} \ldots (-1)^{x_{0}y_{0}}
\kt{y_{n-1}} \kt{y_{n-2}} \ldots \kt{y_{0}} \\
& \eql &
\frac{1}{\sqrt{N}}
\sum_{y=0}^{N-1}
(-1)^{x_{n-1}y_{n-1} + x_{n-2}y_{n-2} \ldots x_{0}y_{0}}
\kt{y} \\
& \eql &
\frac{1}{\sqrt{N}}
\sum_{y=0}^{N-1}
(-1)^{ {x}\cdot{y} }
\kt{y}
}$$
- Compare \(H^{\otimes n} \kt{0}\) with \(H^{\otimes n} \kt{x}\):
(\(\kt{x}\) is a standard basis vector.)
$$
H^{\otimes n} \kt{x} \eql \frac{1}{\sqrt{N}}
\sum_{y=0}^{N-1}
\kt{y}
\;\;\;\;\;\;\;\;
H^{\otimes n} \kt{x} \eql \frac{1}{\sqrt{N}}
\sum_{y=0}^{N-1}
(-1)^{ {x}\cdot{y} }
\kt{y}
$$
- We see that \(H^{\otimes n} \kt{x}\) also produces a superposition
of standard-basis vectors, except that some of them have negative signs.
- The signs are determined by \(x\cdot y\).
9.4
The Deutsch-Jozsa algorithm
Let's first state the problem:
- Let \(S_n = 2^{\{0,1\}} = \mbox{all n-bit binary patterns}\).
- Here, we consider Boolean functions \(f: S_n \to \{0,1\}\).
- That is, n-bit input, and 1-bit output.
- A function \(f\) is constant if either:
- \(f(x) = 0\) for all \(x\)
- \(f(x) = 1\) for all \(x\)
- A function \(f\) is balanced if
\(f(x)=0\) for exactly half the inputs \(x\in S_n\). That is,
$$
\mag{\setl{x: f(x)=0}} \eql \frac{2^{n}}{2}
$$
- For example (\(n=3\)):
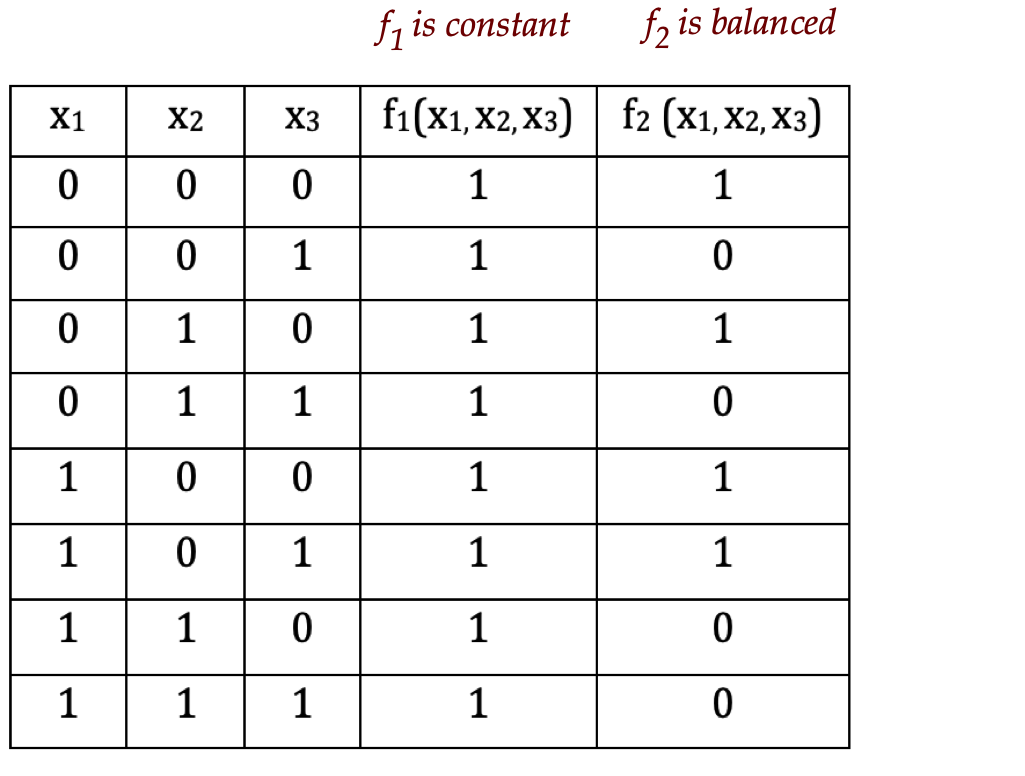
- The objective of the problem:
- We are given that \(f\) is either constant or balanced.
- How many trials (different evaluations with inputs) does it
take to distinguish whether constant or balanced?
- The classical solution will, in the worst-case, need
to evaluate just over half the inputs
\(\rhd\)
\(2^{n-1} + 1\) trials
- We will show that a single trial is sufficient for a
quantum algorithm.
\(\rhd\)
An exponential speed up.
To begin, let's take a closer look at the output qubit
in our customary set up:
- First, we'll use the symmetry of XOR to write
\(\kt{f(x) \oplus y}\):
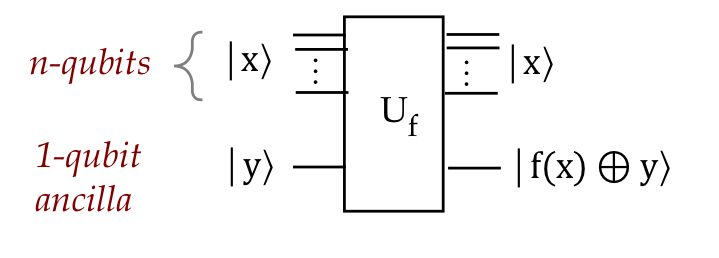
Here, \(y \in \{0,1\}\) is a single bit.
- Notice:
- When \(f(x)=0\), the output is just \(y\).
- When \(f(x)=1\), the output is \(y^\prime\).
\(\rhd\)
That is, \(f(x)=1\) "flips" \(y\).
- We can think of this as applying the \(X\) gate to
\(\kt{y}\) whenever it is controlled by \(f(x)\).
- Now let's ask: what if \(\kt{y}\) were any qubit state?
- Let \(\kt{y} = \alpha\kt{0} + \beta\kt{1}\).
- Consider \(f(x)=0\). Then,
$$\eqb{
U_f \kt{x}\kt{y}
& \eql &
U_f \kt{x} \parenl{ \alpha\kt{0} + \beta\kt{1} } \\
& \eql &
\alpha U_f \kt{x} \kt{0} \, + \, \beta U_f \kt{x}\kt{1} \\
& \eql &
\alpha \kt{x} \kt{f(x) \oplus 0} \, + \, \beta \kt{x}\kt{f(x) \oplus 1} \\
& \eql &
\alpha \kt{x} \kt{0 \oplus 0} \, + \, \beta \kt{x}\kt{0 \oplus 1} \\
& \eql &
\alpha \kt{x} \kt{0} \, + \, \beta \kt{x}\kt{1} \\
& \eql &
\kt{x} \parenl{ \alpha \kt{0} + \beta \kt{1} } \\
& \eql &
\kt{x} \kt{y}\\
}$$
- And when \(f(x)=1\)
$$\eqb{
U_f \kt{x}\kt{y}
& \eql &
\alpha \kt{x} \kt{f(x) \oplus 0} \, + \, \beta \kt{x}\kt{f(x) \oplus 1} \\
& \eql &
\alpha \kt{x} \kt{1 \oplus 0} \, + \, \beta \kt{x}\kt{1 \oplus 1} \\
& \eql &
\alpha \kt{x} \kt{1} \, + \, \beta \kt{x}\kt{0} \\
& \eql &
\kt{x} \parenl{ \alpha \kt{1} + \beta \kt{0} } \\
& \eql &
\kt{x} \parenl{ X\kt{y} }
}$$
- Thus, it does work for arbitrary \(\kt{y}\).
- Now consider the special case \(\kt{y} = \kt{-}\):
- When \(f(x)=0\):
$$
U_f \kt{x}\kt{-} \eql \kt{x}\kt{-}
$$
- When \(f(x)=1\):
$$
U_f \kt{x}\kt{-} \eql \kt{x}X \kt{-} \eql \kt{x} (-1) \kt{-}
$$
because \(X\kt{-} = -\kt{-}\).
- We can summarize this as:
$$
U_f \kt{x}\kt{-} \eql (-1)^{f(x)} \kt{x} \kt{-}
$$
- Now we can see what \(U_f\) does to the equal superposition:
Proposition 9.3:
$$
U_f \frac{1}{\sqrt{N}} \sum_{x} \kt{x}\kt{-}
\eql \frac{1}{\sqrt{N}} \sum_x (-1)^{f(x)} \kt{x} \kt{-}
$$
Proof:
Simple application of the linearity of \(U_f\).
Now to the algorithm:
What do we learn from this example?
- We already know that \(H^{\otimes n}\) is useful in
producing the equal n-qubit superposition.
- But we now see that \(H^{\otimes n}\) can be useful
in the middle of a circuit as well.
- Using \(\kt{-}\) as an ancilla value results in getting
signs \( (-1)^{f(x)} \) entangled with different states in
the superposition:
- Then, by analyzing how the signs for a pattern, we
saw how one state's amplitude was boosted.
- We got lucky that the boost was maximal (probability = 1).
- Even if not maximal, we could repeat the entire process
so that a high-probability informative state is measured as outcome.
- One new trick learned:
- We don't need to fully analyze a complicated expression.
- Just knowing that a key state's amplitude was boosted might be enough.
- We also need to acknowledge: this is a highly artificial
problem, almost designed in reverse.
9.5
The Bernstein-Vazirani algorithm
First, the problem:
- In the following, we'll assume the dot-operator
applies with mod-2:
$$
(c\cdot x)_2 \eql \parenl{ \sum_i c_i x_i } \mbox{ mod } 2
$$
An alternate notation is:
$$
(c\cdot x)_2 \; =_2 \; c\cdot x
$$
- Let \(f(x) = (c\cdot x)_2\) be a Boolean function where
both \(c\) and \(x\) are binary strings or vectors.
- We are given a blackbox that implements \(f(x)\) but not
told what \(c\) is.
- The goal is to find \(c\) using a minimum number of queries.
- Note: the output \(f(x)\) is a single bit (\(0\) or \(1\)).
- For example, suppose \(c=101\)
- When using \(x=100\), we see that \(f(x) = (101)\cdot (100) = 1\),
from which we conclude the first bit of \(c\) is \(1\).
- Then, using \(x=010\), the second bit is \(0\).
- And, using \(x=001\), the third bit \(1\).
- Note: using \(x=111\) is not useful because
\(f(x) = (101)\cdot (111) = 0\)
\(\rhd\)
We can't conclude anything definitive.
- Thus, the classical approach requires \(n\) queries.
- We'll now see that a quantum algorithm can return \(c\)
in a single query.
The algorithm:
- The machinery of Deutsch-Jozsa can be used to solve this
problem using \(f(x)= (c\cdot x)_2\).
- We start the same way with
$$
\ksi \eql U_f \frac{1}{\sqrt{N}} \sum_{x} \kt{x}\kt{-}
\eql \frac{1}{\sqrt{N}} \sum_x (-1)^{f(x)} \kt{x} \kt{-}
$$
and apply \(H^{\otimes n} \otimes I\) to get
$$
(H^{\otimes n} \otimes I) \ksi
\frac{1}{N}
\sum_{x,y} (-1)^{f(x)} (-1)^{ ({x}\cdot{y})_2 } \kt{y}\kt{-}
$$
- At this point, we substitute for the new \(f(x)\) in this problem:
$$
(H^{\otimes n} \otimes I) \ksi
\frac{1}{N}
\sum_{x,y} (-1)^{ (c\cdot x)_2} (-1)^{ ({x}\cdot{y})_2 } \kt{y}\kt{-}
$$
- In Deutsch-Jozsa, we separated out the term with
\(\kt{0}\kt{-}\).
- Here, we'll examine the term \(\kt{c}\kt{-}\).
\(\rhd\)
That is, when \(y=c\).
- The coefficient of \(\kt{c}\kt{-}\) turns out to be \(1\):
$$\eqb{
\frac{1}{N}
\sum_{x} (-1)^{ (c\cdot x)_2} (-1)^{ (c\cdot x)_2} \kt{c}\kt{-}
& \eql &
\parenl{ \frac{1}{N} \sum_{x} (-1)^{ (c\cdot x)_2} (-1)^{ (c\cdot x)_2} }
\kt{c}\kt{-} \\
& \eql &
\parenl{ \frac{1}{N} \sum_{x} (1) }
\kt{c}\kt{-} \\
& \eql &
\parenl{ \frac{1}{N} N }
\kt{c}\kt{-} \\
& \eql &
\kt{c}\kt{-}
}$$
That is, happily, \(\kt{c}\) is the only outcome possible.
- Thus, the same circuit as in Deutsch-Jozsa with the new \(f\)
directly produces \(c\) as its only outcome from a single measurement.
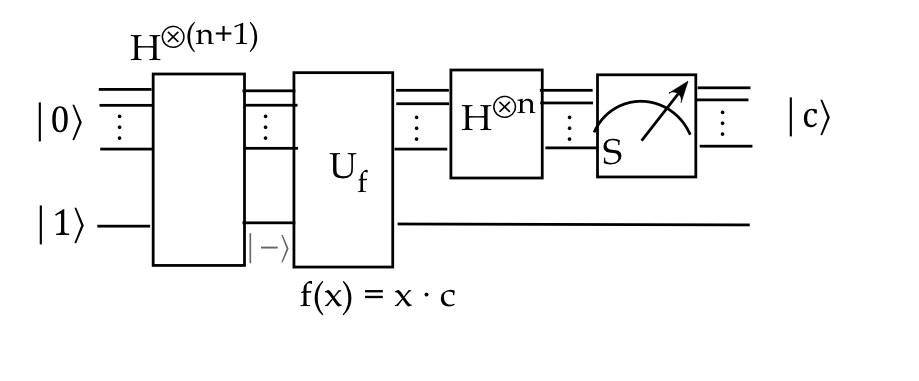
9.6
Simon's algorithm
First, two tiny useful results:
- Proposition 9.4:
For binary vectors \(x,y,c\):
- \(x \oplus y = y \oplus x\)
- \(x \oplus (c \oplus y) = (x \oplus c) \oplus y\)
- If \(x \oplus c = y\) then:
- \(y \oplus c = x\)
- \(x \oplus y = c\)
Proof:
The commutativity and associativity follow from examining each bit.
Clearly, \(x_i \oplus y_i = y_i \oplus x_i\)
For associativity, we can write out the truth-table:
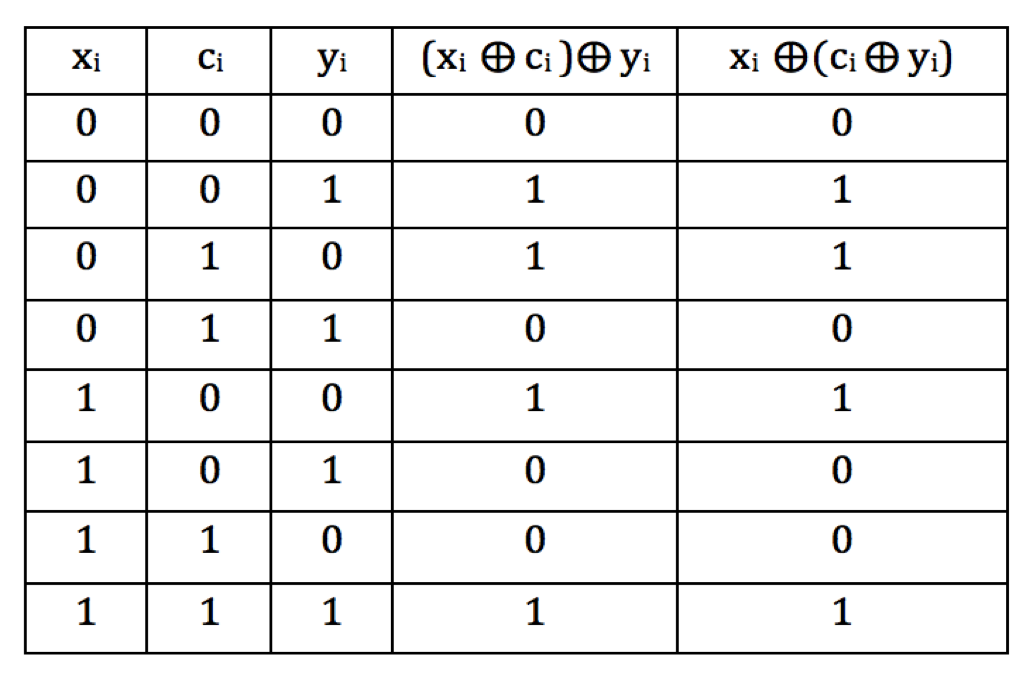
Because no bit affects any other, the result holds for the vectors.
From
$$
y \eql x \oplus c
$$
we get
$$
y \oplus c \eql (x \oplus c) \oplus c \eql x \oplus (c \oplus
c) \eql x
$$
or
$$
y \oplus c \eql x
$$
Left-XORing this with \(y\) gives us the second result.
- Proposition 9.5:
For binary vectors \(x,y,c\):
$$
(x \oplus c) \cdot y \; =_2 \; x\cdot y + c\cdot y
$$
Proof:
The proof follows by working out the truth table for single bits:
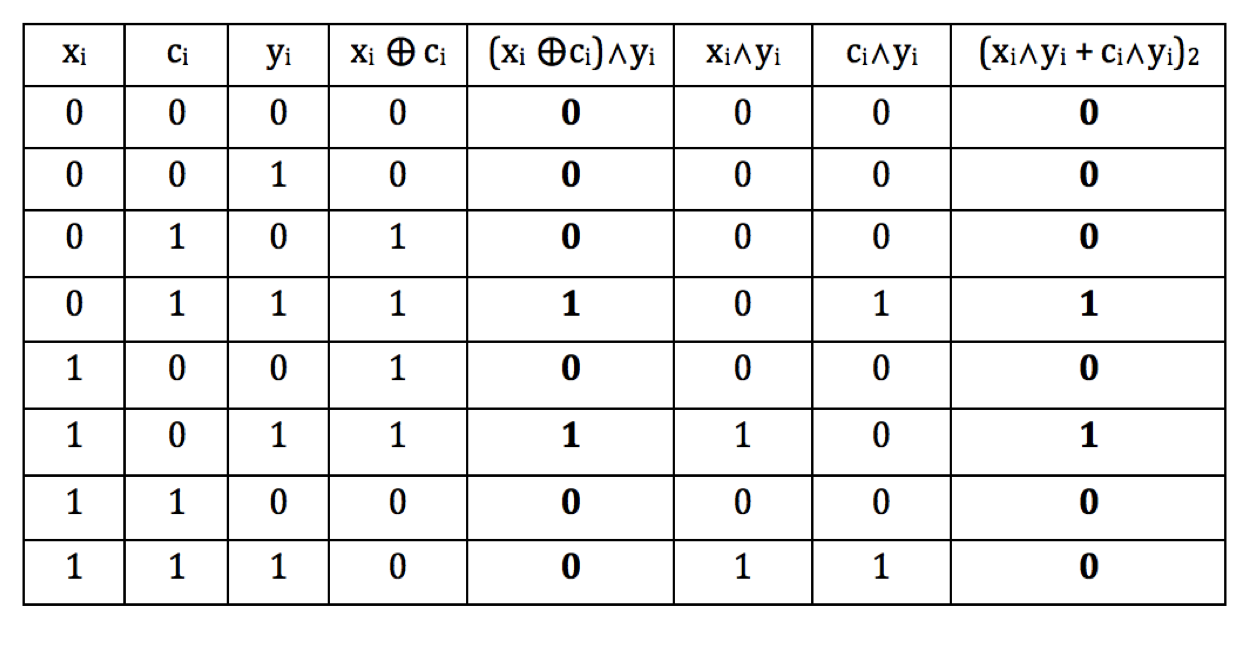
Now let's describe the problem to be solved:
- We are given a function \(f:S_n \to S_n\), that is,
from n-bit strings to n-bit strings.
- The function \(f\) has the following two properties:
- \(f\) is 2-to-1: for any \(x\), there is exactly one \(y\)
such that \(f(x)=f(y)\).
- There is an unknown vector \(c\) such that
\(f(x \oplus c) = f(x)\) for all \(x\).
\(\rhd\)
The goal: find \(c\)
- Thus, when \(f(x)=f(y)\), we are given that \(y = c \oplus x\).
- Here's a 3-bit example with \(c=110\):
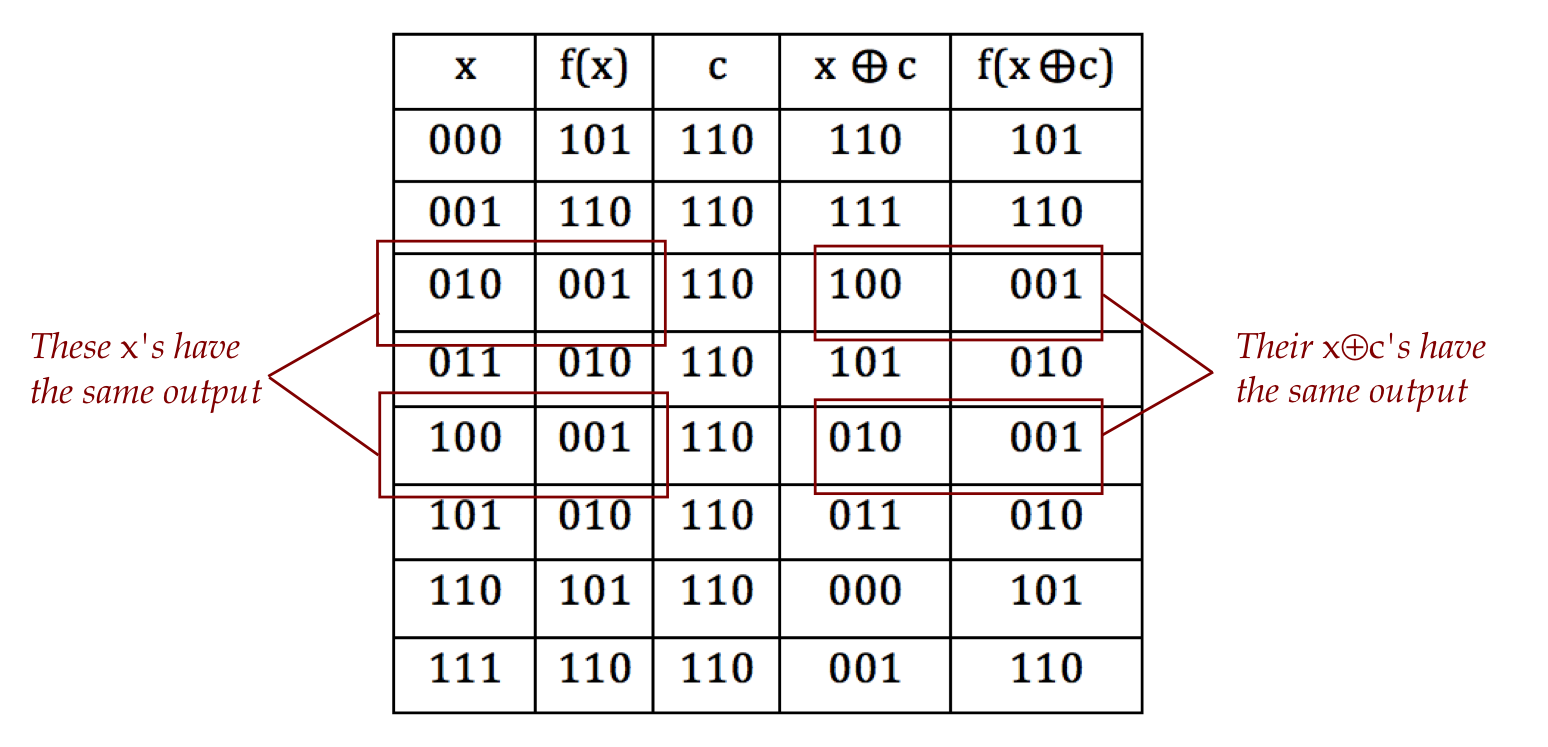
- The number \(c\) is something like a period:
- For a real function \(f(x)\), if \(f(x+T) = f(x)\), then
\(T\) is called the period.
- Because the condition \(f(x \oplus c) = f(x)\) is similar,
\(c\) is called the period in this case.
- Note: there is no equivalent notion of distance in this binary case.
- The goal of the problem: discover the period \(c\) with
as few queries (function evaluations) as possible.
- How long does the best classical algorithm need?
- Such an algorithm needs to try \(x\) and \(y\) until
the first such pair gives \(f(x) = f(y)\).
- At this time, we know \(x \oplus c = y\).
- From Proposition 9.4, we know then that \(c = x \oplus y\).
- What is the best one can do in trying different \(x\)?
- Suppose we start at \(x=0\), and try every \(x\) in sequence:
\(x=1, x=2, \ldots\).
(That is, try row-by-row in the truth table)
- Then we are guaranteed to find at least one repeat \(f(x)\).
\(\rhd\)
\(2^{n-1} + 1\) evaluations worst-case
Simon's algorithm:
- The starting point is the full-superposition and
an \(n\)-qubit ancilla of \(\kt{00\ldots 0}\):
$$
\ksi \eql \frac{1}{\sqrt{N}} \sum_x \kt{x}\kt{0}
$$
- Now apply \(U_f\):
$$\eqb{
U_f \ksi & \eql & \frac{1}{\sqrt{N}} \sum_x U_f \kt{x}\kt{0} \\
& \eql & \frac{1}{\sqrt{N}} \sum_x \kt{x}\kt{0 \oplus f(x)} \\
& \eql & \frac{1}{\sqrt{N}} \sum_x \kt{x}\kt{f(x)} \\
}$$
- Note: because \(f:S_n\to S_n\), the vector
\(\kt{f(x)}\) is an \(n\)-qubit vector.
- Next, we measure this set of qubits (the second \(n\) qubits) in
the S-basis.
- Which means the outcome vector will be \(\kt{f(x^\prime)}\)
for some input bit pattern \(x^\prime\).
- Now because there are two inputs that result in this output
value, there is some \(y^\prime\) such that
$$
\kt{f(y^\prime)} \eql \kt{f(x^\prime)}
$$
where
$$
y^\prime \eql x^\prime \oplus c
$$
- Examine now the original \(2n\)-qubit output before measurement:
$$
U_f \ksi
\eql \frac{1}{\sqrt{N}} \sum_x \kt{x}\kt{f(x)} \\
$$
- Because \(\kt{x}\kt{f(x)}\) are entangled, if
measurement shows \(\kt{f(x^\prime)}\), then the top \(n\)-qubits
will have some combination of \(\kt{x^\prime}\) or \(\kt{y^\prime}\).
- That is, the outcome will be a linear combination
$$
\mbox{(constant)} \kt{x^\prime}\kt{f(x^\prime)}
\plss
\mbox{(constant)} \kt{y^\prime}\kt{f(y^\prime)}
$$
- But all the inputs are in equal superposition, so the outcome
is in fact:
$$
\isqt{1} \kt{x^\prime}\kt{f(x^\prime)} \plss
\isqt{1} \kt{y^\prime}\kt{f(y^\prime)}
$$
- Which simplifies to:
$$
\isqt{1} \parenl{ \kt{x^\prime} + \kt{y^\prime} } \kt{f(x^\prime)}
$$
(Since \(f(x^\prime)=f(y^\prime)\))
- Finally, substitute \(y^\prime = x^\prime \oplus c\) to get:
$$
\isqt{1} \parenl{ \kt{x^\prime} + \kt{x^\prime \oplus c} } \kt{f(x^\prime)}
$$
- Let's call this \(\kt{\psi_2}\):
$$
\kt{\psi_2} \eql \isqt{1} \parenl{ \kt{x^\prime} +
\kt{x^\prime \oplus c} } \kt{f(x^\prime)}
$$
- Recall the mod-2 variation of Proposition 9.2:
$$
H^{\otimes n} \kt{x}
\eql
\frac{1}{\sqrt{N}} \sum_{y}^{N-1} (-1)^{ ({x}\cdot{y})_2 } \kt{y}
$$
- We now apply \(H^{\otimes n}\) to the top \(n\) qubits:
$$\eqb{
(H^{\otimes n} \otimes I_n) \kt{\psi_2}
& \eql &
(H^{\otimes n} \otimes I_n)
\isqt{1} \parenl{ \kt{x^\prime} + \kt{x^\prime \oplus c} }
\kt{f(x^\prime)} \\
& \eql &
\isqt{1} (H^{\otimes n} \otimes I_n)
\kt{x^\prime} \kt{f(x^\prime)}
\; + \; \isqt{1} (H^{\otimes n} \otimes I_n)
\kt{x^\prime \oplus c} \kt{f(x^\prime)} \\
& \eql &
\isqt{1} \frac{1}{\sqrt{N}} \sum_y
(-1)^{ (x^\prime \cdot y)_2} \kt{f(x^\prime)}
\; + \;
\isqt{1} \frac{1}{\sqrt{N}} \sum_y
(-1)^{ ((x^\prime \oplus c )\cdot y)_2} \kt{f(x^\prime)} \\
& \eql &
\isqt{1} \frac{1}{\sqrt{N}}
\sum_y \left( (-1)^{ (x^\prime \cdot y)_2} + (-1)^{ ((x^\prime
\oplus c )\cdot y)_2} \right)
\kt{y} \kt{f(x^\prime)} \\
& \eql &
\isqt{1} \frac{1}{\sqrt{N}}
\sum_y \left( (-1)^{ (x^\prime \cdot y)_2}
+ (-1)^{ (x^\prime \cdot y)_2} (-1)^{(c \cdot y)_2}
\right)
\kt{y} \kt{f(x^\prime)} \\
& \eql &
\isqt{1} \frac{1}{\sqrt{N}}
\sum_y \left( (-1)^{ (x^\prime \cdot y)_2} \left[ 1
+ (-1)^{(c \cdot y)_2} \right]
\right)
\kt{y} \kt{f(x^\prime)} \\
}$$
Note: in going to the last step, we applied Proposition 9.5, where
for binary vectors \(x,y,c\):
$$
(x \oplus c) \cdot y \; =_2 \; x\cdot y + c\cdot y
$$
- Now,
$$
\left[1 + (-1)^{(c \cdot y)_2} \right]
\eql
\left\{
\begin{array}{cc}
2 & \mbox{if \(c \cdot y =_2 0\)} \\
0 & \mbox{if \(c \cdot y =_2 1\)} \\
\end{array}
\right.
$$
- Thus, any measurement of the top \(n\) qubits, will produce as
outcome some \(\kt{y}\) such \(c\cdot y =_2 0\).
- Suppose we perform this entire sequence once and obtain
some \(\kt{y_1}\) as outcome.
\(\rhd\)
Then \(c\cdot y_1 =_2 0\).
- Now we repeat and get some \(\kt{y_2}\) as outcome.
\(\rhd\)
Then \(c\cdot y_2 =_2 0\).
- All we need are n linearly independent equations
$$\eqb{
c \cdot y_1 & \; =_2 \; & 0 \\
c \cdot y_2 & \; =_2 \; & 0 \\
& \vdots & \\
c \cdot y_n & \; =_2 \; & 0 \\
}$$
Each time an outcome is produced, we classically check
that it is linearly independent of the previous ones.
- It turns out, one can show, that with very high probability
\(O(n)\) trials will result in a linearly independent set of equations.
- These can be solved for \(c\).
- The solution procedure is similar to regular linear equations.
- A pivot is identified for each column.
- Zeroes in the column in other rows are produced by XOR-ing rows.
- The linear-independence and solution can be combined into
a single procedure that keeps the current set in RREF form,
and adds a new equation to test independence.
- To summarize:
- The circuit can be described as:
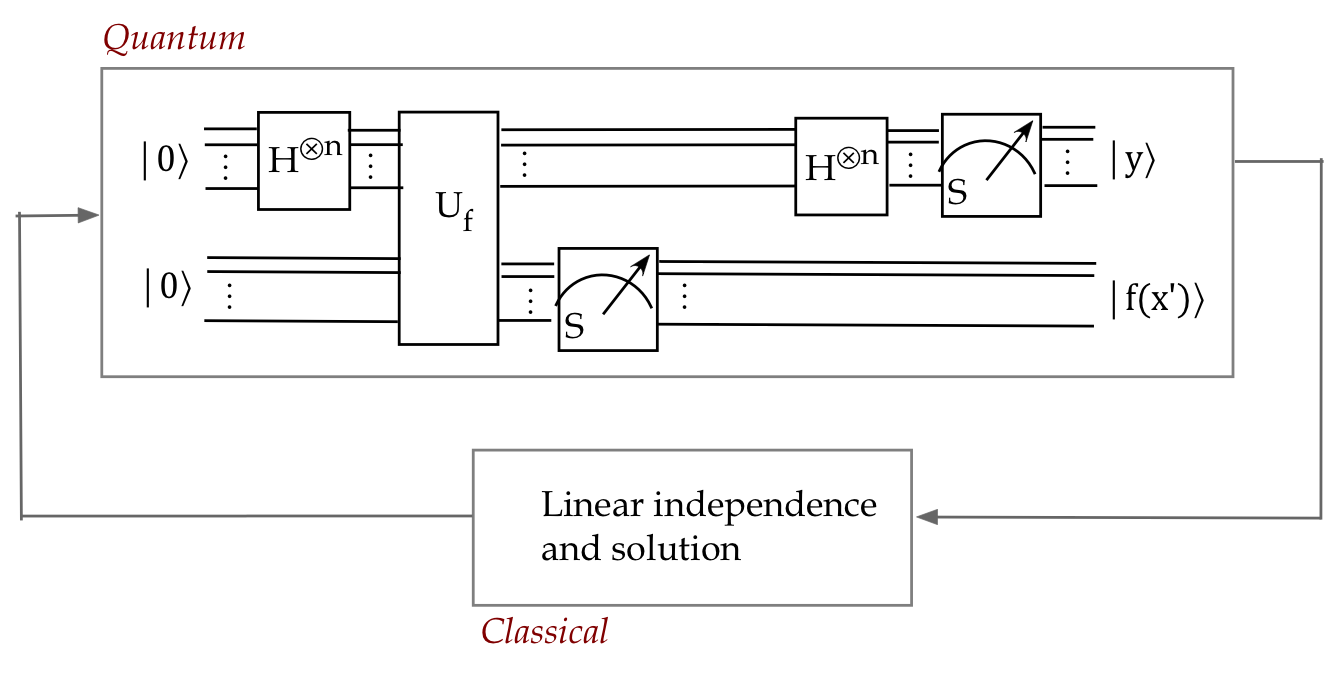
- Trials are repeated until \(n\) independent equations
\(c\cdot y_i =_2 0\) are found.
- The equations are classically solved for \(c\).
- With very high probability, only \(O(n)\) trials
are needed, in comparison to an exponential classical solution.
What do we learn from this problem and algorithm?
- This algorithm exemplifies how a combination of
quantum-and-classical can iteratively solve a problem.
- It's not necessary for a quantum algorithm to solve
a problem in one-shot.
- The output can be probabilisitic, as long as
desired outcomes occur with high enough probability.
- We learned an important small trick that will be useful
in other algorithms:
- We can measure part of the output to force a
superposition in the other part.
- For example, consider
$$
\ksi \eql \kt{a}\kt{0} + \kt{b}\kt{0} + \kt{c}\kt{1} + \kt{d}\kt{1}
$$
If we measure the second qubit and obtain \(\kt{0}\), we know
the 2-qubit outcome is:
$$
\kt{a}\kt{0} + \kt{b}\kt{0} \eql (\kt{a} + \kt{b})\kt{0}
$$
Which places the first qubit outcome in a superposition.
- Such superpositions can then be used to further simplify
(as above) or be further modified (Shor's algorithm).
- The problem is no less contrived than the other oracle problems.
- However, this problem provided insight that led
to Shor's algorithm.
9.7
Summary
What have we learned so far?
- A set of highly artifical problems can be solved faster
with a quantum algorithm:
- (Single-qubit) Deutsch's Algorithm is twice as fast as classical.
- A classical algorithm needs to apply \(f(x)\) twice
- Deutsch's Algorithms applies \(U_f\) once
- (Multiple-qubits) Deutsch-Jozsa, Bernstein-Vazirani and Simon's
algorithms are all exponentially faster than classical.
- A classical algorithm needs \(2^{n-1} + 1\) function evaluations
- The quantum algorithm needs a single evaluation
- The algorithms use "quantum tricks" to achieve their speedup:
- (All four algorithms) Supply superposition inputs using \(H^{\otimes n} \kt{0}\)
- Apply \(H^{\otimes n}\) for other purposes as well, for example,
in Bernstein-Vazirani:
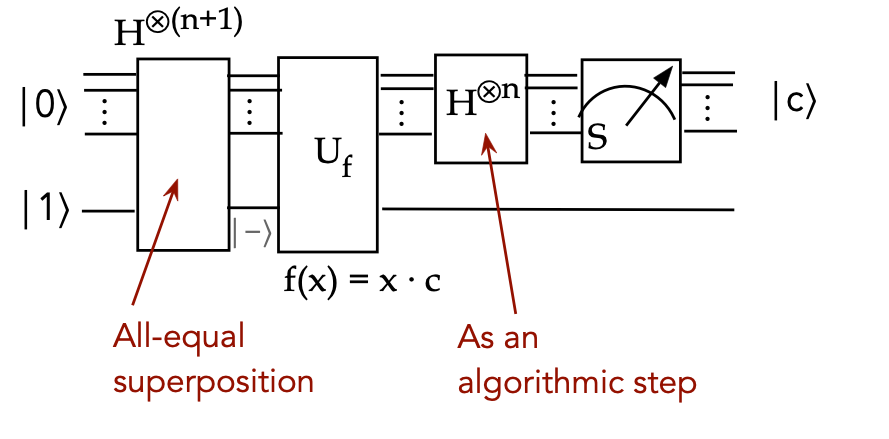
- Measure a subset of qubits and then apply other operators,
for example, in Simon's:
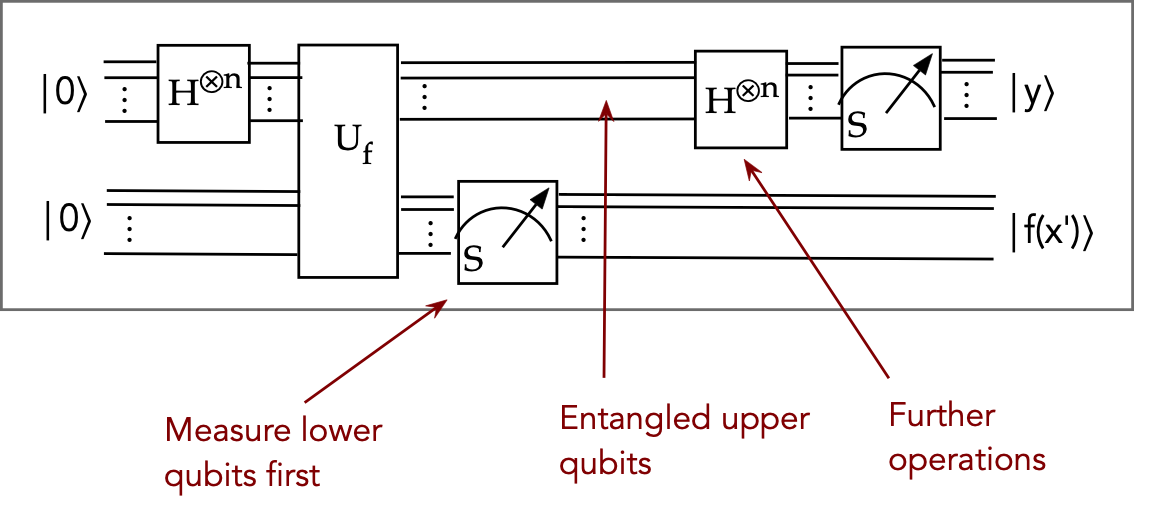
- Repeat the whole computation to get a series of classical outputs
(Simon's)
- Analysis also used some new tricks:
- A convenient expression for \(H^{\otimes n} \kt{x}\) (Proposition 9.2):
$$
H^{\otimes n} \kt{x}
\eql
\frac{1}{\sqrt{N}} \sum_{y=0}^{N-1} (-1)^{ {x}\cdot{y} } \kt{y}
$$
- Separating out particular vectors for their coefficients
- Could these tricks become building blocks for future
quantum algorithms?
There is something we have not addressed:
- What is the circuit for \(U_f\)?
- For example, consider the Deutsch-Jozsa algorithm:
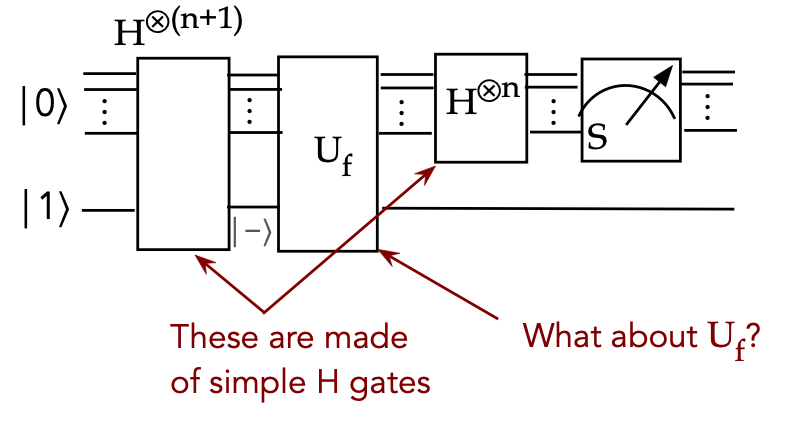
- At the moment it's not clear how one would construct
such a circuit.
- The purpose of the Oracle algorithms, however, is different:
- It is NOT to actually design useful circuits
- The existences of \(U_f\) is assumed
- The goal is to use this assumption to
stimulate the design of algorithmic ideas and building blocks