\( \newcommand{\blah}{blah-blah-blah} \newcommand{\eqb}[1]{\begin{eqnarray*}#1\end{eqnarray*}} \newcommand{\eqbn}[1]{\begin{eqnarray}#1\end{eqnarray}} \newcommand{\bb}[1]{\mathbf{#1}} \newcommand{\mat}[1]{\begin{bmatrix}#1\end{bmatrix}} \newcommand{\nchoose}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array}\right)} \newcommand{\defn}{\stackrel{\vartriangle}{=}} \newcommand{\rvectwo}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array}\right)} \newcommand{\rvecthree}[3]{\left(\begin{array}{r} #1 \\ #2\\ #3\end{array}\right)} \newcommand{\rvecdots}[3]{\left(\begin{array}{r} #1 \\ #2\\ \vdots\\ #3\end{array}\right)} \newcommand{\vectwo}[2]{\left[\begin{array}{r} #1\\#2\end{array}\right]} \newcommand{\vecthree}[3]{\left[\begin{array}{r} #1 \\ #2\\ #3\end{array}\right]} \newcommand{\vecfour}[4]{\left[\begin{array}{r} #1 \\ #2\\ #3\\ #4\end{array}\right]} \newcommand{\vecdots}[3]{\left[\begin{array}{r} #1 \\ #2\\ \vdots\\ #3\end{array}\right]} \newcommand{\eql}{\;\; = \;\;} \definecolor{dkblue}{RGB}{0,0,120} \definecolor{dkred}{RGB}{120,0,0} \definecolor{dkgreen}{RGB}{0,120,0} \newcommand{\bigsp}{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \newcommand{\plss}{\;\;+\;\;} \newcommand{\miss}{\;\;-\;\;} \newcommand{\implies}{\Rightarrow\;\;\;\;\;\;\;\;\;\;\;\;} \newcommand{\prob}[1]{\mbox{Pr}\left[ #1 \right]} \newcommand{\exval}[1]{\mbox{E}\left[ #1 \right]} \newcommand{\variance}[1]{\mbox{Var}\left[ #1 \right]} \newcommand{\kt}[1]{\left\vert #1 \right\rangle} \newcommand{\br}[1]{\left\langle #1 \right\vert} \newcommand{\bkt}[2]{\left\langle #1 \middle\vert #2 \right\rangle} \newcommand{\inr}[2]{\left\langle #1 \middle\vert #2 \right\rangle} \newcommand{\inrs}[2]{\left\langle #1 \: \middle\vert\: #2 \right\rangle} \newcommand{\inrh}[2]{ \left\langle \vphantom{\huge x} #1 \: \middle\vert \: #2 \right\rangle } \newcommand{\swich}[3]{\left\langle #1 \middle\vert #2 \middle\vert #3\right\rangle} \newcommand{\swichs}[3]{\left\langle #1 \:\middle\vert \: #2 \: \middle\vert \: #3\right\rangle} \newcommand{\swichh}[3]{\left\langle \vphantom{\huge x} #1 \;\middle\vert \; #2 \; \middle\vert \; #3\right\rangle} \newcommand{\otr}[2]{\left\vert #1 \right\rangle\!\left\langle #2 \right\vert} \newcommand{\pss}{\large\psi} \newcommand{\re}{\mbox{Re }} \newcommand{\im}{\mbox{Im }} \newcommand{\mag}[1]{\left\vert #1 \right\vert} \newcommand{\magsq}[1]{{\left\vert #1 \right\vert}^2} \newcommand{\magsqh}[1]{{\left\vert \vphantom{\huge x} #1 \right\vert}^2} \newcommand{\isqt}[1]{\frac{#1}{\sqrt{2}}} \newcommand{\mbx}[1]{\;\;\;\;\;\;\;\;{\scriptsize \color{Gray}{\mbox{ #1}}}} \newcommand{\ksi}{\kt{\psi}} \newcommand{\parenh}[1]{\left( \vphantom{\huge x} #1 \right)} \newcommand{\parenl}[1]{\left(\vphantom{\LARGE x} #1 \,\right)} \newcommand{\khi}{\kt{\phi}} \newcommand{\cnot}{C_{\scriptsize NOT}} \newcommand{\setl}[1]{\left\{\vphantom{\LARGE x} #1 \,\right\}} \newcommand{\smm}[1]{\mbox{$ #1 $}} \newcommand{\cz}{C_{\scriptsize Z}} \newcommand{\ccnot}{CC_{\scriptsize NOT}} \newcommand{\ccz}{CC_{\scriptsize Z}} \newcommand{\sml}[1]{{\scriptsize #1}} \newcommand{\smm}[1]{\mbox{$ #1 $}} \newcommand{\smml}[1]{ {\scriptsize{\mbox{$#1$}} } } \newcommand{\smb}[1]{ {\tiny{\mbox{$#1$}} } } \newcommand{\exps}[1]{\exp ({\scriptsize #1} )} \newcommand{\isqts}[1]{\smm{\frac{#1}{\sqrt{2}}}} \newcommand{\halfsm}{\smm{\frac{1}{2}}} \newcommand{\smf}[2]{\mbox{$ \frac{#1}{#2} $}} \)

Module 8 Solved Problems

Problem:
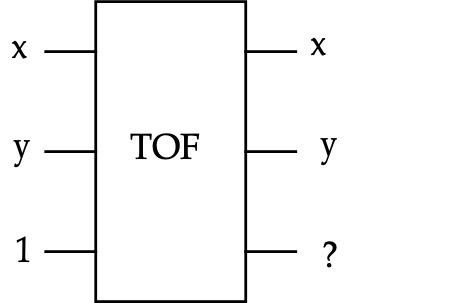
Consider the following inputs to the classical Toffoli gate:

What 2-input function of $x,y$ describes the third output?

Solution:
Recall that $$ \mbox{TOF}\kt{x,y,z} \eql \kt{x,y, xy\oplus z} $$ and so $$ \mbox{TOF}\kt{x,y,1} \eql \kt{x,y, xy\oplus 1} \eql \kt{x,y, (xy)^\prime} $$ This is the Boolean NAND gate, which we can see perhaps more clearly through this truth table: $$ \begin{array}{|c|c|c|c|c|}\hline x & y & xy & (xy)^\prime & xy\oplus 1 \\\hline 0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 0 \\\hline \end{array} $$

Problem:
Is the following a plausible quantum gate?

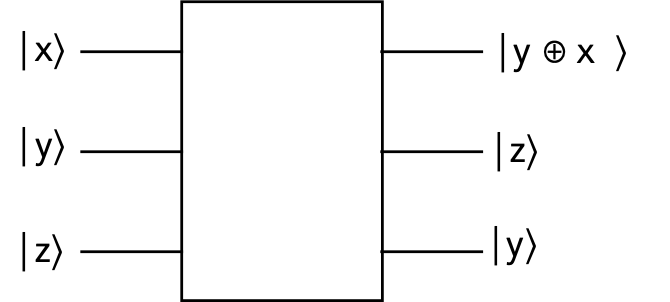
Solution:
Let's write out the truth-table: \begin{array}{|c|c|c|c|c|c|}\hline x & y & z & y\oplus x & z & y\\\hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 \\\hline \end{array} $$ There are no duplicate rows in the output, making this a reversible Boolean function (a permutation), which means a quantum equivalent is theoretically feasible.

As a further exercise to try on your own, suppose $G\kt{x}\kt{y}\kt{z} = \kt{y\oplus x}\kt{z}\kt{y}$. Compute the effect of $G^3$ algebraically. What do you conclude?