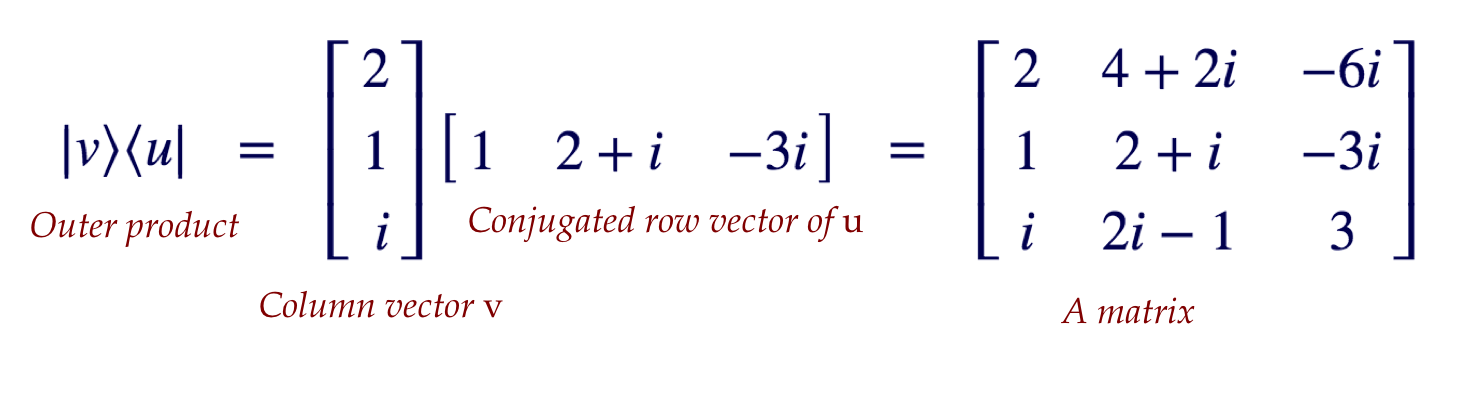Module 2: Highlights (abbreviated)

• Complex numbers:
  • Either \(z = a + ib\) or \(z = re^{i\theta}\)
  • Conjugate: \(z^* = a - ib = re^{-i\theta}\)
  • Euler's: \(e^{i\theta} = \cos\theta + i \sin\theta\)
  • Rules for arithmetic.
  • From which, (complex-valued) functions \(f(z)\)

• Complex vectors:
  • Complex numbers as vector elements $$ \kt{u} \eql \mat{1\\ 2-i\\ 3i} \;\;\;\;\;\; \kt{v} = \mat{2 \\ 1\\ i} $$
  • Conjugated row-vector: $$\eqb{ \br{u} & \eql & \kt{u}^\dagger & \eql & \mat{1 & 2+i & -3i} \\ \br{v} & \eql & \kt{v}^\dagger & \eql & \mat{2 & 1 & -i} }$$
  • Inner-product conjugates left side: $$ \inr{u}{v} \eql \mat{1 & 2+i & -3i} \mat{2 \\ 1\\ i} \eql 7+i \;\;\;\; \mbx{A number} $$
  • Squared-magnitude (not length) of a complex vector: \(\magsq{u} = \inr{u}{u}\)
  • Outer-product: column times row

    

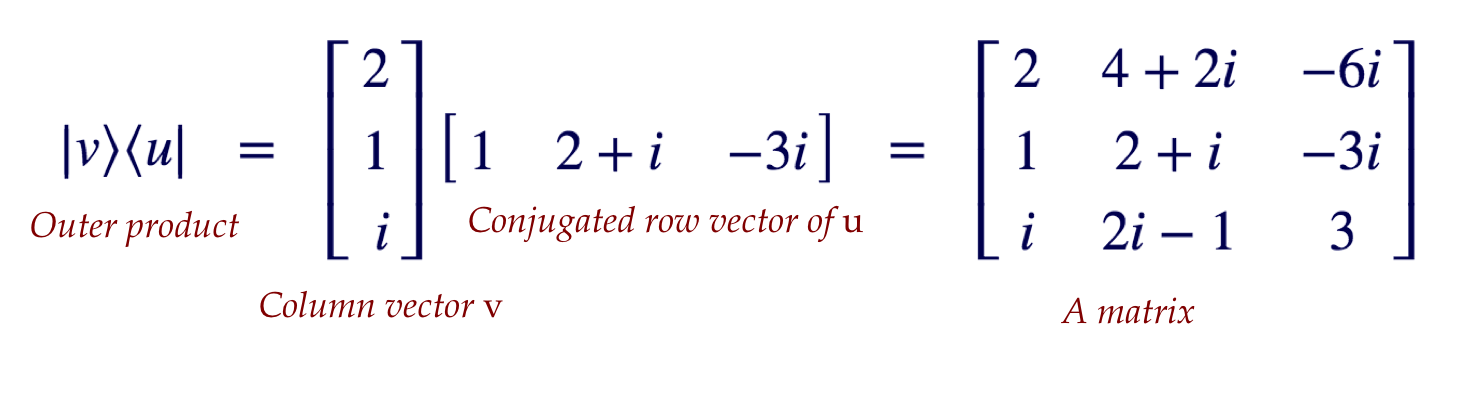
  • Scalar rules: \(\kt{\alpha v} = \alpha\kt{v}\) and \(\br{\alpha v} = \alpha^* \br{v}\)
  • Inner products with linear combinations: $$\eqb{ \inrs{u}{\alpha v + \beta w} & \eql & \alpha\inr{u}{v} + \beta\inr{u}{w} & \mbx{Linearity on the right}\\ \inrs{\alpha u + \beta v}{w} & \eql & \alpha^*\inr{u}{w} + \beta^*\inr{v}{w} & \mbx{Conjugate linearity on the left}\\ }$$

Orthogonality, projectors:

• Vector orthogonality (defined as): \(\inr{u}{v} = 0\)

• Orthonormal:
  • \(\inr{u}{v} = 0\)
  • And \(\mag{u} = \mag{v} = 1\)

• A few important special 2D vectors: $$\eqb{ \kt{0} & \eql & \mat{1\\ 0} & \;\;\;\;\;\; & \kt{1} & \eql & \mat{0\\ 1}\\ \kt{+} & \eql & \mat{\isqt{1}\\ \isqt{1}} & \;\;\;\;\;\; & \kt{-} & \eql & \mat{\isqt{1}\\ -\isqt{1}} }$$

• Projections and projectors:
  • Let \(\kt{v_1},\kt{v_2},\ldots\) be an orthonormal basis.
  • The projector for \(\kt{v_1}\) (a matrix) is: $$ P_{v_1} \eql \otr{v_1}{v_1} $$
  • The projection of any \(\kt{u}\) on \(\kt{v_1}\): $$\eqb{ P_{v_1} \kt{u} & \eql & \otr{v_1}{v_1} \kt{u} & \mbx{Apply projector} \\ & \eql & \kt{v_1} \; \inr{v_1}{u} & \mbx{Associativity} \\ & \eql & \inr{v_1}{u} \; \kt{v_1} & \mbx{Scalar movement} \\ }$$ The number \(\inr{v_1}{u}\) is the coefficient of projection.
  • A vector is the sum of its projections: $$ \kt{u} \eql \parenl{ \inr{v_1}{u} } \: \kt{v_1} + \ldots + \parenl{ \inr{v_n}{u} } \: \kt{v_n} $$
  • Projectors of a basis add up to the identity (completeness relation): $$ \otr{v_1}{v_1} + \ldots + \otr{v_n}{v_n} \eql I $$

Operators:

• 3 types of operators: Hermitian, projectors, unitary
  • Hermitian: \(A = A^\dagger\)

    For example $$ A \eql \mat{1 & -i\\ i & 1} $$ is Hermitian while $$ B \eql \mat{i & 1\\ 1 & -i} $$ is not.

  • Unitary: when \(A A^\dagger = A^\dagger A = I\)

    For example $$ H \eql \mat{\isqt{1} & \isqt{1}\\ \isqt{1} & -\isqt{1}} $$ is unitary because \(H^\dagger H = H H^\dagger = I\)
    But $$ A \eql \mat{1 & -i\\ i & 1} $$ is not.

  • Projector: given a basis \(\kt{v_1},\kt{v_2}\ldots\kt{v_n}\), a projector for \(\kt{v_i}\) is the outer-product $$ P_{v_1} \eql \otr{v_i}{v_i} $$

• Generalizing from real counterparts:
  • Hermitian generalizes real-symmetric
  • Projector works the same in complex/real
  • Unitary generalizes real-orthonormal

• "Dagger" properties:
  1. \(\br{Ax} = \br{x} A^\dagger = \kt{A x}^\dagger\)
  2. \(\br{A^\dagger x} = \br{x} A\)
  3. \( \inr{w}{Ax} = \inr{A^\dagger w}{x}\)
  4. \( \inr{Aw}{x} = \inr{w}{A^\dagger x}\)
  5. \( (A^\dagger)^\dagger = A\)
  6. \( (\alpha A)^\dagger = \alpha^* A^\dagger\)
  7. \( (A + B)^\dagger = A^\dagger + B^\dagger\)
  8. \( (AB)^\dagger = B^\dagger A^\dagger\)

• Hermitian properties: if \(A,B\) are Hermitian
  1. \(A + B\) is Hermitian.
  2. \(\alpha A\) is Hermitian for real numbers \(\alpha\).
  3. \(A\)'s diagonal elements are real numbers.
  4. \(A\)'s eigenvalues are real numbers.
  5. (Spectral theorem): one can find orthonormal eigenvectors that are a basis.
  6. \(A\) can be written in terms of projectors made from the eigenvectors: \(A = \sum_{i=1}^n \lambda_i \otr{v_i}{v_i}\).

• Properties of unitary operators: if \(A, B\) are unitary
  1. \(\inr{Au}{Av} = \inr{u}{v}\) (preserves inner products).
  2. \(|Au| = |u|\) (preserves lengths).
  3. \(A^\dagger\) and \(A^{-1}\) are also unitary.
  4. The columns of \(A\) are orthonormal, as are the rows.
  5. \(AB\) and \(BA\) are unitary.

• Operator sandwich:
  • \(\swich{u}{A}{v} = \inrs{u}{Av} = \inrs{A^\dagger u}{v}\)
  • Applied to a projector: \(\swich{u}{P_v}{u} = \magsq{\inr{v}{u}} = \magsq{P_v\kt{u}} \)

• Basis of the moment:
  • Vectors exist as mathematical objects without the numbers in them.
  • To put numbers to (i.e., "numerify") a vector, a basis must be selected.
  • It's much easier to select an orthonormal basis (any orthonormal basis).
  • We generally use the standard basis.
  • But some books will use the eigenbasis, which makes some calculations easier.

• Review of important and special 2D vectors: $$\eqb{ \kt{0} & \eql & \mat{1\\ 0} & & \\ \kt{1} & \eql & \mat{0\\ 1} & & \\ \kt{+} & \eql & \vectwo{ \isqt{1} }{ \isqt{1} } & \eql & \isqt{1} \mat{1\\ 0} \: + \: \isqt{1} \mat{0\\ 1} \\ \kt{-} & \eql & \vectwo{ \isqt{1} }{ -\isqt{1} } & \eql & \isqt{1} \mat{1\\ 0} \: - \: \isqt{1} \mat{0\\ 1} \\ }$$ Useful-to-know relationships between these: $$\eqb{ \kt{+} & \eql & \isqt{1} \kt{0} \: + \: \isqt{1} \kt{1} \\ \kt{-} & \eql & \isqt{1} \kt{0} \: - \: \isqt{1} \kt{1} \\ \kt{0} & \eql & \isqt{1} \kt{+} \: + \: \isqt{1} \kt{-} \\ \kt{1} & \eql & \isqt{1} \kt{+} \: - \: \isqt{1} \kt{-} \\ }$$