Module objectives
The main goals of this module:
- To better understand abstract linear algebra by seeing how it
works for more abstract vectors, in particular "continuous" vectors.
- To peer into quantum mechanics, the field that underlies
and accompanies quantum computing.
- To explore some of the strange and popular stories about quantum
mechanics, such as Schrodinger's cat.
11.1
Discrete quantum mechanics
Let's start by casting quantum computing in terms of
a discrete formulation of quantum mechanics:
- What is the system under consideration?
\(\rhd\)
In our case: a group of qubits
- The system at any time is in some state represented
by a vector:
\(\rhd\)
Example: \(\ksi\) = the current state of n qubits
- A state can change in only one of two ways:
- A unitary operation
- A measurement.
- A unitary operation is represented by a unitary matrix.
- A measurement is represented either by:
- A collection of projectors, one per subspace.
- Or a Hermitian that packages the projectors.
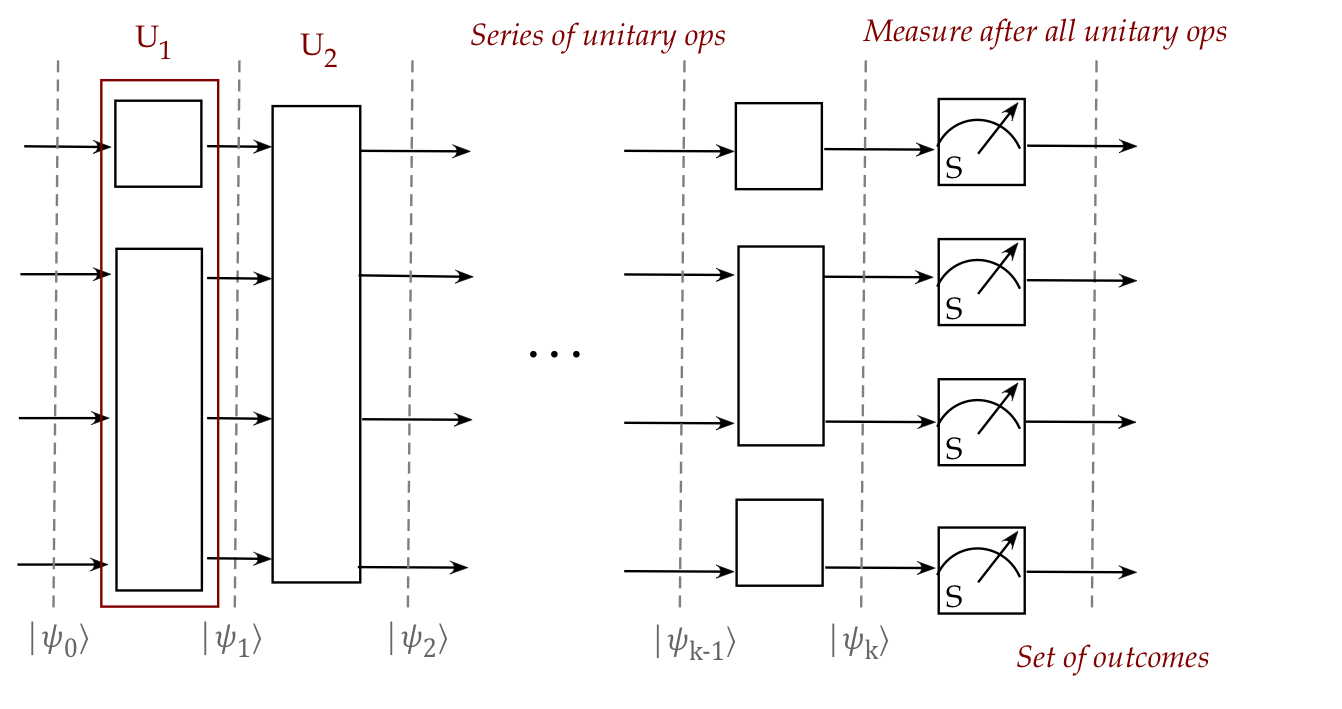
- In the standard model, a collection of unitary operators
\(U_1, U_2,\ldots U_k\)
are applied to a starting state \(\kt{\psi_0}\):
$$\eqb{
\kt{\psi_1} & \eql & U_1 \kt{\psi_0} \\
\kt{\psi_2} & \eql & U_2 \kt{\psi_1} \\
& \vdots & \\
\kt{\psi_k} & \eql & U_k \kt{\psi_{k-1}} \\
}$$
And then, measurement is performed on the end state \(\kt{\psi_k}\):
- Pictorially:
- The only additional feature of the theory not
obvious above is entanglement and the effect
of measurement on an entangled vector:
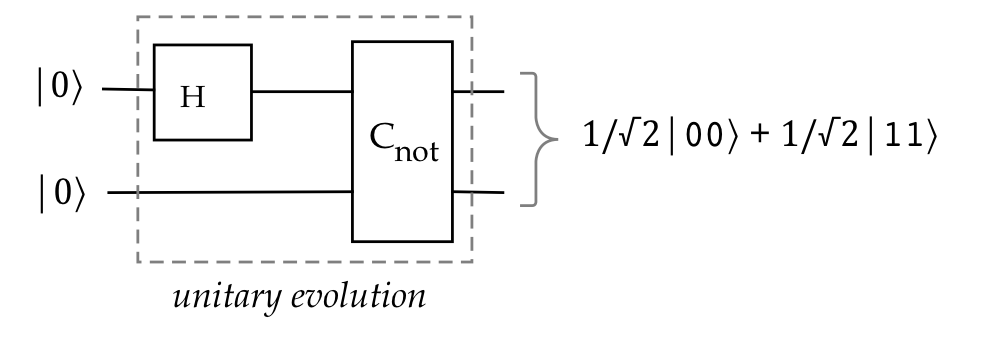
- For example, suppose a 1-qubit (Alice's) measurement
is performed on
$$
\ksi \eql \isqts{1} \parenl{ \kt{00} + \kt{11} }
$$
- The 1-qubit measurement is really a 2-qubit measurement
using two projectors, \(\otr{0}{0} \otimes I\) and
\(\otr{1}{1} \otimes I\).
- This will result in one of two 2-qubit states:
\(\kt{00}\) or \(\kt{11}\)
- The result is that further measurement on Bob's
side is completely determined.
- In some sense, this is a complete theory of
discrete quantum mechanics:
\(\rhd\)
There is no other (discrete) phenomenon to describe.
- However, it is not enough to describe everything
else in nature, just the abstract qubits in quantum computing
and their behavior.
But even a supposedly complete theory may have holes:
- For example, how is one to explain
the instantaneous effect of Alice's measurement on Bob's qubit?
11.2
The EPR paradox, hidden variables and Bell's theorem
In 1935, Einstein, Podolsky and Rosen (EPR) wrote a
landmark critique of quantum theory:
- They said any valid theory must have two features:
- Realism.
Any theory that perfectly predicts some physically observable
quantity must have a variable in it that tracks or computes that quantity.
- Locality.
Nature acts locally and physical influences are subject to the speed of
light limitation.
- But the Alice-Bob measurement of an entangled pair
shows that:
- After Alice's measurement, quantum theory
predicts Bob's outcome exactly.
- This is instantaneous no matter the distance between
Alice and Bob.
- Thus, quantum theory's realism is decidedly nonlocal.
- Therefore, according to EPR, quantum theory is incomplete
because it does not have corresponding variables that exhibit
locality in this case.
- For example, is it possible that Alice's and Bob's
qubits carry in them some hidden state?
- Perhaps science is not advanced enough to see or probe
the hidden state.
- And yet the hidden state determines the outcomes.
- After all, the history is science is rife with examples where
some underlying scale-dependent quantity was unknown to
some fairly successful theories
\(\rhd\)
Example: Newtonian mechanics (not accurate when scaled to
high velocity)
- This seeming contradiction in the theory itself was
referred to (historically) as the EPR paradox.
\(\rhd\)
It is no longer considered a paradox today.
Let's now suppose there exist local hidden variables, that
travel with the qubits:
- We will show that any theory with such variables will
predict outcomes different from quantum theory.
- Because quantum theory's predictions match experimental
results, any such theory must be rejected.
- The reasoning is delicate and requires many steps, which
we will undertake in the next few sections.
- The findings about hidden variables have been generalized
into a collection of results called Bell's Inequalities:
- Each inequality is something that must be satisfied by
a local (hidden-variable) theory.
- But quantum theory is shown to violate such inequalities.
- The inequalities are named for John Bell, the physicist
who derived the first of them, which eventually led to a proof
(experimentally) that E, P, and R were wrong.
11.3
Hidden variables, part I: measuring polarization
First, let's recall the use of the sandwich for projectors:
- For any \(\ksi\) and projector \(P\), we know that
$$
\mbox{Probability of seeing outcome \(P\ksi\)}
\eql \magsq{P\ksi}
$$
- An alternative way to calculate this probability is to
write it as a projector sandwich:
$$
\mbox{Probability of seeing outcome \(P\ksi\)}
\eql \swich{\psi}{P}{\psi}
$$
(See Module 2).
- Doing so enables exploiting Dirac-notation inner-products, as
we'll see when we work out the details.
Now consider this set up:
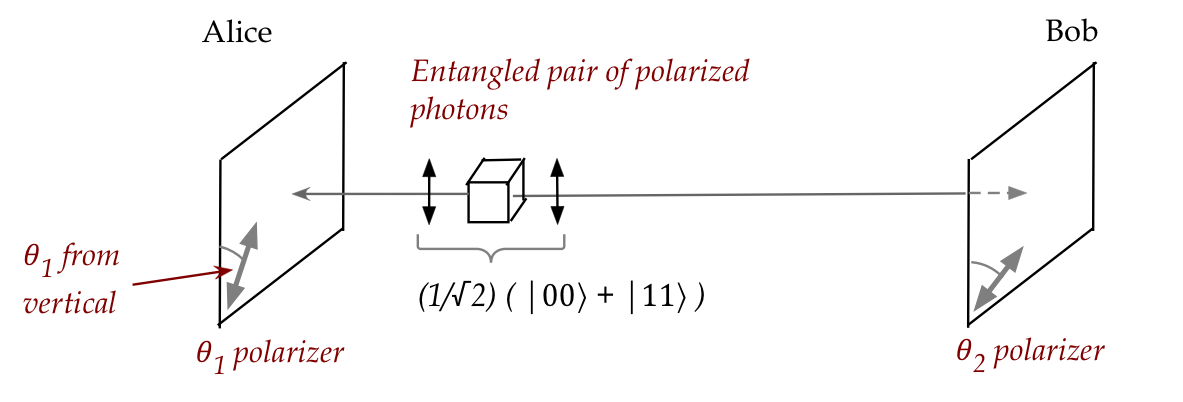
- A device generates EPR photon-pairs whose polarizations are
entangled in the first Bell state:
$$
\ksi \eql \isqts{1} \parenl{ \kt{00} + \kt{11} }
$$
where
- \(\kt{0}\) represents vertical polarization
- \(\kt{1}\) represents horizontal
- Alice measures first, using a polarizer oriented at
angle \(\theta_1\).
- Bob later measures with polarizer at \(\theta_2\)
from the vertical.
- Qualitatively, what are the outcomes?
- For Alice, her photon either passes (P) or gets absorbed (A).
- Same for Bob.
- We will be interested in these two cases:
- Agreement:
- If Alice's photon passes, so does Bob's (P-P)
- If Alice's photon is absorbed, so is Bob's (A-A).
- Disagreement: different results on their photons.
(P-A, A-P).
As a first step, let's consider how a single photon
behaves when a polarizer is oriented at an angle:
- Suppose this basis is represented by
$$\eqb{
\kt{v} & \equiv & \;\; \mbox{Pass through} \\
\kt{v^\perp} & \equiv & \;\; \mbox{Absorb} \\
}$$
- For the photon, we'll use
$$\eqb{
\kt{0} & \equiv & \;\; \mbox{Vertically polarized} \\
\kt{1} & \equiv & \;\; \mbox{Horizontally polarized} \\
}$$
- Consider a vertically polarized photon (in state
\(\kt{0}\)) arriving at a \(\theta\)-filter.
- It will be convenient to express the filter's
\(\kt{v},\kt{v^\perp}\) basis vectors in terms of
the standard basis \(\kt{0},\kt{1}\).
- When \(\theta=0\), we already know that
$$\eqb{
\kt{v} & \eql & \kt{0} & \mbx{Vertical photons pass through with probability 1} \\
\kt{v^\perp} & \eql & \kt{1} & \mbx{They get absorbed with probability 0}
}$$
- Even though \(\kt{v}, \kt{v^\perp}\) are technically
complex vectors, the particular ones so far are real-valued,
which will allow us to draw (using real coordinates):
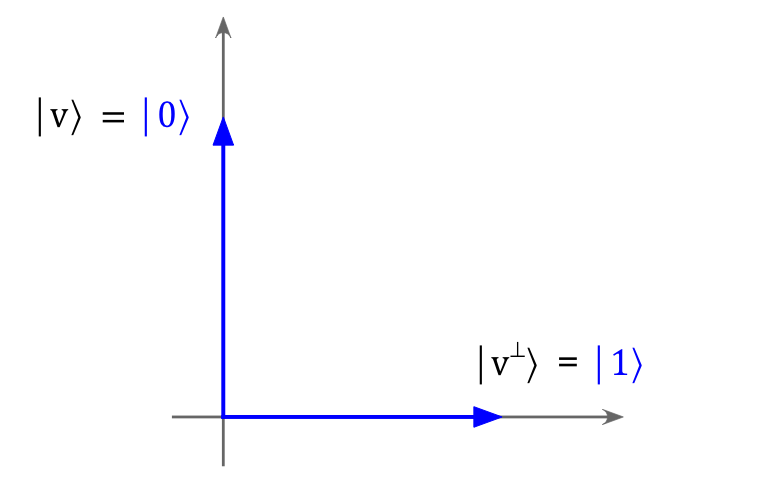
- Let's work through measurement in the \(\theta=0\) case:
- Here, \(\kt{v}=\kt{0},\kt{v^\perp}=\kt{1}\).
- Now express the incoming photon \(\kt{0}\) in terms
of the \(\theta=0\) filter's basis:
$$
\mbox{photon } \;\; \kt{0} \eql 1 \cdot \kt{0} + 0 \kt{1}
\;\;\;\;\; \mbox{Measurement basis on right side}
$$
- Then, the outcome state is \(\kt{v}=\kt{0}\) with probability \(1\).
- Thus, for vertical photons,
$$\eqb{
\mbox{With vertical filter} \;\; \kt{v} = \kt{0} & \Rightarrow & \mbox{Pr[pass through]=1} \\
\mbox{With vertical filter} \;\; \kt{v^\perp} = \kt{1}
& \Rightarrow & \mbox{Pr[absorb]=0} \\
}$$
- Similarly, if \(\theta=\frac{\pi}{2}\) (horizontal filter),
then one can depict \(\kt{v}, \kt{v^\perp}\) as:
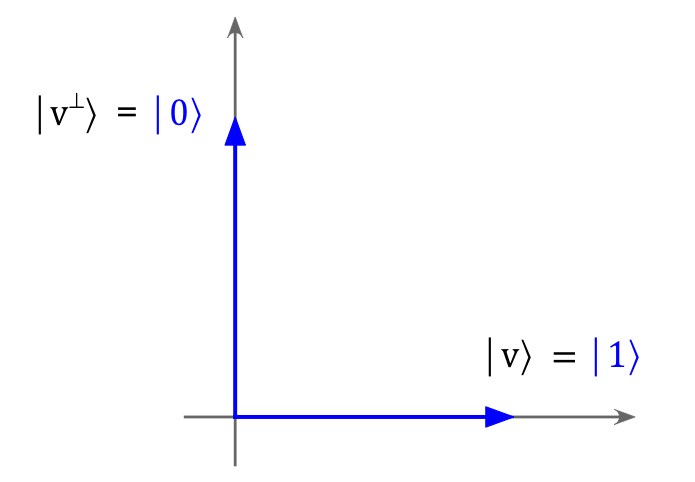
In this case, the filter basis is:
$$\eqb{
\kt{v} & \eql & \kt{1} \\
\kt{v^\perp} & \eql & \kt{0} \\
}$$
And so, for vertical photons:
$$
\mbox{photon } \;\; \kt{0} \eql 0\cdot \kt{1} + 1\cdot \kt{0}
$$
That is, outcome state is \(\kt{v^\perp} = \kt{0}\) and so
$$\eqb{
\mbox{With horizontal filter} \;\; \kt{v} = \kt{1} & \Rightarrow & \mbox{Pr[pass through]=0} \\
\mbox{With horizontal filter} \;\; \kt{v^\perp} = \kt{0}
& \Rightarrow & \mbox{Pr[absorb]=1} \\
}$$
- One expects a high probability of pass-through for angles
near \(\theta=0\), and low probability for angles near
\(\theta=\frac{\pi}{2}\).
- So, for a generic \(\theta\), we can use the (real-coordinate)
geometry to intuit \(\kt{v}, \kt{v^\perp}\) in terms of
\(\kt{0}, \kt{1}\):
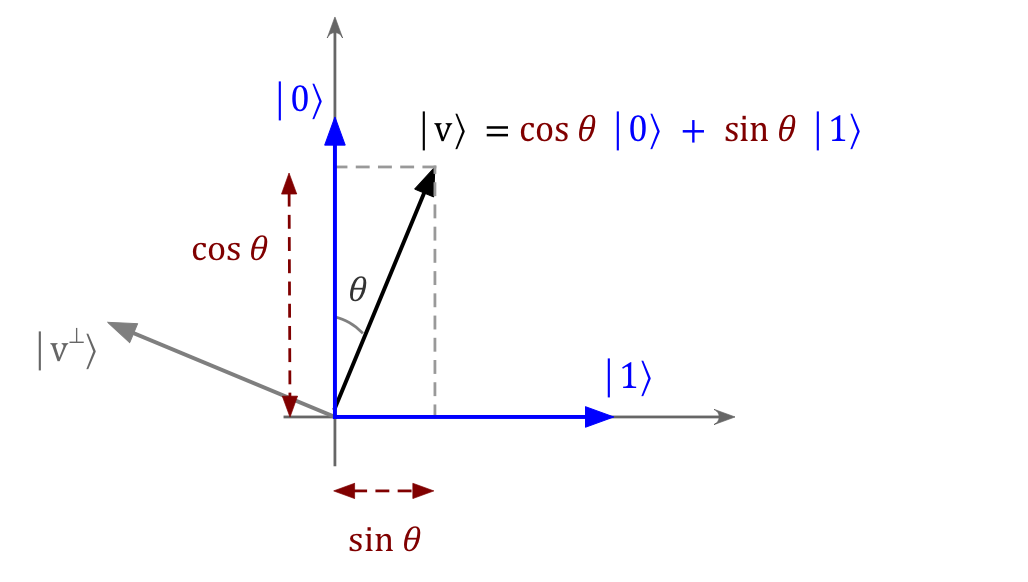
From the geometry:
$$\eqb{
\kt{v} & \eql & \cos\theta\kt{0} + \sin\theta\kt{1}
& \equiv & \mbox{Pass through} \\
\kt{v^\perp} & \eql & \sin\theta\kt{0} - \cos\theta\kt{1}
& \equiv & \mbox{Absorb} \\
}$$
- Aside:
$$
\kt{v^\perp} \eql -\sin\theta\kt{0} + \cos\theta\kt{1}
$$
would work just as well.
- Let's confirm orthonormality by recalling
the general case:
$$
\kt{v} \eql \alpha\kt{0} + \beta\kt{1}
$$
Then if
$$
\kt{v^\perp} \eql \beta^*\kt{0} - \alpha^*\kt{1}
$$
both \(\kt{v}\) and \(\kt{v^\perp}\) are an orthonormal basis
because
$$
\inr{v^\perp}{v}
\eql
\inrh{ \beta^*\kt{0} - \alpha^*\kt{1} }{ \alpha\kt{0} + \beta\kt{1} }
\eql
\beta\alpha - \alpha\beta
\eql 0
$$
and their lengths are \(1\).
- Thus, we see that with
$$\eqb{
\kt{v} & \eql & \cos\theta\kt{0} + \sin\theta\kt{1}\\
\kt{v^\perp} & \eql & \sin\theta\kt{0} - \cos\theta\kt{1}
}$$
we get
$$
\inr{v^\perp}{v}
\eql
\inrh{ \sin\theta\kt{0} - \cos\theta\kt{1} }{ \cos\theta\kt{0} +
\sin\theta\kt{1} }
\eql
\sin\theta\cos\theta - \cos\theta\sin\theta
\eql 0
$$
And their lengths are
$$
\cos^2\theta + \sin^2\theta \eql 1
$$
- Let's work through with \(\theta = \frac{\pi}{4}\):
- Then,
$$\eqb{
\kt{v} & \eql & \cos\theta\kt{0} + \sin\theta\kt{1}
& \eql & \isqts{1} \kt{0} + \isqts{1} \kt{1} & \eql & \kt{+}\\
\kt{v^\perp} & \eql & \sin\theta\kt{0} - \cos\theta\kt{1}
& \eql & \isqts{1} \kt{0} - \isqts{1} \kt{1} & \eql & \kt{-}\\
}$$
- This is the Hadamard basis, which we've seen has probability
\(\frac{1}{2}\) for letting a vertically polarized photon pass.
- So far so good, but we need to establish that the
intuitive approach above is actually correct.
Let's work out the the probability of vertical-photon
pass-through for general \(\theta\):
In-Class Exercise 1:
Calculate \(\magsq{P_v\kt{0}}\) directly and
show that it leads to the same result.
Now let's go back to the entangled Alice-Bob set up:
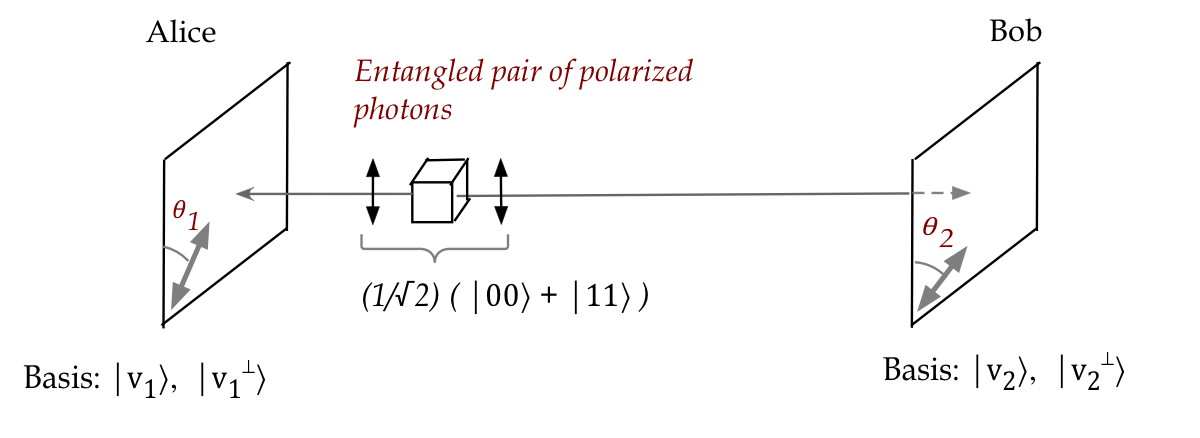
- Since they each use a different angle, we'll distinguish the
two measurement bases.
- Alice's basis is:
$$\eqb{
\kt{v_1} & \eql & \cos\theta_1\kt{0} + \sin\theta_1\kt{1}
& \mbx{Pass} \\
\kt{v_1^\perp} & \eql & \sin\theta_1\kt{0} - \cos\theta_1\kt{1}
& \mbx{Absorb} \\
}$$
-
And Bob's is:
$$\eqb{
\kt{v_2} & \eql & \cos\theta_2\kt{0} + \sin\theta_2\kt{1}
& \mbx{Pass} \\
\kt{v_2^\perp} & \eql & \sin\theta_2\kt{0} - \cos\theta_2\kt{1}
& \mbx{Absorb} \\
}$$
- Now let's apply projective measurement, starting with Alice:
- Alice's measurement has projectors
$$\eqb{
P_{v_1} & \eql & \otr{v_1}{v_1}
& \mbx{Pass} \\
P_{v_1^\perp} & \eql & \otr{v_1^\perp}{v_1^\perp}
& \mbx{Absorb} \\
}$$
- When applied, the resulting 2-qubit measurement projectors
are \(P_{v_1} \otimes I\) and \(P_{v_1^\perp} \otimes I\).
- Similarly, Bob's measurement is described by the two projectors
\(I \otimes P_{v_2}\) and \(I \otimes P_{v_2^\perp}\)
where
$$\eqb{
P_{v_2} & \eql & \otr{v_2}{v_2}
& \mbx{Pass} \\
P_{v_2^\perp} & \eql & \otr{v_2^\perp}{v_2^\perp}
& \mbx{Absorb} \\
}$$
- Thus, in combination, the four possibilities are:
- Both pass (P-P):
$$
\parenl{ I \otimes P_{v_2}} \parenl{ P_{v_1} \otimes I }
\eql
P_{v_1} \otimes P_{v_2}
$$
- Both are absorbed (A-A):
$$
\parenl{ I \otimes P_{v_2^\perp}} \parenl{ P_{v_1^\perp} \otimes I }
\eql
P_{v_1^\perp} \otimes P_{v_2^\perp}
$$
- Alice's photon is absorbed, Bob's passes (A-P):
$$
\parenl{ I \otimes P_{v_2}} \parenl{ P_{v_1^\perp} \otimes I }
\eql
P_{v_1^\perp} \otimes P_{v_2}
$$
- Alice's passes, Bob's is absorbed (P-A):
$$
\parenl{ I \otimes P_{v_2^\perp}} \parenl{ P_{v_1} \otimes I }
\eql
P_{v_1} \otimes P_{v_2^\perp}
$$
- For any 2-qubit state \(\ksi\), the probabilities of these
four events are:
- Both pass: \(\swichh{\psi}{P_{v_1} \otimes P_{v_2}}{\psi}\)
- Both absorb:
\(\swichh{\psi}{P_{v_1^\perp} \otimes P_{v_2^\perp}}{\psi}\)
- Pass-absorb:
\(\swichh{\psi}{P_{v_1} \otimes P_{v_2^\perp}}{\psi}\)
- Absorb-pass:
\(\swichh{\psi}{P_{v_1^\perp} \otimes P_{v_2}}{\psi}\)
- Finally, we can now focus on the probability that both see
the same result:
$$\eqb{
\mbox{Pr[Same result]}
& \eql &
\mbox{Pr[both pass]} \; + \; \mbox{Pr[both are absorbed]} \\
& \eql &
\swichh{\psi}{P_{v_1} \otimes P_{v_2}}{\psi}
\; + \;
\swichh{\psi}{P_{v_1^\perp} \otimes P_{v_2^\perp}}{\psi}
}$$
- What remains: doing the calculation.
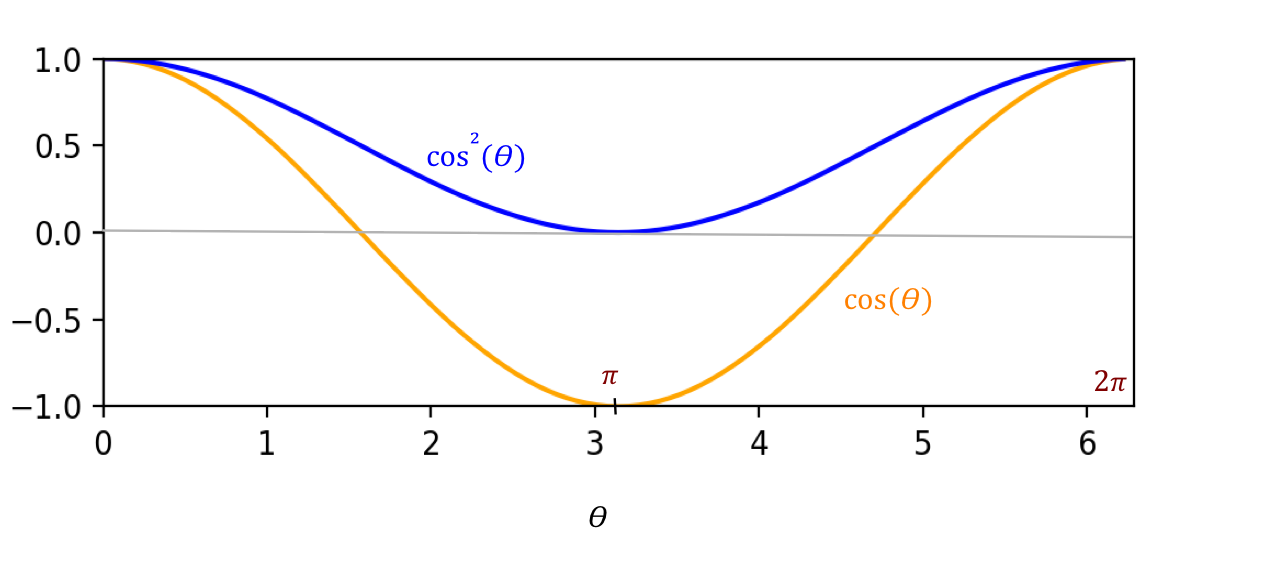
- The calculation shows that
$$
\mbox{Pr[Same result]}
\eql
\cos^2 \parenl{\theta_1 - \theta_2}
$$
Or the other way around: \(\cos^2 (\theta_2 - \theta_1)\)
In-Class Exercise 2:
One of the solved problems shows how to calculate the
result for \(\swich{\psi}{P_{v_1} \otimes P_{v_2}}{\psi}\).
Show how the same approach can be used to calculate
\(\swich{\psi}{P_{v_1^\perp} \otimes P_{v_2^\perp}}{\psi}\),
writing out all 16 terms (just once) for clarity.
Then, complete the steps in showing
\(\mbox{Pr[Same result]} = \cos^2 (\theta_2 - \theta_1)\).
The result comports with intuition:
- When \(\theta_1=0\), Alice's measurement is the standard
basis \(\kt{0},\kt{1}\).
- In this case, the 2-qubit outcome will be one of
\(\kt{00},\kt{11}\).
- Because of this, Bob's measurement at angle \(\theta_2\)
will apply to his qubit which will be in one of \(\kt{0},\kt{1}\).
- Recall that we derived the pass-through probability as
\(\cos^2\theta_2\).
- This is exactly what's predicted: when \(\theta_1=0\),
$$
\cos^2 (\theta_1 - \theta_2) \eql \cos^2 \theta_2
$$
- When the angles are close, \(\theta_1 \approx \theta_2\) we
should get high probability of agreement, which is indeed the case:
$$
\cos^2 (\theta_1 - \theta_2)
\approx
\cos^2 0
\eql 1
$$
In-Class Exercise 3:
What is the probability of agreement when:
- \(\theta_1=-\frac{\pi}{3}, \theta_2=0\)?
- \(\theta_1=\frac{\pi}{3}, \theta_2=-\frac{\pi}{3}\)?
11.4
Hidden variables, part II: what quantum mechanics predicts
With that background, we now move to the interesting part
of the experiment:
- Alice and Bob each choose their angle randomly
from amongst \(-60^\circ, 0, 60^\circ\).
- There are 9 possible cases:
$$
\begin{array}{|c|c|}\hline
\mbox{Alice: } \theta_1 & \mbox{ Bob: } \theta_2 \\\hline
60^\circ & 60^\circ \\
0^\circ & 0^\circ \\
-60^\circ & -60^\circ \\
-60^\circ & 60^\circ \\
-60^\circ & 0^\circ \\
0^\circ & 60^\circ \\
0^\circ & -60^\circ \\
60^\circ & 0^\circ \\
60^\circ & -60^\circ \\\hline
\end{array}
$$
- The probability of agreement in each of the 9 cases
is given by:
\begin{array}{|c|c|}\hline
\mbox{Alice: } \theta_1 & \mbox{ Bob: } \theta_2
& \theta_1 - \theta_2 &
\cos(\theta_1 - \theta_2) & \cos^2(\theta_1 - \theta_2)
\\\hline
60^\circ & 60^\circ & 0 & 1 & 1\\
0^\circ & 0^\circ & 0 & 1 & 1\\
-60^\circ & -60^\circ & 0 & 1 & 1\\
-60^\circ & 60^\circ & -120^\circ & \frac{1}{2} & \frac{1}{4}\\
-60^\circ & 0^\circ & -60^\circ & \frac{1}{2} & \frac{1}{4}\\
0^\circ & 60^\circ & -60^\circ & \frac{1}{2} & \frac{1}{4}\\
0^\circ & -60^\circ & 60^\circ & \frac{1}{2} & \frac{1}{4}\\
60^\circ & 0^\circ & 60^\circ & \frac{1}{2} & \frac{1}{4}\\
60^\circ & -60^\circ & 120^\circ & \frac{1}{2} & \frac{1}{4}\\\hline
\end{array}
- We can summarize this as:
$$
\mbox{Pr[pass/absorb outcomes agree]}
\eql
\left\{
\begin{array}{cc}
1 & \;\;\;\;\; \theta_1 = \theta_2 \\
\frac{1}{4} & \;\;\;\;\; \theta_1 \neq \theta_2 \\
\end{array}
\right.
$$
- Since Alice and Bob pick their angles randomly, any of
the 9 configurations above is equally likely to occur.
- Thus, the probability of agreement is:
$$\eqb{
\mbox{Pr[agree]}
& \eql &
\mbox{Pr[agree|\(\theta_1=\theta_2\)]}
\, \mbox{Pr[\(\theta_1=\theta_2\)]}
\; + \;
\mbox{Pr[agree|\(\theta_1\neq\theta_2\)]}
\, \mbox{Pr[\(\theta_1\neq\theta_2\)]} \\
& \eql &
1 \cdot \smf{3}{9} \; + \; \smf{1}{4} \cdot \smf{6}{9} \\
& \eql &
\smf{1}{2}
}$$
11.5
Hidden variables, part II: What hidden variables predict
We now suppose each photon in an entangled pair carries
in it some local hidden state, inaccessible to quantum theory:
- If this is true, then the following must be true:
- Since the photons are identical, it must be the same
variable in each but with possibly different values.
- The action of pass/absorb must depend on this variable,
otherwise we're just left with quantum theory.
- The action is local, by assumption.
- Let's look a little more closely at the locality assumption:
- If locality is true, then the value of the carried variable
at Alice can have no influence on what occurs at Bob's end.
(And vice-versa.)
- Also, if the value happens to be the same for each photon,
we should observe the
same outcome (whether pass or absorb)
- Next, there is another assumption that comes with
buying into local-hidden-variables:
- The entangled pair is the Bell state
\(\isqt{1} \parenl{ \kt{00} + \kt{11} }\)
- If we simply switched the photons sent to Alice and Bob,
we should see the same statistical results.
- That is, send the "right" photon to Alice, the "left" to Bob.
- The photons are considered identical, at least in reacting
to a filter.
- The consequence of "identical reaction" is:
- The hidden states that travel with the two photons are identical.
- Thus, both should react the same way (pass or absorb)
when encountering the same polarizer angle.
Now let's analyze what happens with hidden variables:
- First, consider the possibilities when a hidden
variable "encounters" a filter set at one of the three angles.
- For any given angle, a hidden variable produces
either "pass" or "absorb".
- Thus, for the three angle choices, a particular
hidden variable must have three outcomes from one
of the rows in:
$$
\begin{array}{|c|c|c|}\hline
-60^\circ & 0 & 60^\circ \\\hline
P & P & P \\
{\bf P} & {\bf P} & {\bf A} \\
P & A & P \\
P & A & A \\
A & P & P \\
A & P & A \\
A & A & P \\
A & A & A \\\hline
\end{array}
$$
where P = pass, and A = absorb.
- For example, consider the 2nd row: P P A.
- This is saying that the hidden variable happens to have the
effect:
- Pass when \(\theta=-60^\circ\)
- Pass when \(\theta=0^\circ\)
- Absorb when \(\theta=60^\circ\)
- To summarize:
whatever the particular state of the hidden variable (or variables),
the outcomes will be one of the rows in the above table.
- Then, we could call a hidden state a PPA-state if
it has the effect described in the second row (PPA).
- So, there are 8 types of pairs: PPP, PPA, PAP, PAA, APP,
APA, AAP, AAA.
- In any particular experiment, one of these types will arrive
at Alice and Bob.
- Now let's return to the 9 possible angle configurations
and focus only on the PPA state.
- We'll ask the question: what happens when two identical
PPA photons encounter randomly chosen angles from
\(-60^\circ, 0, 60^\circ\)?
- First, let's note what identical-PPA means:
$$
\begin{array}{|l|c|c|c|}\hline
\; & -60^\circ & 0 & 60^\circ \\\hline
\mbox{Alice's photon} & P & P & A \\
\mbox{Bob's photon} & P & P & A \\\hline
\end{array}
$$
For example, suppose Alice has set her angle \(\theta_1=0\)
and Bob has set \(\theta_2=60^\circ\):
- The left (Alice's) PPA photon will pass.
- The right (Bob's) PPA photon will be absorbed.
- We can describe every one of the possible outcomes
in a table that shows all the 9 angle settings:
$$
\begin{array}{|c|c|}\hline
\mbox{Alice: } \theta_1 & \mbox{ Bob: } \theta_2
& \mbox{Alice's photon}
& \mbox{Bob's photon}
& \mbox{Agreement} \\\hline
60^\circ & 60^\circ & A & A & agree \\
0^\circ & 0^\circ & P & P & agree \\
-60^\circ & -60^\circ & P & P & agree \\
-60^\circ & 60^\circ & P & A & \\
-60^\circ & 0^\circ & P & P & agree \\
0^\circ & 60^\circ & P & A & \\
0^\circ & -60^\circ & P & P & agree \\
60^\circ & 0^\circ & A & P \\
60^\circ & -60^\circ & A & P \\\hline
\end{array}
$$
So, a PPA pair of photons will agree 5/9-ths of the time.
- We can work out such tables for all 8 types of
photons.
In-Class Exercise 4:
Write out the table for APA photons (when both are APA)
and for AAA photons (when both are AAA).
Let's continue the analysis:
- For PPP and AAA pairs,
the probability of agreement is \(1\).
- For all others, the probability of agreement is
\(\frac{5}{9}\).
- Because these are hidden variables, we cannot make any
assumptions about which states occur more frequently and
how they occur.
- But we can state confidently that: the probability of
agreement is at least \(\frac{5}{9}\).
- So, now we have two theories with differing predictions
of photon-action-agreement (pass or absorb):
- Quantum theory:
$$
\mbox{Pr[agree]} \eql \smf{1}{2}
$$
- Hidden-variable theory:
$$
\mbox{Pr[agree]} \geq \smf{5}{9}
$$
- The latter is an example of a Bell Inequality.
(There are many such experimental designs, each with their
own Bell Inequality.)
- So, who's right?
- The only way to decide: multiple carefully conducted
experiments, repeated and analyzed.
- In all cases tested so far, quantum theory has always
been correct, with very high statistical accuracy.
- That is, there is no known case where quantum theory has
been wrong.
So, what then is quantum mechanics and how does it relate
to what we've seen in quantum computing?
11.6
Towards the continuum, part 1: two types of infinity
Why do we need this extension to the continuum?
- For discrete physical phenomena like Stern-Gerlach,
the theory developed so far with linear algebra suffices.
- But most physical quantities of interest are modeled
by real numbers, such as position and momentum.
First, some notational clarification:
- We have been using a subscript to both identify
vector components and index a collection of vectors, as in
$$
\kt{w} \eql \sum_i c_i \kt{v_i}
$$
- Thus, for example if
$$
\kt{w} \eql c_1 \kt{v_1} + c_2 \kt{v_2} + c_3 \kt{v_3}
$$
then in the v-basis
$$
\kt{w} \eql \mat{c_1 \\ c_2 \\ c_3}
$$
- Thus \(c_i\) (as in \(c_1, c_2, c_3\)) refer to coefficients
in a linear combination
- Or, equivalently,
vector components when expressing \(\kt{w}\) in the v-basis.
- And with \(\kt{v_i}\), the subscript \(i\) refers
to which vector in the collection.
- This dual-use of subscripts did not matter in the discrete
case because \(n\)-component vectors need an \(n\)-vector basis.
- But in the continuous case, it will be different.
- Let's rewrite the discrete version to separate out
components from collections:
- We'll write
$$
\kt{w} \eql c(1) \kt{v_1} + c(2) \kt{v_2} + c(3) \kt{v_3}
$$
- Here, we use parentheses for components, and subscripts for
indexing something from a collection:
$$\eqb{
c(i) & \eql & \mbox{\(i\)-th component of } \kt{w}
& \eql & \mbox{\(i\)-th coefficient in linear-comb }\\
v_i & \eql & \mbox{\(i\)-th vector in a basis }
\kt{v_1},\ldots,\kt{v_n} & & \\
}$$
- This way, we can even refer to the components of each
\(\kt{v_i}\) as in:
$$
w(1) \eql c(1) v_1(1) + c(2) v_2(1) + c(3) v_2(1)
$$
where
$$
v_i(j) \eql \mbox{\(j\)-th component of vector} \kt{v_i} \\
$$
- With this slightly changed notation, let's point out:
- We've written
$$
\kt{w} \eql \sum_i c(i) \kt{v_i}
$$
where
$$
c(i) \eql \inr{v_i}{w}
$$
- Recall:
$$
\kt{w} \eql \sum_i \inr{v_i}{w} \, \kt{v_i}
$$
- Let's recall our standard inner-product with our new notation:
- Let
$$\eqb{
\kt{w} & \eql & \sum_i c(i) \kt{v_i} \\
\kt{u} & \eql & \sum_i b(i) \kt{v_i} \\
}$$
be two vectors expressed in the v-basis.
- Then,
$$
\inr{w}{u}
\eql
\inrh{ \sum_j c(j) \kt{v_j} }{ \sum_i b(i) \kt{v_i} }
\eql
\sum_i c^*(i) b(i)
$$
as expected (See Module-2 solved problems.)
- Next, for an orthonormal basis \(\kt{v_1},\ldots,\kt{v_n}\)
$$
\inr{v_i}{v_j}
\eql
\left\{
\begin{array}{cc}
1, & \;\;\;\; i=j \\
0, & \;\;\;\; i\neq j \\
\end{array}
\right.
$$
We'll invent functions \(\delta_i(j)\) where
$$
\delta_i(j)
\eql
\left\{
\begin{array}{cc}
1, & \;\;\;\; i=j \\
0, & \;\;\;\; i\neq j \\
\end{array}
\right.
$$
and write
$$
\inr{v_i}{v_j} \eql \delta_i(j)
$$
- Notice that the \(\delta_i(j)\) are also vectors:
- For example, \(\delta_3()\) is: (3rd element is \(1\))
$$
(0,0,1,0, \ldots, 0)
$$
- That is, only \(\delta_3(3)=1\). The rest are \(0\)s.
- If an operator \(A\) has an eigenbasis \(\kt{\phi_i}\) with
eigenvalues \(\lambda(i)\), then we
know two things:
- The action of \(A\) on its own eigenvectors:
$$
A \kt{\phi_i} \eql \lambda(i) \kt{\phi_i}
$$
- Any vector can be expressed in this eigenbasis:
$$
\kt{w} \eql \sum_i \alpha(i) \kt{\phi_i}
$$
With this (slightly changed) notation,
let's first look at countably infinite vectors:
- Here, a countably infinite vector has components labeled by
the integers:
$$
\kt{w} \eql \mat{c(1) \\ c(2) \\ \vdots \\ c(i) \\ \vdots }
$$
- And a basis will have a countably infinite collection of
vectors, where expressing in terms of such a basis looks like:
$$
\kt{w} \eql \sum_{i=1}^\infty c(i) \kt{v_i}
$$
- An operator is expressed as an infinite dimensional matrix
(both rows and columns):
$$
A\kt{w} \eql
\mat{
a_{11} & a_{12} & \ldots \\
a_{21} & a_{22} & \ldots \\
\vdots & \ddots & \ldots }
\mat{c(1) \\ c(2) \\ \vdots }
$$
- One problem we need to worry about: do sums converge?
- The theory is developed in a way to restrict attention
to vectors (and operators) where sums are convergent, as in
$$
\kt{w} \eql \sum_{i=1}^\infty c(i) \kt{v_i}
\; \lt \; \infty
$$
- With that restriction, just about everything we've seen
in finite discrete linear algebra applies.
- For example, standard basis vectors are
$$\eqb{
\kt{v_1} & \eql & (1, 0, 0, \ldots) \\
\kt{v_2} & \eql & (0, 1, 0, \ldots) \\
\kt{v_3} & \eql & (0, 0, 1, \ldots) \\
\vdots & & \\
}$$
- However, this type of infinity has found limited use.
- Variables of interest in modeling physical phenomena tend
to be real valued and therefore continuous.
11.7
Towards the continuum, part 2: what do we need from a continuous
linear algebra?
Let's examine a few core concepts from discrete linear algebra
and ask what they would look like in the continuous domain.
We'll state these in the form of puzzles to resolve:
- Puzzle #1: what do linear combinations look like?
- In the discrete case, we wrote
$$
\kt{w} \eql \sum_i c(i) \kt{v_i}
$$
- In the continuous case, we'd expect a sum to be replaced by
an integral, along the lines of
$$
\kt{w} \eql \int_x c(x) \kt{v_x} dx
$$
- However, what does it mean to integrate the vector \(\kt{v_x}\)?
- And what is a continuous vector \(\kt{v_x}\) anyway?
- What do its components look like?
- Puzzle #2: what do inner products look like?
- If we've solved the first puzzle and it's true that
$$\eqb{
\kt{w} & \eql & \int_x c(x) \kt{v_x} dx \\
\kt{u} & \eql & \int_x b(x) \kt{v_x} dx \\
}$$
then is
$$
\inr{w}{u}
\eql
\int_x c^*(x) b(x) dx
$$
analogous to the discrete case where
$$
\inr{w}{u} \eql
\sum_i c^*(i) b(i)?
$$
- Puzzle #3: What does orthonormality look like?
- We've described orthonormality as
$$
\inr{v_i}{v_j}
\eql
\left\{
\begin{array}{cc}
1, & \;\;\;\; i=j \\
0, & \;\;\;\; i\neq j \\
\end{array}
\right.
$$
in the discrete case.
- Is the continuous equivalent to the following,
$$
\inr{v_x}{v_y}
\eql
\left\{
\begin{array}{cc}
1, & \;\;\;\; x=y \\
0, & \;\;\;\; x\neq y \\
\end{array}
\right.
$$
where \(x,y\) are real numbers?
- Puzzle #4: How do probabilities emerge from coefficients, and how does
unit length play a role?
- For example, is
$$
\inr{w}{w} \eql \int_x c^*(x) c(x) dx \eql 1?
$$
- How does one calculate probabilities?
- Puzzle #5: What do operators and their eigen-stuff look like?
- Will we have the continuous equivalent
$$
A \kt{\phi_x} \eql \lambda(x) \kt{\phi_x}?
$$
- And will any vector be expressible in the continuous basis
\(\kt{\phi_x}\)?
- Puzzle #6: How do outer-products and projectors work
in the continuous case?
(And is measurement carried out with such projectors, if they exist?)
- Puzzle #7: How do tensor products work in the
continuous case?
11.8
Towards the continuum, part 3: some aspects of continuous linear algebra
We'll now examine how some of the above puzzles are resolved.
Before that, let's step back and recall the difference
between a vector and its numerical realization:
Now let's return to the continuous case:
- Analogous to the discrete case, we "numerify" a vector
with a continuous collection of coefficents \(c(x)\):
- Since \(x\) is real-valued, \(c(x)\) is just our familiar
function.
- Since coefficients are complex, the output of the
function is a complex number.
- Let's contrast with the discrete case:

- In this case:
- We'll have a set of basis vectors indexed by real numbers:
\(\kt{v_x}\).
- And coefficients \(c(x)\) such that a vector is expressed
in this basis using an integral.
$$
\kt{w} \eql \int_x c(x) \kt{v_x} dx
$$
- And an inner product for two "numerified" vectors is simply
$$
\inr{w}{u}
\eql
\int_x c^*(x) b(x) dx
$$
where \(\kt{w}\) is numerified by the function \(c(x)\)
and \(\kt{u}\) by \(b(x)\).
- When doing so, one scales by appropriate constants to
maintain unit-lengths.
Next, let's examine the connection between the coefficient function \(c(x)\)
and inner products:
- In the discrete case:
$$\eqb{
\inr{v_i}{w} & \eql & c(i) \\
& \eql & \sum_j \delta_i(j) c(j)
}$$
where
$$
\delta_i(j)
\eql
\left\{
\begin{array}{cc}
1, & \;\;\;\; i=j \\
0, & \;\;\;\; i\neq j \\
\end{array}
\right.
$$
are functions we defined to "pick off" the \(i\)-th coefficient.
- For example:
- Suppose we want to pick off \(c(2)\).
- Then
$$\eqb{
\delta_2(1) & \eql & 0 \\
\delta_2(2) & \eql & 1 \\
\delta_2(3) & \eql & 0 \\
}$$
so that
$$\eqb{
\delta_2(1) \cdot c(1) + \delta_2(2) \cdot c(2)
+ \delta_2(3) \cdot c(3)
& \eql & 0\cdot c(1) + 1 \cdot c(2) + 0\cdot c(3) \\
& \eql & c(2)
}$$
- Therefore, what's needed in the continuous case is an
equivalent \(\delta\) function with the property
$$
c(x) \eql \int_y \delta_x(y) c(y) dy
$$
where integrating the product \(\delta_x(y) c(y)\) picks off
\(c(x)\).
- For the moment, let's assume such a function exists:
- We don't really need to know what this function is.
- Just how it acts inside integrals like the one above.
- Here, it "picks off" the coefficient \(c(x)\) from the
continuum \(c(y)\) via the integral.
-
This is called the Dirac Delta function, which turns out
not to be a "function" in the usual sense:
- There are a variety of such "functions".
- Each is represented as a collection dependent on some
parameter that controls their "size" in the limit.
- For example:
$$
\delta_0^{(n)}(x) \eql \smf{n}{\sqrt{\pi}} e^{-n^2x^2}
$$
The integral of each is 1 but as \(n\to\infty\), the
shape approaches that of a "spike", as in
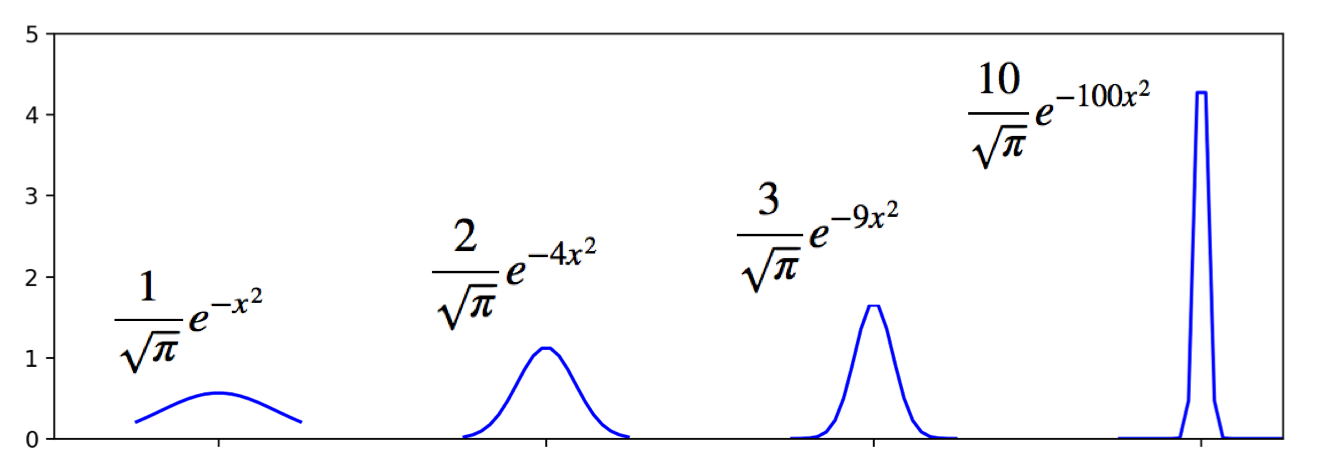
- We have written a generic such function as \(\delta_x(y)\)
where \(y\) is a variable and spike is centered at \(x\).
- It is often written as \(\delta(y-x)\).
- One implication of using this function:
- The inner products of basis vectors in the discrete case is:
$$
\inr{v_i}{v_j} \eql \delta_i(j)
$$
- For discrete vectors, \(\delta_i(j)\) is either \(0\) or \(1\).
- In the continuous case:
$$
\inr{v_x}{v_y} \eql \delta_x(y)
$$
- To see why this integral-use approach is needed,
suppose we were to define \(\delta_x(y) = 1\) only when
\(x=y\) and \(\delta_x(y) = 0\) otherwise:
- This is a function that has a spike of height \(1\) at \(x\).
- And it's \(0\) everywhere else.
- Unfortunately, this leads to a technical difficulty with
the "picking off" part:
$$\eqb{
c(x) & \eql & \int_y \delta_x(y) c(y) dy\\
& \eql & \int_{y\neq x} \delta_x(y) c(y) dy
\; + \; \int_{y=x} \delta_x(y) c(y) dy \\
& \eql & \int_{y\neq x} 0\cdot c(y) dy
\; + \; \int_{y=x} 1\cdot c(y) dy \\
& \eql & 0
}$$
- The technical difficulty can be resolved by introducing
a "generalized function" with certain properties, which we won't go
into here, to make the integral work, i.e., so that
$$
c(x) \eql \int_y \delta_x(y) c(y) dy
$$
- From our point of view, all we need to know is how
to apply \(\delta_x(y)\) inside an integral.
Before tackling operators, let's simplify notation:
- We've used \(c(x)\) to numerify a continuous vector \(\kt{w}\).
- Instead of using two symbols, we'll simply write
$$
\kt{w} \eql \kt{c(x)}
$$
and dispense with the former.
- Thus, if \(\psi(x)\) is a function that represents
coefficients, then the corresponding vector is \(\kt{\psi(x)}\).
Let's now review what we have so far:
- Puzzle #1: what do linear combinations look like?
We do in fact have
$$
\kt{w} \eql \int_x c(x) \kt{v_x} dx
$$
- Puzzle #2: what do inner products look like?
As anticipated, we have
$$
\inr{w}{u}
\eql
\int_x c^*(x) b(x) dx
$$
with the appropriate scaling (normalization) to maintain unit-length.
- Puzzle #3: What does orthonormality look like?
We now have this all-purpose Delta "function" that let's us define
$$
\inr{v_x}{v_y} \eql \delta_x(y)
$$
- Puzzle #4: How do probabilities emerge from coefficients?
- In the discrete case, the squared-magnitude of a coefficient
gave us the probability associated with the corresponding eigenvector.
- For example, if we expressed a vector in terms of
a measurement eigenbasis
$$
\ksi \eql \sum_i \alpha(i) \kt{\phi_i}
$$
then the probability of seeing \(\kt{\phi_i}\) is
\(\magsq{\alpha(i)} = \alpha^*(i)\alpha(i)\).
- If in the continuous case, the coefficient function
when expressing \(\ksi\) in terms of an eigenbasis is
$$
\ksi \eql \int_x \alpha(x) \kt{\phi(x)} dx
$$
then the probabilities arise through
$$
\mbox{Pr[observe outcome in \([\phi(x), \phi(x+\epsilon)]\)]}
\eql
\int_x^{x+\epsilon} \alpha^*(y) \alpha(y) dy
$$
- That is, via integrating the probability density function
implied by the eigenbasis.
- Appropriate normalization is introduced so that
$$
\int_y \alpha^*(y) \alpha(y) dy \eql 1
$$
Before examining operators, let's ask:
what continuous basis should we use for calculations?
- In the discrete case, it did not matter much:
- For example, in the Stern-Gerlach experiment, a z-aligned
apparatus uses the standard-basis.
- This makes the x-aligned apparatus the H-basis.
- But we could also use the S-basis for x-aligned, and
H-basis for vertical.
- The other aspect of linear algebra that did not matter was:
eigenvalues:
- We did not use this for quantum computing because we focused
only on the states that were measurement outcomes.
- But an actual experimental measurement also produces an eigenvalue.
- In fact, the eigenvalue is the actual physically observable quantity.
- In the continuous case, actual physical observables do
matter both in theory and in practice.
- The most intuitively fundamental physical observable is location:
where in 3D space, an object is.
- In one dimension (to simplify), this is an x-value (along
the x-axis).
- Thus, if a real number like \(x\) is an observed eigenvalue,
what are the corresponding eigenvectors and operator?
- Suppose we could find an operator \(A_{pos}\) (for position)
and eigenvectors \(\kt{\phi_x}\) so that
$$
A_{pos} \kt{\phi_x} \eql x \kt{\phi_x}
$$
- Then, the observed position \(x\) is the result
(eigenvalue) of a
position measurement, with resulting state \(\kt{\phi_x}\).
- This should immediately raise a question:
- Don't measurements result in probabilistic outcomes?
- If so, does that mean the position of a quantum object
is necessarily probabilistic, according to the theory?
- This set of eigenvectors \(\kt{\phi_x}\) is the
default starting basis called the position basis.
- What do the eigenvectors \(\kt{\phi_x}\) look like?
Do they look like the all-zeroes-but-one-1 eigenvectors
we've seen in the discrete case?
- The reasoning is a bit tricky:
- We've already seen that we can't have spike=\(1\) functions.
- Consider two x-values \(x\) and \(x^\prime\).
- Then, in the integral
$$
\int_y \delta_{x^\prime}(y) \delta_x(y) dy
$$
the first delta-function picks off the value \(x^\prime\) in the
second, so
$$
\int_y \delta_{x^\prime}(y) \delta_x(y) dy
\eql
\delta_x(x^\prime)
$$
- But, by our definition of inner-products for orthonormal
vectors,
$$
\inr{\phi_x}{\phi_{x^\prime}} \eql \delta_x(x^\prime)
$$
Thus, the integral above (on the left) is in fact the inner
product \(\inr{\phi_x}{\phi_{x^\prime}}\).
- Which means the two functions in the integral are in fact
the functions that define the eigenvectors:
$$\eqb{
\phi_x(y) & \eql & \delta_x(y) & \mbx{eigenvector for \(x\)}\\
\phi_{x^\prime}(y) & \eql & \delta_{x^\prime}(y) &
\mbx{eigenvector for \(x^\prime\)}\\
}$$
- Thus, when the position eigenbasis is represented in
its own basis, the corresponding coefficient functions
are delta-functions.
- If this all seems rather complicated, that's because it is!
- None of this was fully worked out until Paul Dirac put the pieces
together.
- And, as it turns out, Dirac's version was not mathematically
rigorous.
- The formal rigorous underpinning would take years to address.
- Finally, let's simplify notation once more:
- We've used the continuous position
basis \(\kt{\phi_x}\) indexed by position \(x\).
- Again, instead of two symbols, one directly writes
the \(\kt{x}\) as a basis vector.
- Then,
$$
A_{pos} \kt{x} \eql x \kt{x}
$$
which at first is a bit confusing and takes some getting used to.
- With this simplification, we can write
$$
\inr{x}{\psi} \eql \int_y \delta_x^*(y) \psi(y) dy \eql \psi(x)
$$
where the vector \(\psi(y)\) is the "numerification" of
\(\kt{\psi}\) in the position basis.
- This has a nice interpretation:
- Recall that \(\inr{v}{w}\) is the coefficient of \(\kt{w}\)
along \(\kt{v}\).
- Then, in \( \inr{x}{\psi}\) we get the coefficient of
\(\kt{\psi}\) along the x-axis, which is simply \(\psi(x)\).
- And where did this \(\psi(x)\) come from?
- We will see that \(\psi(x)\) is determined by Schrodinger's
equation that, in some sense, describes the "physics" of the
object of interest.
- Because we have unit-lengths, we will normalize to enforce
$$
\int_x \psi^*(x) \psi(x) dx \eql 1
$$
- Which makes \(\psi^*(x) \psi(x) = \magsq{\psi(x)}\) a probability density function,
from which we can calculate
$$
\mbox{Pr[observe position in \([a, b]\)]}
\eql
\int_a^b \magsq{\psi(x)} dx
$$
- Let's summarize:
- The preferred starting point is the position basis, whose
vectors are denoted by \(\kt{x}\), one for each value of
possible locations \(x\).
- The actual observed eigenvalues are the locations \(x\).
- This means a measurement Hermitian \(A_{pos}\) must have
\(\kt{x}\) as eigenvectors and \(x\) as eigenvalues:
$$
A_{pos} \kt{x} \eql x \kt{x}
$$
- The eigenvectors \(\kt{x}\) when numerified turn out
to be the delta functions \(\delta_x(y)\).
Next, let's look at operators in general:
- We need to address several questions at the very least:
- What is an operator in the continuous case and
how does one "numerify" it? That is, how does one
calculate
$$
A \kt{\psi(x)} \eql ?
$$
for an operator \(A\)?
- How does one determine the coefficients in expressing a
vector in this eigenbasis
$$
\kt{\psi(x)} \eql \int_{y} \alpha(y) \kt{\phi_y(x)} dy?
$$
- What kinds of operators are useful?
- Let's start with what an operator does:
- When numerified, a vector \(\kt{\psi(x)}\) is a function \(\psi(x)\).
- Thus, when numerified, an operator is something that acts
on a function to produce a function.
- What kinds of operators do this?
- There are many, but certainly differentiation is one of them:
$$
\frac{d}{dx} \psi(x) \eql g(x) \;\;\;\;\; \mbox{\(g(x)\) is
some function}
$$
where \(\frac{d}{dx}\) is an operator.
- Just like the H-basis was the second important qubit basis,
in the continuous vector world, the second important basis
is the momentum basis.
- A particle's position describes current location.
- Momentum describes its current motion.
- Again, momentum is a physically observable real number:
let's call this \(p\):
- Which means there is some Hermitian \(A_{mo}\) operator such that
for any momentum eigenstate \(\kt{p}\):
$$
A_{mo} \kt{p} \eql p \kt{p}
$$
- The question of course is: what are these momentum eigenstates
when written in the position basis, and what is the operator?
- Relatedly: can position be described in the momentum basis?
- Without getting into the technical details, we'll state
that each momentum eigenstate numerified (in the position basis)
works out to the function
$$
\kt{p} \eql \smf{1}{\sqrt{2\pi}} e^{\frac{ipx}{\hbar}}
$$
- We can now ask the question: suppose we have some
generic state \(\kt{\psi(x)}\) in the x-basis, what
does this look like in the momentum basis?
- Let \(\tilde{\psi}(p)\) denote the coefficient function
(of \(p\)) of the same state in the momentum basis.
- Then one can show that
$$\eqb{
\tilde{\psi}(p) & \eql &
\smf{1}{\sqrt{2\pi}} \int e^{\frac{-ipx}{\hbar}} \, \psi(x) \, dx\\
\psi(x) & \eql &
\smf{1}{\sqrt{2\pi}} \int e^{\frac{ipx}{\hbar}} \, \tilde{\psi}(p) \, dp\\
}$$
- This allows going to-and-from one basis to another.
- Notice: the calculation involves doing something to one
function to produce the other.
- This pair of actions is together called the Fourier transform,
the second of the three Fouriers.
- The third: the Discrete Fourier Transform (DFT), that
we saw in Shor's Algorithm.
- Lastly, we should ask: where did the exponentials come from?
- The momentum operator turns out to be the differential
operator \(-i\hbar \frac{d}{dx}\).
- When applied to the eigenvector-eigenvalue equation, that
equation becomes a differential equation whose solution is exponential.
Other puzzles we haven't resolved but won't have time for:
- Outer products and projectors.
- Tensor products.
The fact that momentum is involved suggests that something is "moving"
or changing with time:
- If the state is changing with time, we need an additional
variable for time.
- Let
$$\eqb{
\kt{\psi(x,0)} & \eql & \mbox{state at time 0} \\
\kt{\psi(x,t)} & \eql & \mbox{state at time t} \\
}$$
- Now, what used to be the coefficient function \(\psi(x)\) has an
additional variable \(t\) to denote time: \(\psi(x,t)\)
- This raises the question: what determines how the state
changes with \(t\)?
11.9
Towards the continuum, part 4: postulates of quantum mechanics
About postulates:
-
They're called postulates because there is no underlying
theory from which these postulates can be derived.
- In some sense, they are assumptions from which
the rest of the theory is developed.
- Interestingly, there is a bit of divergence amongst
physicists in how best to state the postulates.
- Now, one can describe the postulates with or
without relativity.
\(\rhd\)
We will describe the (simpler) non-relativistic postulates.
- Another issue is whether the system under consideration is
isolated from external influences.
\(\rhd\)
We'll assume isolation.
- We'll state them for the one-dimensional case
and then comment.
The (non-relativistic) postulates of quantum mechanics:
- State description postulate. The state of an isolated
quantum-mechanical system is described by a continuous complex vector
\(\kt{\psi(x,t)}\).
- Measurement postulate. Every physical measurement is described
by a Hermitian operator \(M\) such that:
- The eigenvectors of \(M\) are the outcome states of measurement.
- The (real) eigenvalues of \(M\) are the physically observed quantities.
- For any state \(\kt{\psi(x,t)}\) and outcome
eigenvector \(\kt{\phi(x)}\), the probability of observing
that outcome is proportional to \(\magsq{\inr{\phi(x)}{\psi(x,t)}}\).
- State change postulate. The
dependence on time is prescribed by the Schrodinger equation
$$
i\hbar \frac{\partial}{\partial t} \kt{\psi(x,t)} \eql H(t) \kt{\psi(x,t)}
$$
where \(H(t)\) is an operator, potentially itself time-varying,
called the quantum Hamiltonian operator
constructed in a particular way:
- Classical quantities like position \(x\) and momentum \(p\)
are replaced by corresponding quantum operators like
\(A_{pos}\) and \(A_{mo}\) to form \(H\).
Now let's point out a few things:
- We've only stated the postulates in the simplest possible way,
for one dimension, without relativity, and for a confined system.
- The state description should be somewhat familiar to us,
except for the dependence on time.
- The Schrodinger equation is entirely new, about which we'll
say more below.
- The coefficient function \(\kt{\phi(x,t)}\) is often called
the wavefunction.
- Some books include tensoring as a postulate, others
state that it's a consequence of the statistical independence of
subsystems (and is not needed as a postulate).
Schrodinger's equation and unitary evolution:
- First, observe: it's a differential equation.
- One might wonder: is it derived from something more
elementary, like many other differential equations
in science and engineering.
- The answer: no, there is no underlying principle that leads
to this equation.
- Second, a state that's changing according to the equation
is changing unitarily:
- When \(H(t) = H\) (not varying with time), one can show
that
$$
\kt{\phi(x,t)} \eql U(t) \kt{\phi(x,0)}
$$
where
$$
U(t) \eql e^{-iHt/\hbar}
$$
is a unitary operator.
- Thus, the state is changing as if a unitary operator
is being applied.
- A similar but more technical argument shows that the
state changes unitarily even if \(H(t)\) varies with time.
Let's focus on an important takeaway:
- The two key phases of a quantum system carry over into
the continuous domain:
- The system evolves unitarily until a measurement is made.
- A measurement drastically and probabilistically
alters the state into one of the measurement's eigenstates.
- But what is the nature of
this drastic change and how does it happen?
- For example:
- When a polarized photon goes through a filter, what exactly
causes the drastic change in polarization?
- When a Stern-Gerlach atom travels through the apparatus
in superposition, and one sees two separated landing spots,
where does the measurement occur?
- Another example:
- When an electron goes through the double slit, it does so
in superposition, and yet lands in one single spot.
- The wavefunction shows some spread and yet it collapses to
one single location.
- And why is measurement probabilistic?
- These two issues, collapse and non-determinism,
together constitute the biggest unresolved mystery
in quantum mechanics: the measurement problem.
11.10
Schrodinger's cat
Let's return to the famous double-slit experiment:
- Recall the interference pattern:
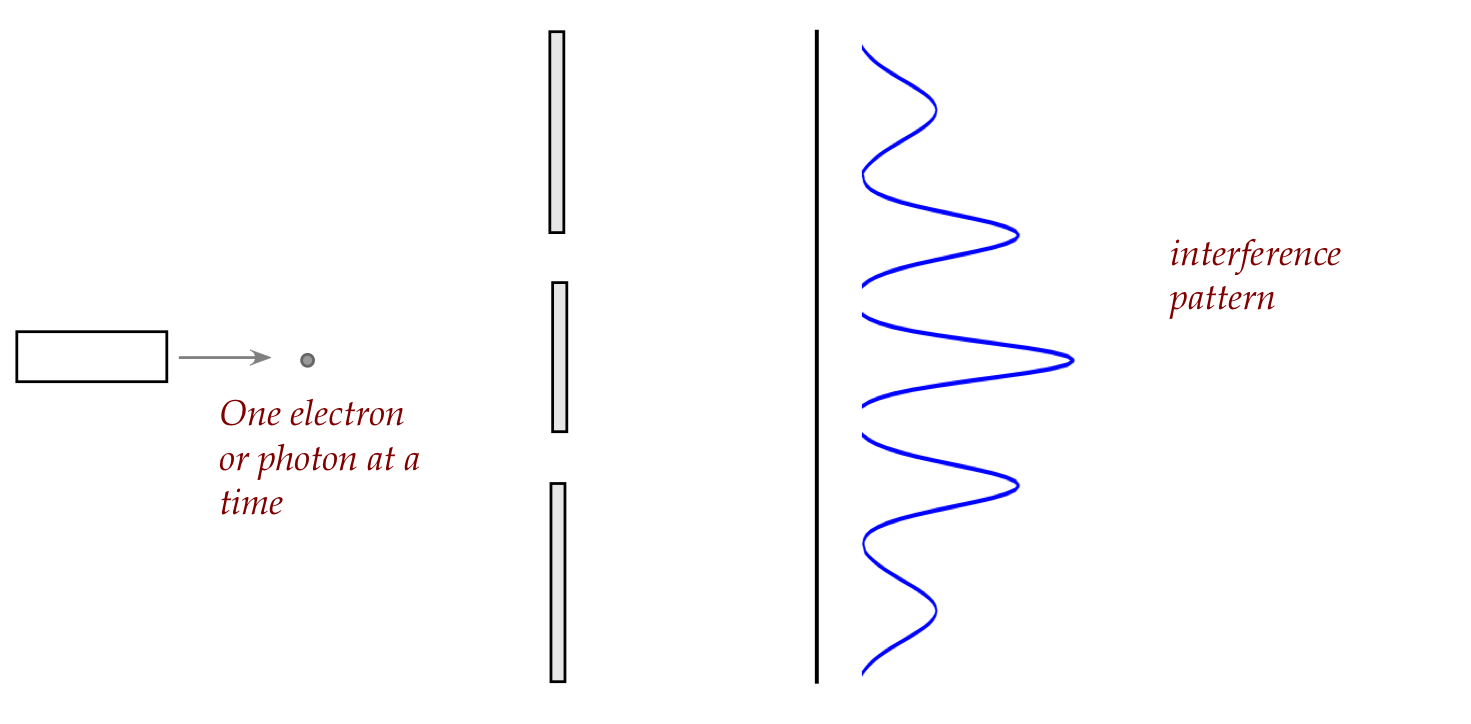
- The pattern is in fact the probability distribution (think:
continuous histogram) of where a single particle (photon or
electron) may land:
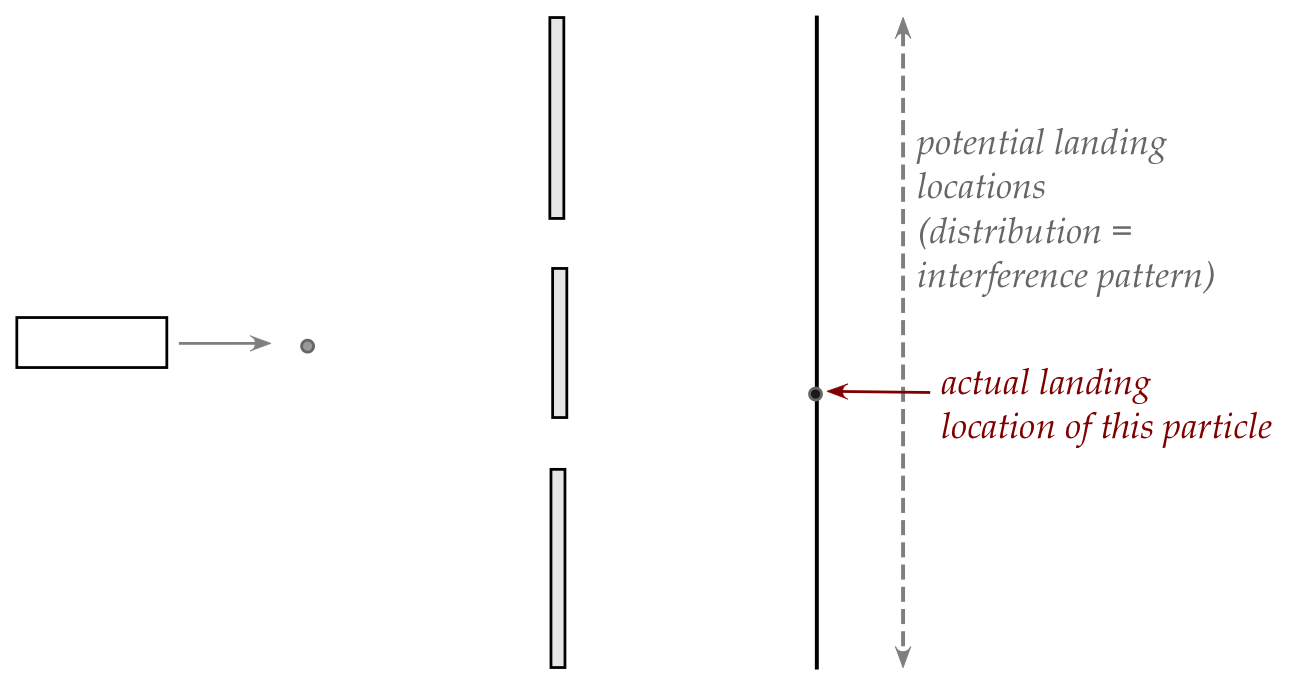
- What's important to note:
- The entirety of the photon or electron lands in one location.
- There is no splitting of such a particle.
- Let's measure landing location from the bottom of the screen:
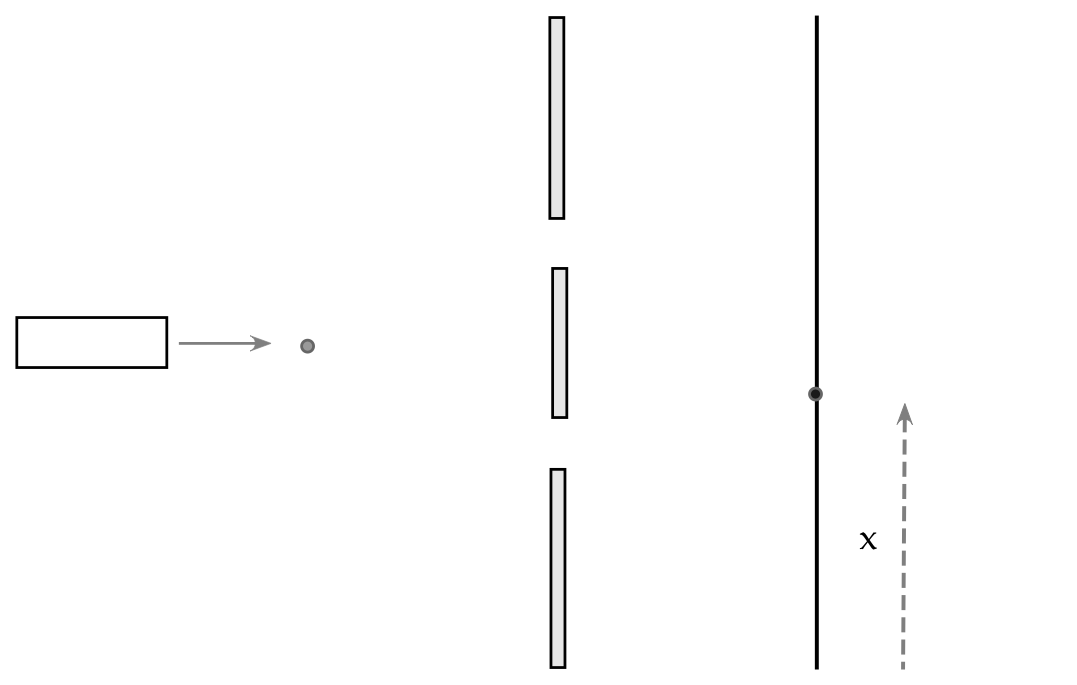
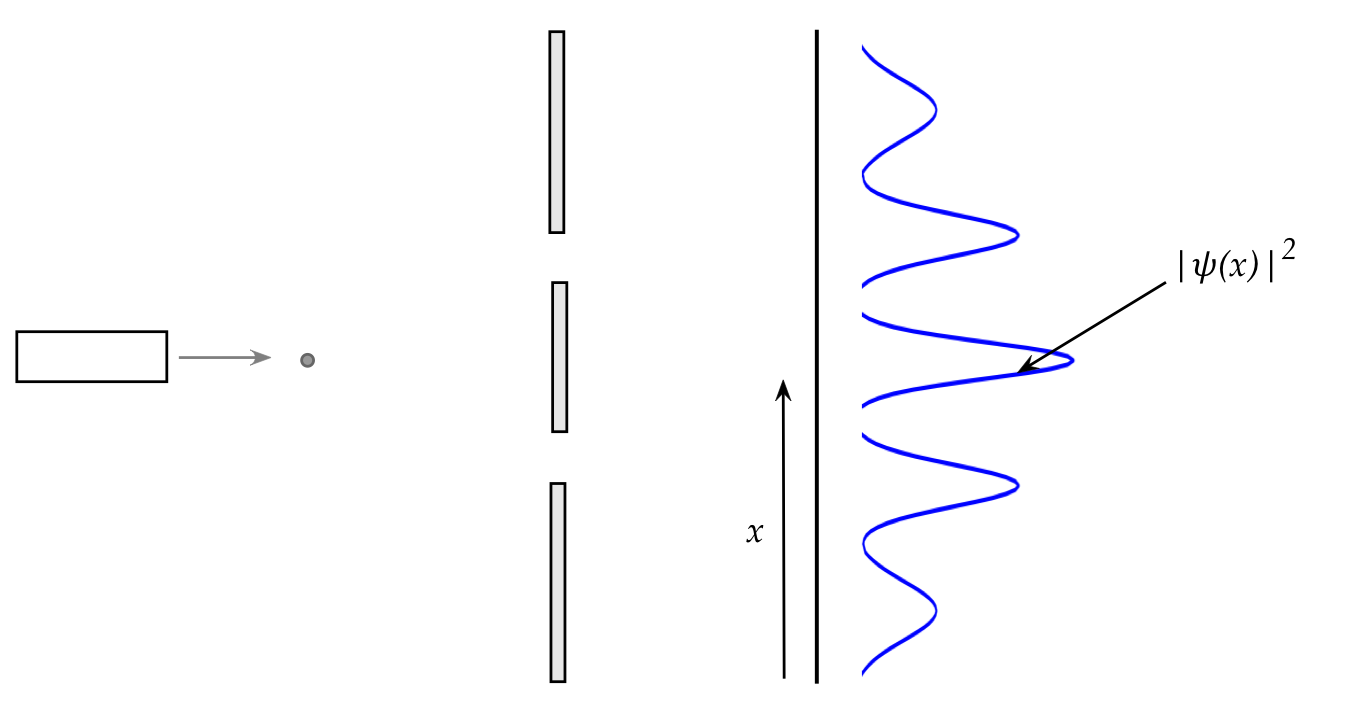
- Let's rephrase this as:
- Some wavefunction \(\kt{\phi(x)}\)
describes the probability of finding the
particle at location \(x\):
- A measurement (landing on the screen) results in a
particular position eigenvalue outcome \(x\).
- One could say that the wavefunction collapses
upon measurement.
- Another way to describe this:
- The quantum object (photon or electron) behaves like a
(probabilistic) wave before measurement.
- Then, it abruptly behaves like a particle.
This is sometimes called wave-particle duality.
Next, let's examine why this is a problem in quantum mechanics:
The Copenhagen diktat:
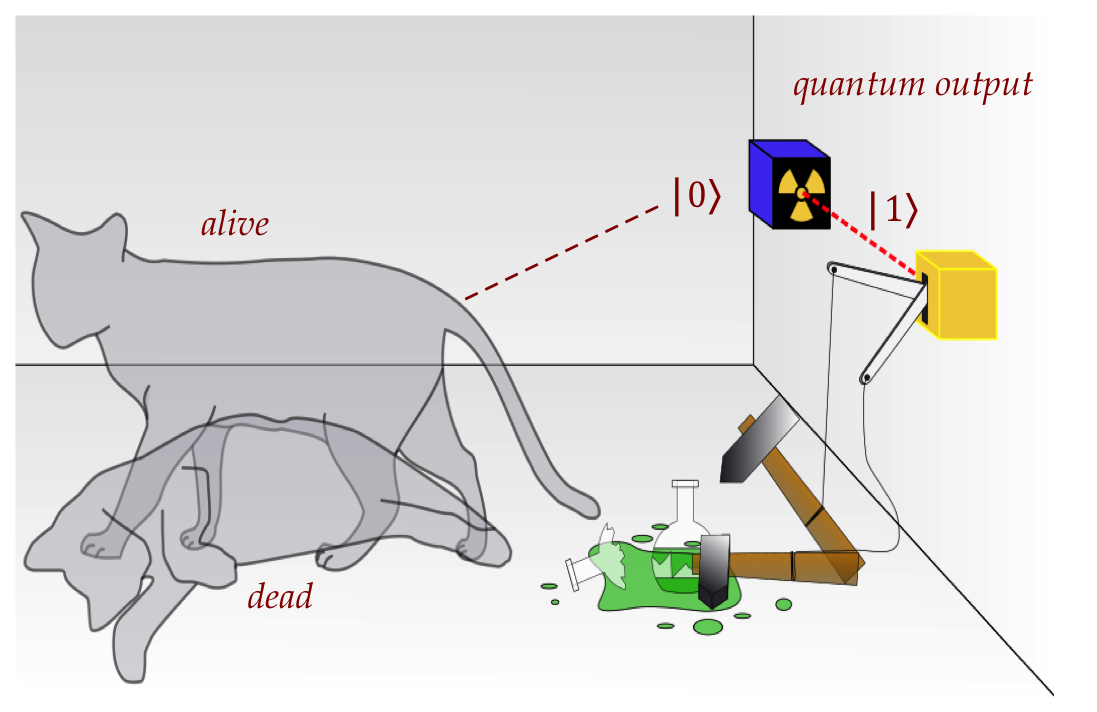
- To resolve the conundrum, physicist Niels Bohr and others said
the following:
- There is a sharp unknowable boundary between unitary
evolution and measurement.
(Equivalently, between wave and particle behavior.)
- When measurement occurs, the unitarily-evolving wavefunction
instantaneously "collapses" to a single point.
- Knowing the boundary is not needed for calculations and predictions.
- It is futile to delve into the measurement conundrum, so it's
best to ignore it.
- In some sense, this was a "don't ask, don't tell" rule.
- For years, nobody questioned this rule.
- This has come to be called the Copenhagen interpretation.
But Schrodinger and Einstein did not like this state of affairs:
Ideas about resolving the measurement conundrum are
typically called interpretations.
Let's look at a few of these next.
11.11
Interpretations
We have seen the Copenhagen interpretation.
We'll now briefly describe two historically important
ones: Pilot-Wave, and Many-Worlds.
And mention a few others.
The De-Broglie-Bohm pilot wave theory:
- Often credited to David Bohm, a former student of Oppenheimer in 1951.
- It turns out that a version of the theory had been proposed
earlier by Louis de Broglie.
- They differ slightly in the details.
- Both theories involve a global hidden variable called
a pilot wave.
- The main ideas:
- Every quantum object has an associated pilot wave that guides
its behavior.
- When particles interact, they have a joint pilot wave
in so-called configuration space.
- This wave extends throughout space and evolves through
Schrodinger's equation.
- The quantum object is a particle whose motion is guided by
the pilot wave.
Thus, every particle is both a wave and a particle, with the wave
directing the particle's motion.
- Bohm and De-Broglie
showed that their versions produce the same quantitative
results as QM-with-Copenhagen.
\(\rhd\)
On this, there's agreement amongst physicists.
- In pilot-wave theory,
randomness is explained via a dependence on initial particle
properties.
- What pilot-wave says about the double-slit:
- A particle goes through only one slit.
- The pilot wave, which does go through both slits,
determines which slit.
- What Bohm says about Schrodinger's cat:
- The cat will be in only one of the two states.
\(\rhd\)
There is no entangled state.
- The pilot wave of all involved particles determines which state.
- But Bohm's theory has also been criticized:
- There's no evidence of this mysterious pilot wave.
- To make the theory work, one has to believe that the pilot
wave for a single particle extends across the whole universe.
- There is no explanation of how the initial particle
properties arise.
- The theory uses location as the primary variable, with all
others secondary.
- This is an area of active research (and debate):
- When particles interact, it's only the waves that interact,
according to the theory.
Many Worlds:
- Developed by Hugh Everett, a student of QM pioneer John Wheeler.
- The main, and rather radical, idea:
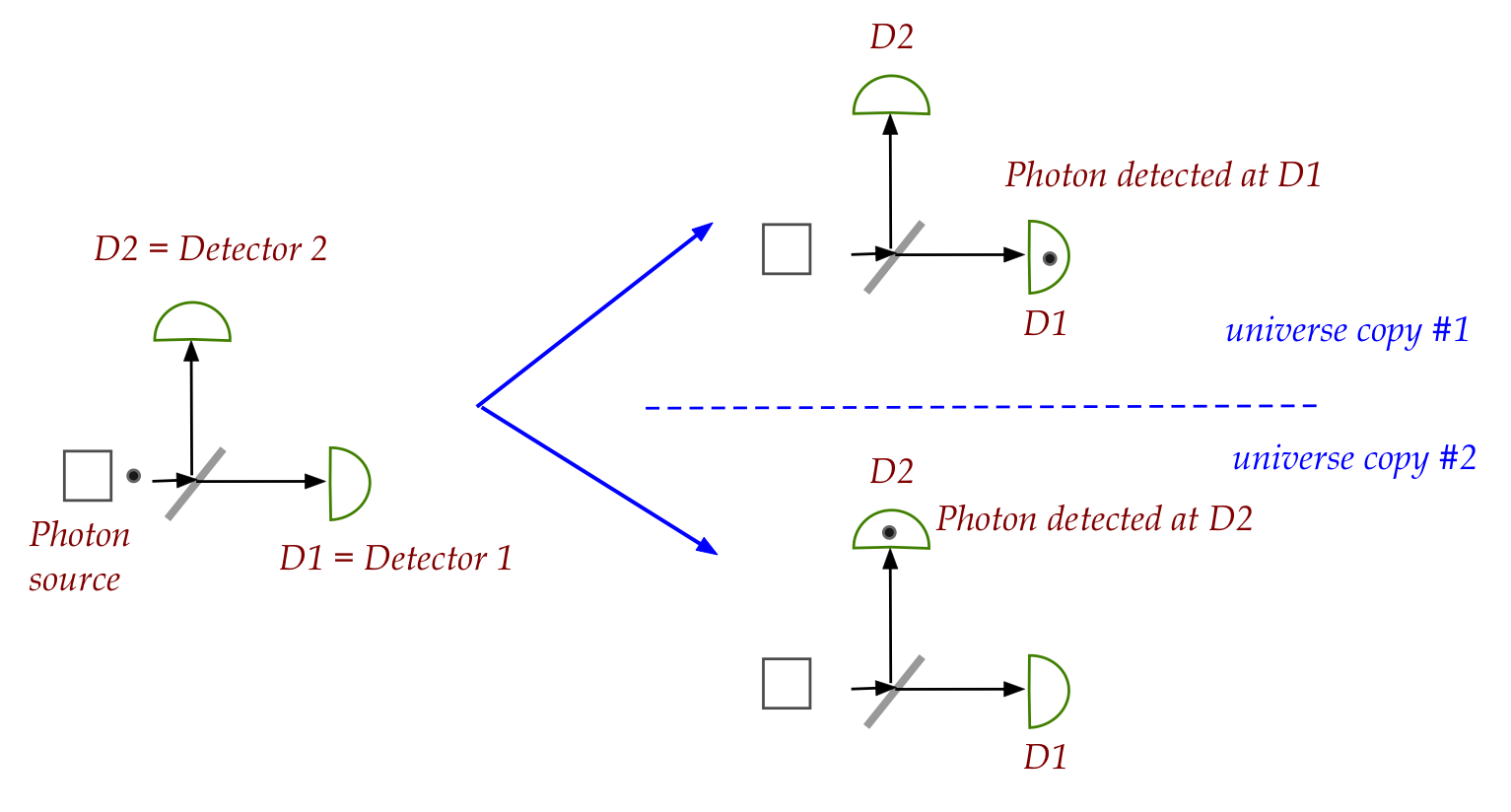
- Whenever measurement occurs for any particle, the universe
splits into multiple copies, one for each possible outcome.
- Thus, there is one universe in which Schrodinger's cat is
alive, and one in which its dead.
- The copies are identical in every other respect except for
the outcomes.
- What the theory hopes to do:
- Provide the simplest, most elegant explanation of measurement.
- Remove the non-determinism altogether.
In-Class Exercise 5:
What are your thoughts about the many-worlds idea?
There are now a host of theories, in various stages of
debate, acceptance, and experimentation, such as:
- Super-determinism:
- We used an independence assumption (between identical
photons) in showing hidden-variable theory was wrong.
- However, one can argue that photons carry hidden variables
that are correlated with the measuring device's hidden variables.
- These can be adjusted to produce the same predictions as
quantum theory.
- These variables get "set" at creation: the big bang.
- Like many-worlds, it's un-testable.
- Penrose's gravitation model:
- Gravitational effects play a role in determining a
measurement outcome, addressing why collapse occurs and where.
- The GRW theory:
- Named after authors Ghirardi, Rimini and Weber.
- It tweaks Schrodinger's equation to add a variable that
determines collapse.
- In the above two, the wave function collapse is non-instantaneous,
and based on physical principles.
11.12
Delayed choice and quantum eraser
We'll end this QM teaser by describing two intruiging
experiments.
Recall, the Mach-Zehnder set up that showed interference:
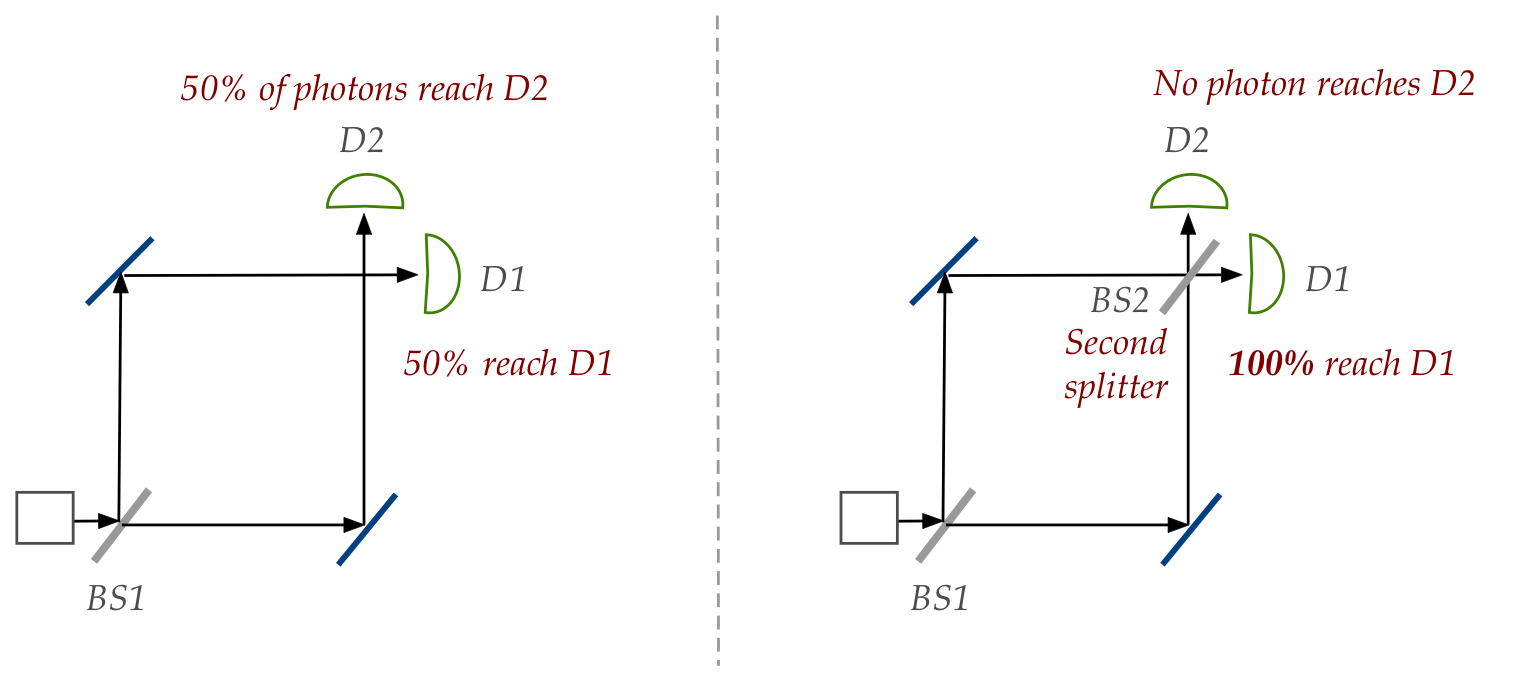
- Consider a single photon released from the source.
- In the first scenario, on the left, a photon has a 0.5
probability to take either path.
- In the second scenario, there is interference, and
no photon ever arrives at D2.
- Let's first examine the second case:
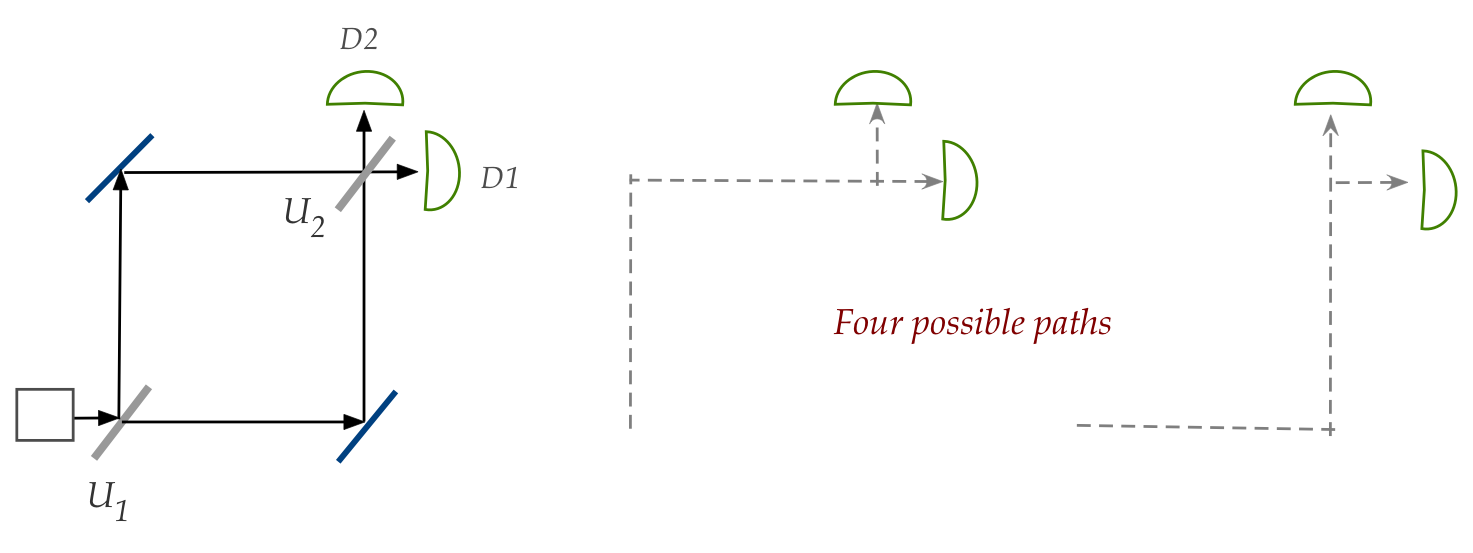
- Each splitter is a unitary operation on the photon's
wavefunction.
- The resulting wavefunction is a superposition of the
four possible paths.
- The coefficients of the paths to D2 add up to \(0\) because of the
careful set up with distances.
- The first scenario is just as interesting:
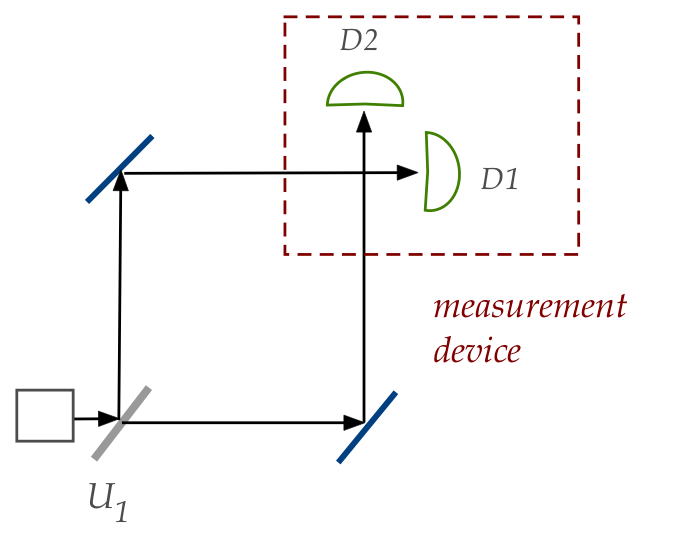
- The two detectors together act as a measurement device.
- Only one of them goes off, probabilistically.
- A skeptic might ask: doesn't the photon go one way or
the other at the first beam splitter in Scenario 1?
The delayed choice experiment:
- In this experiment, the second splitter can be
inserted after the photon has left the first,
and before it reaches the detector:
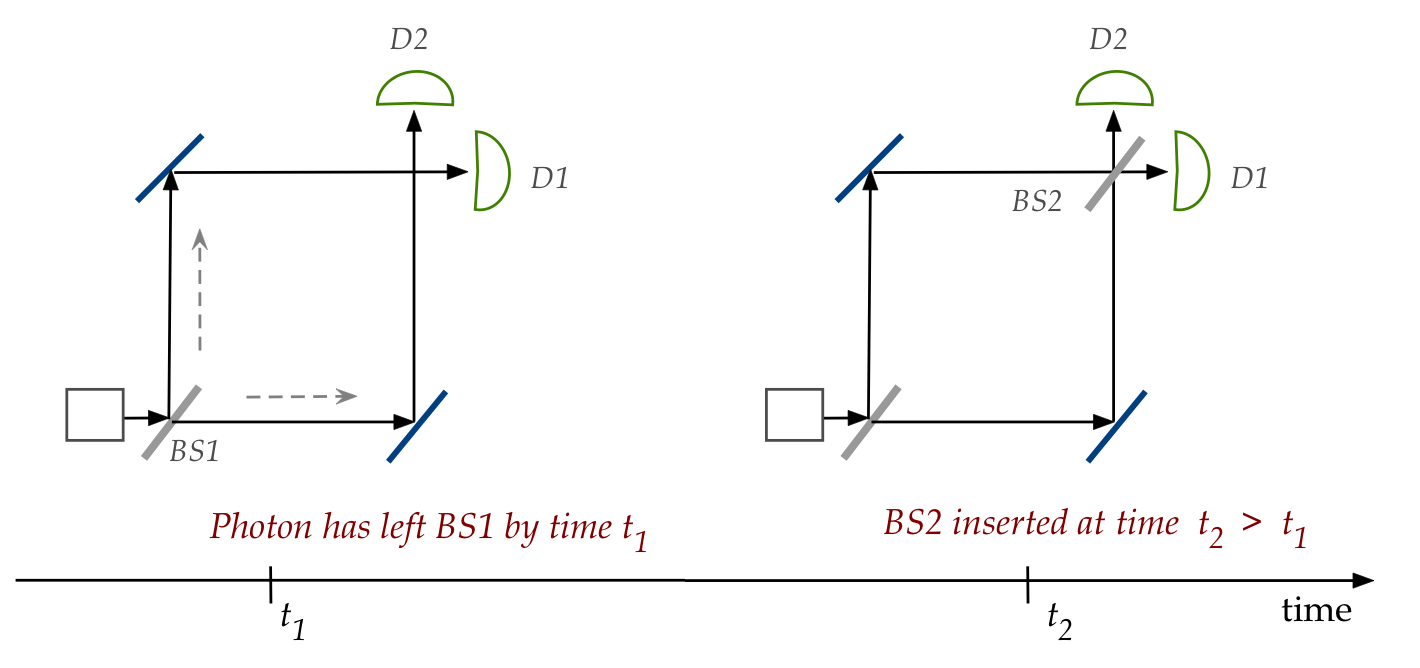
- For this set up, the paths have to be long enough to allow
for electronic insertion of the second splitter
- What is observed?
- Photons for which BS2 is not inserted
behave like Scenario 1: randomly landing on either D1 or D2.
\(\rhd\)
50% land on D2.
- Photons for which BS2 is inserted all go to D1.
\(\rhd\)
Interference is observed.
- What to make of this?
- The results are consistent with QM.
- But it forces us to acknowledge that the wavefunction is a
strange entity that spreads out (both BS1 paths).
- And that a unitary applied later (BS2) has immediate effect.
Finally, let's look at an even stranger result,
the quantum eraser experiment:
- First, consider the following set up:
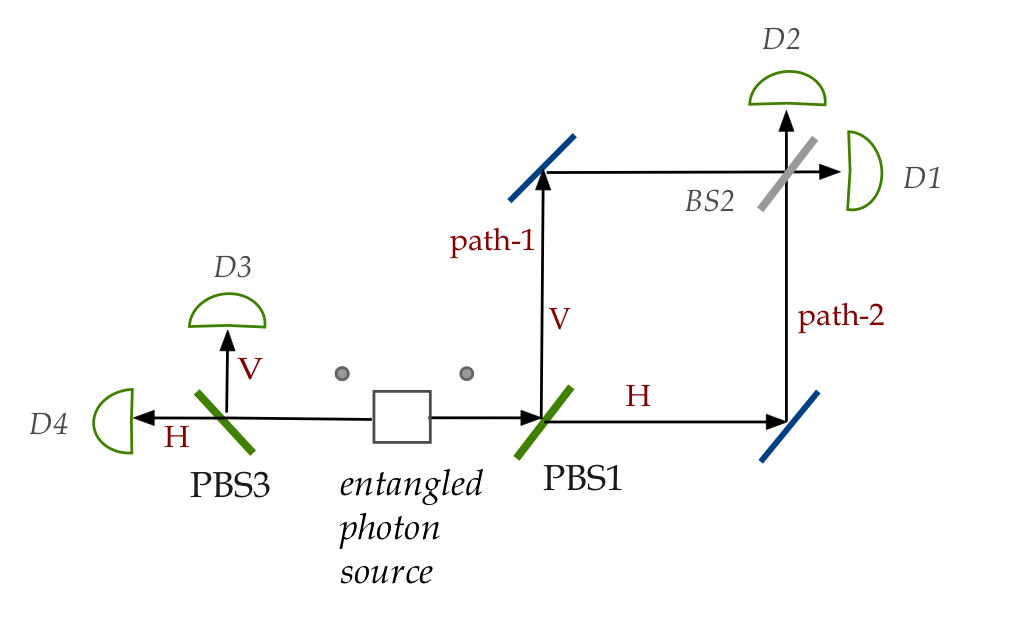
- A Polarizing Beam Splitter (PBS) will send horizontally and
vertically polarized photons in different directions.
- A source of entangled photons produces
polarization-entangled photons with state
$$
\ksi \eql \isqts{1} \parenl{ \kt{V}\kt{V} + \kt{H}\kt{H} }
$$
- Thus, if the left photon is detected at D3, then we know the
right photon takes path-1 in the figure.
\(\rhd\)
Thus, measuring the left photon provides which-path information.
- What QM predicts: when which-path is knowable, no
interference occurs.
- Thus, in the above case, even if we don't actually use the
left-side measurements, there will be no interference.
\(\rhd\)
50% at D1, 50% at D2
- In the next set up, the left photon's polarization is
scrambled randomly (perhaps by measuring in the \(45^\circ\) basis):
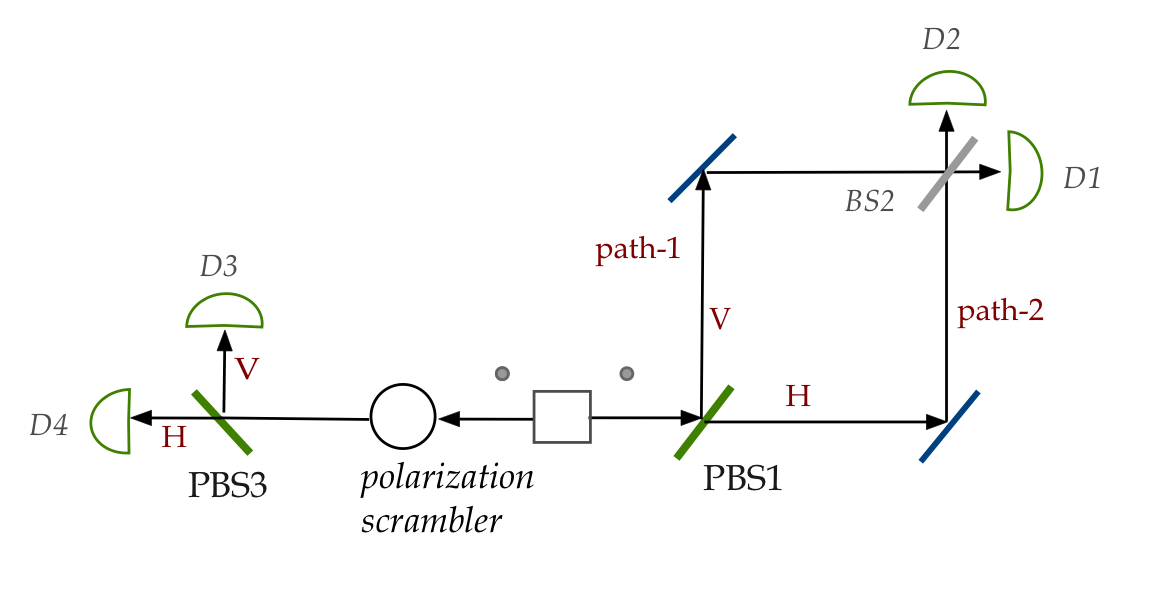
What this means:
- A \(45^\circ\)-polarized photon will have equal chance of
going up or straight on the left side.
- Thus, the left-side measurement reveals nothing about the path
taken on the right.
- What is observed in this case?
\(\rhd\)
Interference!
- But this interference is a bit subtle:
- Overall, there are still 50% at D1, 50% at D2.
- But if one separates out the photons on the right,
whose left-partners went to D3, then those photons will
show an interference pattern (100% of them at D1).
- Similarly, the others will show the opposite
interference pattern (100%
of them at D2).
- Now for the next set up:
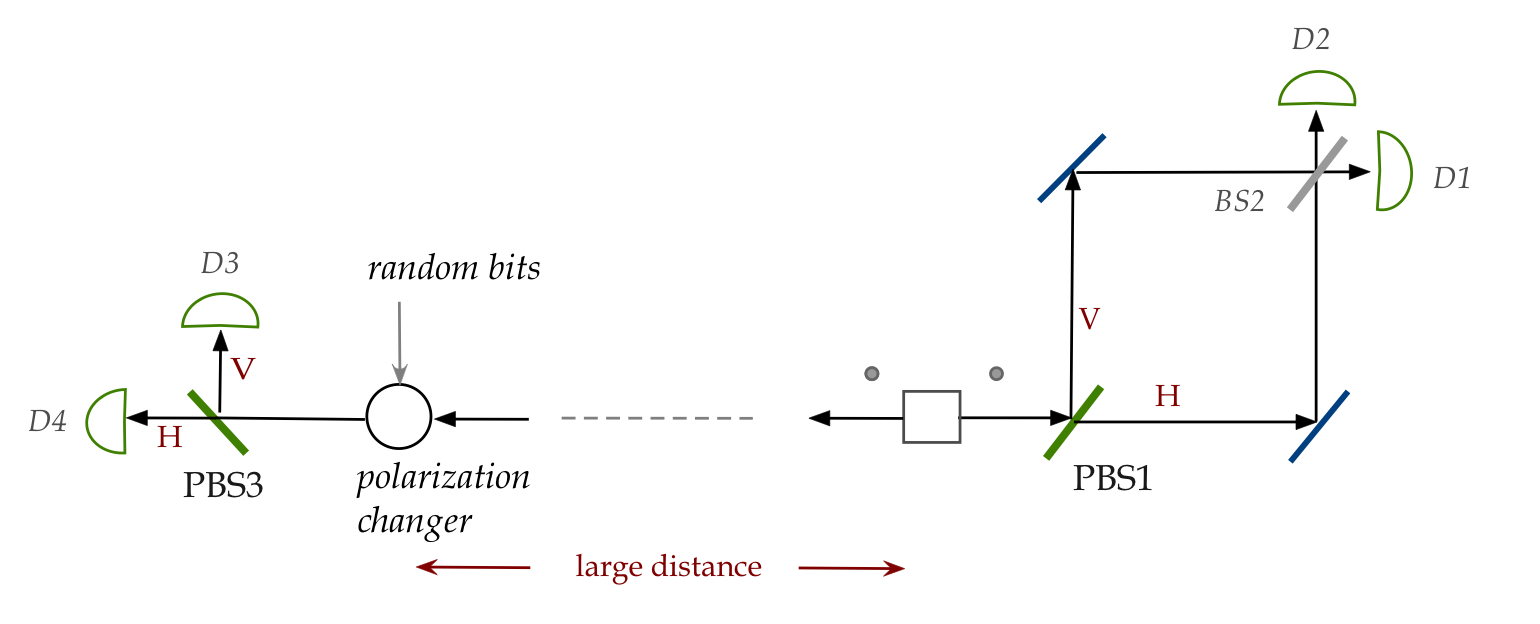
Here:
- A random generator turns on-and-off the polarization scrambler.
- A significant distance is introduced between the two parts so
that left photons reach the scrambler long after the right photons
have reached either D1 or D2.
- Note: the decision about whether to scramble or not occurs
after the right side measurement.
- What is observed?
- When left photons are scrambled, the right side equivalents
show interference.
- For the unscrambled left photons, the equivalent right side
ones do not exhibit interference.
- The term retrocausality has been used to label this
type of phenomenon.
With that, we will conclude our quick peek at quantum mechanics.