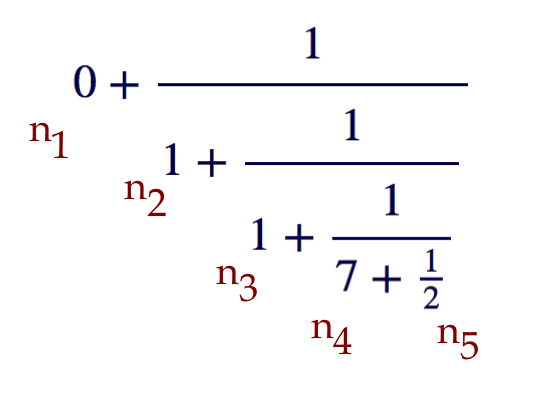Overview
Highlights of this appendix:
- The main focus: integers and operators that result in integers.
- But also, rational numbers and continued fractions like
$$
1 + \cfrac1{ 1 + \cfrac1{ 1 + \cfrac1{ 1 + \cfrac1{ 1 +
\frac{1}{2}} } } }
$$
- The idea of "mod-ing"
$$
a \md M \eql \mbox{remainder when \(a\) is divided by \(M\)}
$$
which goes hand-in-hand with "div"
$$
a \mbox{ div } M \eql \mbox{quotient when \(a\) is divided by \(M\)}
$$
- Example: \(13 \md 3 = 1\)
- Example: \(13 \mbox{ div } 3 = 4\)
- Using "mod" and "div" keeps the results integers.
- Curiously, we'll often be more interested in the remainder than
in the quotient.
- Greatest common divisor (gcd) and Euclid's algorithm:
- The gcd of \(a,b\) is the largest positive integer that
divides both \(a\) and \(b\).
\(\rhd\)
Example: \(\gcd(84,30)=6\) even though \(84\) and \(30\) share
other factors.
- One way to think of gcd is to write out the prime factorization:
$$\eqb{
84 & \eql & {\bf 2} \times 2 \times {\bf 3} \times 7\\
30 & \eql & {\bf 2} \times {\bf 3} \times 5 \\
}$$
where the common prime factors multiply
to give the gcd: \({\bf 2} \times {\bf 3} = 6\)
- The gcd plays a big role in many number-theoretic arguments
we need for Shor's algorithm.
- Euclid's millenia-old algorithm is surprisingly efficient,
and can be written recursively.
- Just as importantly, Euclid's algorithm can be run in
"reverse" to solve for the coefficients in Bezout's Lemma.
- And a variation will be used in working with continued fractions.
- Bezout's Lemma:
- This basic result expresses the gcd as a linear combination:
there will always be integers \(r,s\) such that
$$
\gcd(a,b) \eql ra + sb
$$
- The result turns out to be quite useful as a building block
in many other results, especially in solving the single-variable
equation
$$
(ax \md M) \eql (b \md M )
$$
which we will also write as
$$
ax \; \equiv_M \; b
$$
- Being able to solve \(ax \equiv_M b\) is another useful
basic result:
- Solving \(ax \equiv_M 1\) gives us the modular inverse
of \(a\), analogous to \(zz^{-1} = 1\) for real or complex numbers.
- And the "reverse-Euclid" algorithm let's us calculate this
inverse directly.
- Finally, there's Fermat's Little Theorem:
If \(p\) is an odd prime then
$$
a^{p-1} \; \equiv_p \; 1
$$
for any positive integer \(a\) that is not a multiple of \(p\),
a result that is cleverly exploited in public-key cryptography (RSA).
- The "star" of this show is Euclid's algorithm, a 2000-year
old algorithm that appears in three different forms:
- As the original, in finding the gcd.
- As a Euclid-in-reverse variation, to solve
$$
\gcd(a,b) \eql ra + sb
$$
for integers \(r\) and \(s\).
- In constructing continued fractions and their so-called convergents.
Greatest common divisor (gcd) and Euclid's algorithm
Mod and div
- With integer division, as in \(\frac{14}{3}\), there is both
a quotient and remainder:
$$\eqb{
\frac{14}{3} & \eql & 4 & \;\;\;\; \mbox{ (quotient) } \\
14 \mbox{ mod } 3 & \eql & 2 & \;\;\;\; \mbox{ (remainder) } \\
}$$
- When dividing by \(3\), the only possible remainders are \(0, 1, 2\).
- When dividing by \(M\), the possible remainders are
$$
S_M \; \defn \; \setl{0,1,2,\ldots, M-1}
$$
- Consider \(14 \md 3\) and \(8 \md 3\):
$$\eqb{
14 \md 3 & \eql & 2 \\
8 \md 3 & \eql & 2
}$$
That is,
$$
14 \md 3 \eql 8 \md 3
$$
Both \(14\) and \(8\) have the same remainder when divided by 3.
- We can think of \(\md 3\) as a mapping:
$$
f_3(x) \eql x \md 3
$$
Then, we've seen that
$$
f_3(14) \eql f_3(8)
$$
That is, \(14\) and \(8\) are equivalent in this mapping
\(\rhd\)
They produce the same result
- This equivalence can be written in many ways:
$$\eqb{
14 \md 3 & \; = \; & 8 \md 3 \\
14 & \; =_3 \; & 8 \\
14 & \; \equiv \; & 8 \;\;\; (\md 3) \\
14 & \; \equiv_3 \; & 8 \;\;\; \\
}$$
- In general, if \(a, b, M \in \mathbb{Z}\) (the integers), then
we will write
$$
a \; \equiv_M \; b
$$
if \( (a \md M) = (b \md M)\).
Greatest common divisor (gcd):
- Consider numbers \(m=30, n=75\):
- \(5\) divides both \(30\) and \(75\).
- So does \(15\).
- In fact, \(15\) is the largest common divisor.
- Formally, for non-zero \(a,b\)
$$
\mbox{gcd}(a,b) \eql \mbox{ largest positive integer that
divides both \(a\) and \(b\)}
$$
- For our example, we could list the divisors of each:
$$\eqb{
\mbox{divisors of } 30 & \eql & \{1, 3, 5, 6, 10, {\bf 15}\} \\
\mbox{divisors of } 75 & \eql & \{1, 3, 5, {\bf 15}, 25\} \\
}$$
And then identify the common divisors:
$$
\mbox{common divisors of } 30, 75 \eql
\{1, 3, 5, {\bf 15}\}
$$
Then find the largest element in here.
- Alternatively, we could prime-factorize both,
identify the common primes, and multiply them:
$$\eqb{
30 & \eql & 2 \times {\bf 3} \times {\bf 5}\\
75 & \eql & {\bf 3} \times {\bf 5} \times 5\\
}$$
- There is a faster way: using Euclid's Algorithm.
Before getting to Euclid's algorithm, let's make a key observation:
- Suppose \(m \gt n\) and \(k\) divides both.
- Then, \(k\) divides any multiple of \(m\)
- And, \(k\) divides any multiple of \(n\)
- Thus, \(k\) divides any positive linear combination \((am + bn)\)
for integers \(a,b\).
- Example: \(5\) divides \(330\) and \(150\), so it divides,
\(2 \times 330 - 3 \times 150 = 210\).
- Thus,
\(k\) divides \((m - n), (m - 2n), (m - 3n) \ldots \)
(as long as they are positive)
- What is the smallest positive number in this list?
\(\rhd\)
\(m \md n\)
- So, \(k\) divides both \(n\) and \(m \md n\).
- Next, \(k\) also divides \(\gcd (n, m \md n)\)
- Consider this example: \(m=330, n=150\)
- Then \(m \md n = 330 \md 150 = 30\).
$$\eqb{
330 & \eql & {\bf 2} \times {\bf \underline{3}} \times {\bf \underline{5}} \times 11\\
30 & \eql & {\bf 2} \times {\bf \underline{3}} \times {\bf \underline{5}} \\
}$$
- Any number that divides both 330 and 30 (like \(3 \times 5\))
must divide \(\gcd (330,30)\)
- That's because it's in the product of common primes (the gcd):
$$
{\bf 2} \times {\bf \underline{3}} \times {\bf \underline{5}}
$$
- Now recall: \(k\) divides both \(m\) and \(n\)
- Amongst these \(k\) will be \(\gcd (m,n)\).
- Remember, \(k\) also divides \(\gcd (n, m \md n)\) (from above).
- So, \(\gcd (m,n)\) divides \(\gcd (n, m \md n)\).
- But \(\gcd (m,n)\) is the largest of such \(k\).
- Thus,
$$
\gcd(m, n) = \gcd (n, m \md n)
$$
- Example: \(m=330, n=150\)
$$\eqb{
330 & \eql & {\bf 2} \times {\bf \underline{3}} \times {\bf \underline{5}} \times 11\\
150 & \eql & {\bf 2} \times {\bf \underline{3}} \times {\bf
\underline{5}} \times 5\\
}$$
- The different \(k\) that divide both \(m=330, n=150\):
$$\eqb{
k_1 & \eql & 2 \times 3 \\
k_2 & \eql & 2 \times 5 \\
k_3 & \eql & 3 \times 5 \\
k_4 & \eql & 2 \times 3 \times 5 & \;\;\;\;\; \mbox{(the gcd)}\\
}$$
- We've shown that each of these \(k\)'s must divide
\(\gcd(150, 330\md 150) = \gcd(150,30)\).
- The largest such is \(2 \times 3 \times 5 = 30\).
- Which must be at least as large as \(\gcd(150, 30)\).
- Thus, \(\gcd(330,150) = \gcd(150, 30)\).
- Thus, we have the key insight:
$$
\gcd(m, n) = \gcd (n, m \md n)
$$
That is, to apply recursion.
Euclid's Algorithm:
- Example: \(m=75, n=30\):
- The gcd will divide these numbers:
$$\eqb{
& & 75\\
75-30 & \eql & 45\\
75-2(30) & \eql & 15
}$$
- The smallest number is \(75 \md 30 = 15\).
- The gcd of 75 and 30 must be the gcd of 30 and 15:
$$
\gcd(75, 30) \eql \gcd(30, 15)
$$
- We have reduced the problem to calculating \(\gcd(30, 15)\).
- Applying the same idea:
$$
\gcd(30, 15) \eql \gcd(15, 30 \md 15) \eql \gcd(15, 0) \eql 15
$$
- Example: \(m=102, n=30\):
- Here, in the first step, we observe:
$$
\gcd(102,30) \eql \gcd(30, 102\md 30) \eql \gcd(30, 12)
$$
- Now we are left with computing \(\gcd(30, 12)\):
$$
\gcd(30, 12) \eql \gcd(12, 30\md 12) \eql \gcd(12, 6)
$$
- Next,
$$
\gcd(12, 6) \eql \gcd(6, 12 \md 6) \eql \gcd(6, 0)
$$
- Then, when one of them is 0, the other is the gcd:
$$
\gcd(12, 6) \eql 6
$$
- Thus,
$$
\gcd(102, 30) \eql 6
$$
- Algorithm (Euclid):
Algorithm: gcd (m, n)
Input: integers m, n > 0
// See if parameters need to be swapped.
1. if n > m
2. return gcd (n,m)
3. endif
// The algorithm.
4. if n = 0
5. return m;
6. else
7. return gcd (n, m mod n)
8. endif
- Analysis:
- Note that \(m \md n \lt n\).
- If \(n \leq \frac{m}{2}\), then \(m \md n \;\;\lt \;\; n \;\;\leq \;\; \frac{m}{2}\).
- If \(n \gt \frac{m}{2}\), then \(m \md n \eql m - n \;\;\leq\;\;
\frac{m}{2}\).
- Thus, the larger number is reduced by at least
\(\frac{1}{2}\) each time.
\(\rhd\)
Thus, the running time is at most \(O(\log m)\).
In-Class Exercise 1:
Apply Euclid's algorithm to find \(\gcd(48,30)\).
Coprime:
- Two numbers \(a, b\) are coprime if \(\gcd(a,b) = 1\).
- That is, the largest positive common divisor is 1.
- Example: 8, 15
- Divisors of 8: \(\{1, 2, 4\}\)
- Divisors of 15: \(\{1, 3, 15\}\)
- \(\gcd(8,15) = 1\).
- Other equivalent terms: \(a,b\) are relatively prime,
or mutually prime.
Bezout's lemma and the extended Euclid algorithm
Proposition A.2.1: (Bezout's Lemma)
Let \(a, b\) be positive integers. Then there exist
integers \(r, s\) (possibly negative) such that
$$
\gcd(a,b) \eql ra + sb
$$
That is, the gcd can be expressed as a linear combination of
\(a\) and \(b\), allowing for negative integer coefficients.
Example:
- Suppose \(a=19, b=8\).
- Then, \(\gcd(19,8) = 1\).
- Can we find \(r, s\) such that
$$
1 \eql ra + sb \eql 19r + 8b?
$$
- Bezout's Lemma says, yes, there must be such integers:
$$
1 \eql 19 \times 3 \; + \; 8 \times (-7)
$$
That is, \(r=3, s=-7\).
Proof:
Let
$$
S \eql \{\mbox{all } ra+sb \mbox{ such that } ra+sb \gt 0 \}
$$
and let \(m\) be the smallest element in \(S\).
We'll show:
- \(\gcd(a,b) \leq m\)
- \(\gcd(a,b) \geq m\)
Which will mean \(m = \gcd(a,b)\) and the proof is complete.
- \(\gcd(a,b) \leq m\):
\(\gcd(a,b)\) divides both \(a\) and \(b\).
- Thus, it will divide multiples of each, and the sum of such multiples.
- Thus, it divides any element of \(S\), including \(m\).
- Because \(\gcd(a,b) \gt 0\), it must be that \(\gcd(a,b) \leq
m\).
- \(\gcd(a,b) \geq m\):
- We'll show that \(m\) divides \(a\). Assume to the contrary,
which means there will be a remainder.
- Recall: \(a, m\) are both positive.
- Let \(a = qm + p\), where \(p \lt m\) (the remainder), and
\(p \gt 0\).
- Substitute \(m = ra + sb\) (for some \(r, s\)):
$$
a \eql qm + p \eql qm + ra + sb
$$
or
$$
p \eql (1-qr) a + (-qs) b
$$
This is a linear combination of \(a,b\).
- By assumption \(p\lt m, p \gt 0\).
- This means we've found a smaller positive linear combination
in \(S\), a contradiction.
The exact same argument shows that \(m\) divides \(b\) and
therefore \(m \leq \gcd(a,b)\).
We now show how to compute the numbers \(r, s\) in
$$
\gcd(a,b) \eql ra + sb
$$
- First, recall the main idea in Euclid's algorithm:
- We're given \(m \gt n\) as input
- Then
$$
\gcd(m,n) \eql \gcd(n, m \md n)
$$
- Let's write the above a little differently:
- Let
$$
m \eql k n + r
$$
so that \(m \md n = r\)
- Then
$$
\gcd(m,n) \eql \gcd(n, r)
$$
- Example: \(m=19, n=8\)
$$\eqb{
\gcd(19,8) & \eql & \gcd(8, 19 \md 8) \\
& \eql & \gcd(8, 3)
}$$
- Next, let's explicitly write the \(m, n, k, r\) values at each step,
using subscript \(i\) for the i-th step:
$$\eqb{
19 & \eql & 2 (8) + 3 & \;\;\;\; &
\mbox{\(m_1=19, n_1=8, k_1=2, r_1=3\) } \\
8 & \eql & 2(3) + 2 & \;\;\;\; &
\mbox{\(m_2=n_1=8, n_2=r_1=3, k_2=2, r_2=2\) } \\
3 & \eql & 1(2) + 1 & \;\;\;\; &
\mbox{\(m_3=n_2=3, n_3=r_2=2, k_3=1, r_3=1\)} \\
2 & \eql & 2(1) + 0 & \;\;\;\; &
\mbox{\(m_4=n_3=2, n_4=r_3=1, k_4=1, r_4=0\), stop with \(\gcd
= g = n_4=r_3\)}
}$$
- Notice how \(r_i = n_{i+1} = m_{i+2}\)
- If we retain the numbers \(m_i,n_i,k_i, r_i\) at each
step, we can work backwards starting from the next-to-last step:
- Rewrite the next-to-last equation as
$$
g \eql 3 - 1(2) \eql m_3 - k_3(r_2)
$$
- Now substitute for \(r_2\) from the second equation
$$
g \eql 3 - 1( 8 - 2(3)) \eql m_3 - k_3(m_2 - k_2(r_1))
$$
and simplify (using \(m_3=r_1\)) to
$$
g \eql 3(3) - 8 \eql 3(r_1) - m_2
$$
- Finally, substitute for \(r_1\):
$$
g \eql 3(m-2n) - n \eql 3m - 7n
$$
- Thus, we've expressed the \(\gcd\) in terms of the original \(m,n\)
as in Bezout's lemma.
In-Class Exercise 2:
Apply Euclid's algorithm in reverse to find the
numbers \(r,s\) such that \(\gcd(48,30) = 48r + 30s\).
Solving \(ax \; \equiv_M \; b\)
Proposition A.2.2:
If \(\gcd(a, M)=1\) then the equation in \(x\)
$$
ax \; \equiv_M \; b
$$
has a finite solution.
Proof:
From Bezout's Lemma above, we can express \(\gcd(a,M)=1\) as
a linear combination
$$
1 \eql ra + sM
$$
Multiple both sides by \(b\):
$$
a(br) + M (bs) \eql b
$$
Dividing by \(M\) on the left side results in the
remainder \(a(br)\). On the right side, we have \(b \md M\).
Thus,
$$
a(br) \md M \eql b \md M
$$
And so, \(x=br\) is a solution to
$$
ax \; \equiv_M \; b
$$
Proposition A.2.3:
If \(x=c\) is a solution to the equation
$$
ax \; \equiv_M \; b
$$
then so is \(y = c \md M\).
Proof:
Since
$$
y \eql c \md M
$$
multiply both sides by \(a\) to get
$$
ay \eql ac \md M
$$
But the right side is \(b \md M\) since \(c\) is a solution. Thus,
$$
ay \eql b \md M
$$
which we can write as
$$
ay \; \equiv_M \; b
$$
Thus, \(y\) is a solution.
An example:
- Suppose we're given \(a=3, M=7\) and wish to solve
$$
3x \; \equiv_7 \; 5
$$
- Apply reverse-Euclid in Bezout's Lemma, we get
$$
1 \eql 1(7) - 2(3)
$$
and so \(r=-2\).
- This means \(x = br = -10\) is a solution.
- For the smallest positive solution, we add enough multiples
of \(M=7\) to get \(-10 + 2(7) = 4\):
$$
3 \times 4 \; \equiv_7 \; 5
$$
- Another solution, for example is
$$
3 \times 18 \; \equiv_7 \; 5
$$
- From A.2.3, \(18 \md 7 = 4\) is also a solution, which
we saw earlier.
Proposition A.2.4:
If \(\gcd(a,M) = 1\) and
$$
ab \; \equiv_M \; a
$$
then
$$
b \; \equiv_M \; 1
$$
The converse also holds: if \(b \equiv_M 1\), then \(ab \equiv_M a\).
Proof:
The forward direction follows from the previous result.
For the reverse direction, because \(b \equiv_M 1\), there
is some \(k\) such that \(b = kM + 1\). Then,
\(ab = akM + a\) from which \(ab \md M = a \md M\).
Modular inverse
Proposition A.2.5:
If \(\gcd(a, M)=1\), \(M\gt 1\), and \(a \lt M\) then there
is a unique element \(a^\ast\) in \(S_M=\{1,2,\ldots, M-1\}\) such that
$$
a a^\ast \; \equiv_M \; 1
$$
The number \(a^\ast\) is the inverse of \(a\) with respect to
multiplication modulo-\(M\).
Proof:
Since \(\gcd(a,M)=1\) then, by Bezout's Lemma above, we can write
$$
a \eql ra + sM
$$
Rearranging,
$$
ra - 1 \eql M(-s)
$$
Which means \(M\) divides \(ra-1\) or
$$
ra \md M \eql 1
$$
Now define
$$
a^\ast \eql r \md M
$$
Then all we need to do is show that it is unique.
Suppose there exists \(c\) such that
$$
a c \; \equiv_M \; 1
$$
Then, because \(a a^\ast \equiv_M 1\),
$$
a c \; \equiv_M \; a a^\ast
$$
Or
$$
c \eql a^\ast \md M
$$
Computing the modular inverse:
- Given \(a, M\) such that \(\gcd(a,M)=1\), we would like to
compute the inverse \(a^\ast\) such that
$$
a a^\ast \; \equiv_M \; 1
$$
- From Bezout's algorithm, we can compute \(r, s\) such that
$$
ra + sM \eql 1
$$
- Then,
$$
ra - 1 \eql (-s) M
$$
and thus
$$
ra - 1 \; \equiv_M \; 0
$$
- From which
$$
ra \; \equiv_M \; 1
$$
- And so, \(a^\ast = r\).
Example:
- Suppose we want the modular inverse of \(a=3\) with \(M=7\).
- We saw earlier that in solving \(\gcd(3,7)=1\)
$$
-2(3) + 1(7) \eql 1
$$
- And so, \(r=-2\) is an inverse.
- The smallest positive inverse adds a multiple of \(7\) so
that the result lies in \(\{0,\ldots,6\}\):
$$
-2 + 7 \eql 5
$$
and hence \(5\) is the modular inverse:
$$
3 \times 5 \; \equiv_7 \; 1
$$
A special case of the Chinese Remainder Theorem
We will only consider this special case:
-
Proposition A.2.6:
Suppose \(x, p, q\) and \(m\) are integers with \(p,q\) coprime,
and that
$$\eqb{
x \md p & \eql & m \\
x \md q & \eql & m \\
}$$
Then
$$
x \md pq \eql m \\
$$
Proof:
- Write
$$\eqb{
x & \eql & k_1 p + m \\
x & \eql & k_2 p + m \\
}$$
with the quotients \(k_1, k_2\).
- Then, equating the two, we
see that
$$
k_1 p \eql k_2 q
$$
We'll call this number \(y = k_1p = k_2 q\).
- Then, \(y\) is a multiple of both \(p\) and \(q\)
and thus a multiple of \(\mbox{LCM}(p,q)\).
- But because \(p,q\) are coprime by assumption, the LCM is \(pq\).
- Which means \(k_1p\) (and \(k_2q\)) is a multiple of \(pq\),
say \(kpq\).
- Thus, we can write \(x = k_1p + m\) as
$$
x \eql kpq + m
$$
Which makes \(x \md pq = m\).
Note: the result holds even when the remainder \(m = 0\). We will need
to remember this when proving the correctness of RSA.
Fermat's little theorem
Proposition A.2.7: (Fermat's Little Theorem)
If \(p\) is a prime then
$$
a^{p-1} \; \equiv_p \; 1
$$
for any positive integer \(a\) that is not a multiple of \(p\).
Proof:
Let \(m\) be any positive integer. We'll show that
$$
m^p - m \; \equiv_p \; 0
$$
Then, if this is true, it's true for \(a\):
$$
a^p - a \; \equiv_p \; 0
$$
or
$$
a(a^{p-1} - 1) \; \equiv_p \; 0
$$
By assumption, \(a\) is not divisible by \(p\) and so
$$
a^{p-1} - 1 \; \equiv_p \; 0
$$
Or
$$
a^{p-1} \; \equiv_p \; 1
$$
Let's now prove
$$
m^p - m \; \equiv_p \; 0
$$
by induction for any positive \(m\):
- It's certainly true for \(m=1\).
- Assume it's true for \(m=k\).
- Now
$$
(k+1)^p - (k+1)
\eql
k^p + \nchoose{p}{1} k^{p-1} + \nchoose{p}{2} k^{p-2} + \ldots
+ + \nchoose{p}{p-1} k^{1} + 1^p - (k+1)
$$
- Every \(\nchoose{p}{i}\) is a multiple of \(p\), and so all the
terms involving \(\nchoose{p}{i}\) are multiples of \(p\).
(They are multiplied by an integer).
- Then
$$
(k+1)^p - (k+1)
\; \equiv_p \;
k^p + 1 - (k+1) \; = \; k^p - k
$$
But the latter is true because of the induction hypothesis.
Example:
- With \(a=10, p=7\), clearly the conditions are satisfied:
- 7 is an odd prime
- 10 is not a multiple of 7
- Then \(10^(7-1) \md 7 = 10^6 \md 7 = 1\).
Continued fractions and convergents
Let's start with an example and work through a few
calculations, introducing the ideas as we proceed:
- Consider the number defined by the following
operations:
$$
0 + \cfrac1{ 1 + \cfrac1{ 1 + \cfrac1{ 7 + \frac{1}{2}} } }
$$
- We will evaluate this expression by starting at the bottom,
working "upwards", and keeping the rational form:
$$\eqb{
0 + \cfrac1{ 1 + \cfrac1{ 1 + \cfrac1{ 7 + \frac{1}{2}} } }
& \eql &
0 + \cfrac1{ 1 + \cfrac1{ 1 + \frac{1}{15/2}} } \\
& \eql &
0 + \cfrac1{ 1 + \cfrac1{ 1 + \frac{2}{15}} } \\
& \eql &
0 + \cfrac1{ 1 + \frac{1}{17/15} } \\
& \eql &
0 + \cfrac1{ 1 + \frac{15}{17} } \\
& \eql &
0 + \frac{1}{32/17} \\
& \eql &
\frac{17}{32}\\
}$$
Note:
- Going backwards in the steps above
is a way to start with a rational and produce its continued fraction.
- There is a simpler algorithm for this, described below.
produce
In-Class Exercise 3:
Evaluate the expression
$$
0 + \cfrac1{ 2 + \cfrac1{ 2 + \frac{1}{6}} }
$$
- In general, a continued fraction can be finite or
infinite:
$$
n_1 +
\cfrac{m_2}{n_2 + \cfrac{m_3}{n_3 + \ddots}}
$$
- We will focus on finite continued fractions where the
numerators are all 1, such as:
$$
n_1 +
\cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4 + \frac{1}{n_5}}}}
$$
- In our example
\(n_1=0, n_2=1, n_3=1, n_4=7, n_5=2\):
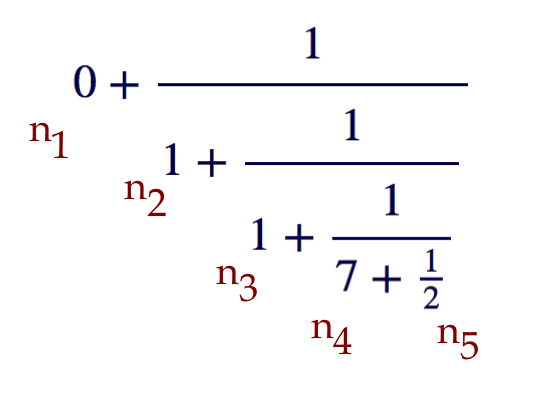
- Next, define a series of approximating convergents
(using our example):
$$\eqb{
g_1 & \eql & n_1 + \cfrac1{n_2}
& \eql & 0 + \cfrac1{1}
& \eql & 1 \\
g_2 & \eql & n_1 + \cfrac1{n_2 + \cfrac1{n_3}}
& \eql & 0 + \cfrac1{1 + \cfrac1{1}}
& \eql & \frac{1}{2} \\
g_3 & \eql & n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4}}}
& \eql & 0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7}}}
& \eql & \frac{8}{15} \\
g_4 & \eql & n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4 + \cfrac1{2}}}}
& \eql & 0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7 + \cfrac1{2}}}}
& \eql & \frac{17}{32} \\
}$$
- Think of the convergents as successively better
approximations to the original rational number \(\frac{17}{32}\).
In-Class Exercise 4:
What are the convergents for
$$
0 + \cfrac1{ 2 + \cfrac1{ 2 + \frac{1}{6}} }?
$$
Next, let's set about calculating a continued fraction
for a given rational:
- What we'll see is something very similar to Euclid's algorithm,
successively using remainders.
- Let's work through an example: \(\frac{17}{32}\).
- We're given \(\frac{a}{b} = \frac{17}{32}\).
- Then, let
$$\eqb{
n_1 & \eql & a \mbox{ div } b & \eql & 17 \mbox{ div } 32 & \eql & 0\\
r_1 & \eql & a \mbox{ mod } b & \eql & 17 \mbox{ mod } 32 & \eql & 17\\
}$$
Thus,
$$
n_1 + \frac{r_1}{b} \eql 0 + \frac{17}{32}
$$
We will set \(r_0 = b\) and write this as:
$$
\frac{17}{32} \eql n_1 + \frac{r_1}{r_0} \eql 0 + \frac{17}{32}
$$
- Next, calculate
$$\eqb{
n_2 & \eql & r_0 \mbox{ div } r_1 & \eql & 32 \mbox{ div } 17 & \eql & 1\\
r_2 & \eql & r_0 \mbox{ mod } r_1 & \eql & 32 \mbox{ mod } 17 & \eql & 15\\
}$$
Thus,
$$
\frac{17}{32} \eql n_1 + \cfrac1{n_2 + \frac{r_2}{r_1}}
\eql
0 + \cfrac1{1 + \frac{15}{17}}
$$
- We can now see the logic:
- The next step is to invert \(\frac{15}{17}\)
$$
0 + \cfrac1{1 + \frac{1}{17/15}}
$$
- And then break out \(\frac{17}{15}\) into a quotient and remainder:
\(\frac{17}{15} = 1 + \frac{2}{15}\)
$$
0 + \cfrac1{1 + \cfrac1{1 + \frac{2}{15}}}
$$
- Using our notation, we have calculated
$$\eqb{
n_3 & \eql & r_1 \mbox{ div } r_2 & \eql & 17 \mbox{ div } 15 & \eql & 1\\
r_3 & \eql & r_1 \mbox{ mod } r_2 & \eql & 17 \mbox{ mod } 15 & \eql & 2\\
}$$
and thus our expression is
$$
\frac{17}{32}
\eql
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \frac{r_3}{r_2}}}
\eql
0 + \cfrac1{1 + \cfrac1{1 + \frac{2}{15}}}
$$
- The next step is
$$\eqb{
n_4 & \eql & r_2 \mbox{ div } r_3 & \eql & 15 \mbox{ div } 2 & \eql & 7\\
r_4 & \eql & r_2 \mbox{ mod } r_3 & \eql & 15 \mbox{ mod } 2 & \eql & 1\\
}$$
to give
$$
\frac{17}{32}
\eql
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4 + \frac{r_4}{r_3}}}}
\eql
0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7 + \frac{1}{2}}}}
$$
- Finally, because the next step results in a remainder of 0,
we stop:
$$\eqb{
n_5 & \eql & r_3 \mbox{ div } r_4 & \eql & 2 \mbox{ div } 1 & \eql & 2\\
r_5 & \eql & r_3 \mbox{ mod } r_4 & \eql & 2 \mbox{ mod } 1 & \eql & 0\\
}$$
This leaves the final expression
$$
\frac{17}{32}
\eql
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4 + \cfrac1{n_5}}}}
\eql
0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7 + \frac{1}{2}}}}
$$
with \(n_1=0, n_2=1, n_3=1, n_4=7, n_5=2\).
- Thus, given a rational \(\frac{a}{b}\), with \(r_0=b\),
we compute
$$\eqb{
n_1 & \eql & a \mbox{ div } b \\
r_1 & \eql & a \mbox{ mod } b \\
}$$
and then, for \(k\gt 1\)
$$\eqb{
n_k & \eql & r_{k-2} \mbox{ div } r_{k-1} \\
r_k & \eql & r_{k-2} \mbox{ mod } r_{k-1} \\
}$$
until such \(k\) where \(r_k=0\).
- Then, the sequence of integers
\(n_1, n_2,\ldots, n_k\)
in continued fraction form is equal to the rational \(\frac{a}{b}\).
- The process ends because, if we examine only the
recurrence for the remainder
$$
r_k \eql r_{k-2} \mbox{ mod } r_{k-1} \\
$$
the remainders are a strictly decreasing positive sequence
just like the one in Euclid's algorithm.
In-Class Exercise 5:
Work through the recurrence above for the rational \(\frac{13}{32}\).
To find the convergents, one can work backwards as in the
reverse-Euclid approach:
- Suppose we have
$$
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4 + \cfrac1{n_5}}}}
$$
- The next approximating convergent comes from removing
\(n_5\):
$$
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4}}}
$$
- We want to calculate the integers in this rational number.
- Define integers \(p_i, q_i\) where the denominator
at the level that contains \(n_i\) is
$$
n_i + \frac{1}{p_{i+1}/q_{i+1}} \eql n_i + \frac{q_{i+1}}{p_{i+1}}
$$
Then, simplifying, we get
$$
\frac{ n_i p_{i+1} + q_{i+1} }{ p_{i+1} }
$$
But this is \(\frac{p_i}{q_i}\), that is,
$$
\frac{p_i}{q_i} \eql \frac{ n_i p_{i+1} + q_{i+1} }{ p_{i+1} }
$$
- Now we can write our backwards recurrence as:
$$\eqb{
p_i & \eql & n_i p_{i+1} + q_{i+1} \\
q_i & \eql & p_{i+1}
}$$
- For example, suppose we want to simplify the
convergent
$$
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \cfrac1{n_4}}}
\eql
0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7}}}
$$
- First start with
$$
n_1 + \cfrac1{n_2 + \cfrac1{n_3 + \frac{q_4}{p_4}}}
\eql
0 + \cfrac1{1 + \cfrac1{1 + \cfrac1{7}}}
$$
and simplify
$$
n_3 + \frac{q_4}{p_4}
\eql
\frac{p_4 n_3 + q_4}{p_4}
\eql
\frac{1 \times 7 + 1}{7}
\eql
\frac{8}{7}
\eql
\frac{p_3}{q_3}
$$
- After which
$$
n_2 + \frac{q_3}{p_3}
\eql
1 + \frac{7}{8}
\eql
\frac{15}{8}
\eql
\frac{p_2}{q_2}
$$
- And finally
$$
n_1 + \frac{q_2}{p_2}
\eql
0 + \frac{8}{15}
\eql \frac{8}{15}
$$
- We have thus calculated the convergent \(g_3=\frac{8}{15}\).
Finally, a powerful result about rationals and
continued-fraction convergents: