Goals
The DFT is a linear transformation
takes as input a vector of complex numbers, and
produces a same-size vector of complex numbers.
Thus, the DFT is a square matrix.
(And so is its inverse.)
The action of applying the DFT or its inverse could
be considered an algorithm.
As an algorithm, it is one of the most important and useful
algorithms of all time with direct applications in:
- Signal and image processing.
- Data compression (JPG, MPEG)
As a mathematical technique, it is equally useful in:
- Analyzing approaches to signals, images, data compression.
- As an approximation to Fourier series applied to solving
differential equations.
We want to introduce the DFT, with just enough detail to
apply to quantum computing:
- What exactly is this square matrix?
- Why is it useful?
- The version that's unitary.
- Conventions in sign.
D.1
N-th roots of 1
Define the complex numbers
$$\eqb{
\wn & \eql & e^{ \frac{2\pi i}{N} } \\
\wn^\ast & \eql & e^{ -\frac{2\pi i}{N} } \\
}$$
- Recall:
$$\eqb{
e^{2\pi i} & \eql & \cos(2\pi) + i \sin(2\pi) \eql 1 \\
e^{-2\pi i} & \eql & \cos(-2\pi) + i \sin(-2\pi) \eql 1 \\
}$$
- Each is an N-th root of \(1\) because
$$\eqb{
(\wn)^N & \eql & \parenl{ e^{ \frac{2\pi i}{N} } }^N
& \eql & e^{2\pi i} & \eql & 1\\
(\wn^\ast)^N & \eql & \parenl{ e^{ -\frac{2\pi i}{N} } }^N
& \eql & e^{-2\pi i} & \eql & 1\\
}$$
- Consider \(N=8\) as an example:
$$\eqb{
\wn & \eql & w_{8} \\
& \eql & e^{\frac{2\pi i}{8}} \\
& \eql & e^{ \frac{\pi}{4} } \\
& \eql & \cos \sml{\frac{\pi}{4}} + i \sin \sml{\frac{\pi}{4}} \\
& \eql & \sml{\isqt{1}} + i \sml{\isqt{1}}
}$$
Let's draw an arrow on the complex plane where the tip is
\(w_{8}\):
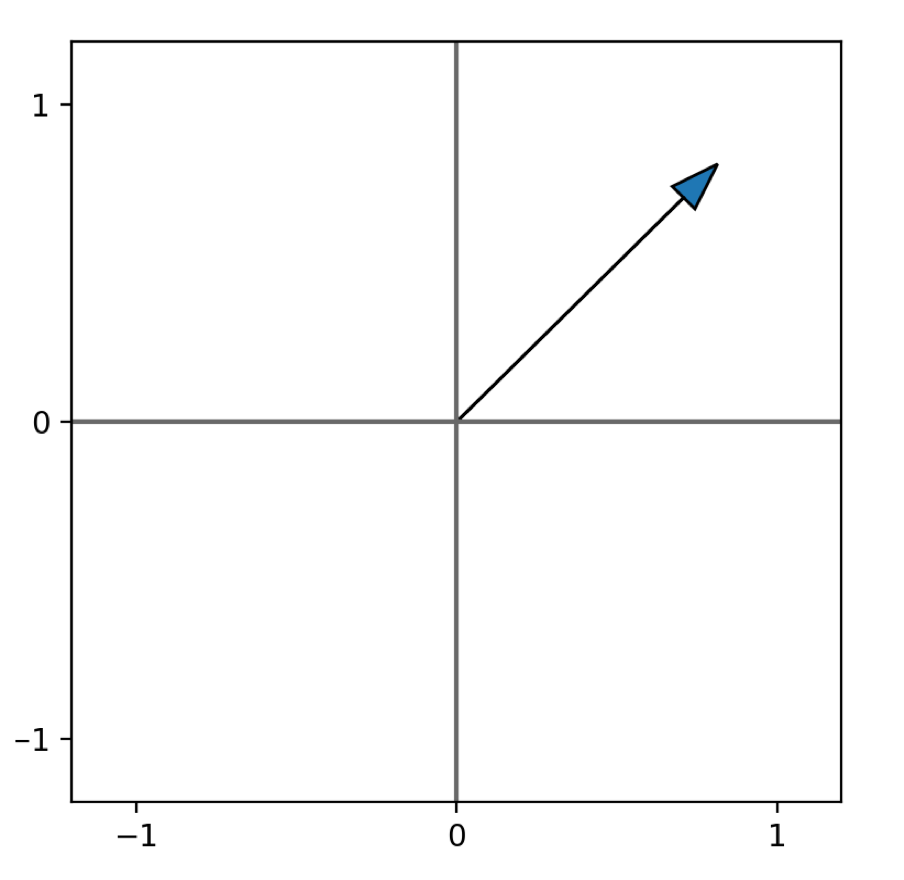
- Note:
- The arrow above is NOT a vector.
- It merely represents a number on the complex plane.
- We've drawn an arrow because it will be conceptually useful below.
What are the other N-th roots of 1?
- Consider \(k \in \{0,1,\ldots, N-1\}\). Then
$$\eqb{
\wn^k & \eql & \parenl{ e^{\frac{2\pi i}{N}} }^k \\
& \eql & e^{\frac{2\pi k i}{N}} \\
}$$
- When \(N\) is clear, from the context, we'll simplify
by leaving it out of the subscript:
$$
w^k \eql e^{\frac{2\pi k i}{N}}
$$
- Next, consider the N-th power:
$$\eqb{
(w^k)^N & \eql & \parenl{ e^{\frac{2\pi k i}{N}} }^N \\
& \eql & e^{2\pi k i} \\
& \eql & \left( e^{2\pi i} \right)^k \\
& \eql & (1)^k \\
& \eql & 1
}$$
- Thus, each of \(w^k\) for any integer \(k\) is an N-th
root of \(1\).
- Since there are \(N\) \(N\)-th roots of \(1\), we'll use the
term principal \(N\)-th root for \(w=e^{ \frac{2\pi i}{N}}\).
- But \(w^{k} = w^{k+pN}\), for any integer \(p\),
and so there are only \(N\) unique such roots.
- To clarify, let's write and then draw all 8 for the \(N=8\)
case, using \((a,b)\) as coordinates for the complex number \(a+ib\):
$$\eqb{
w^0 & \eql & e^{ \frac{2\pi 0 i}{8} } & \eql & 1 & \eql & (1,0) \\
w & \eql & e^{ \frac{2\pi i}{8} } & \eql & \smm{\isqt{1}} + i \smm{\isqt{1}}
& \eql & (\smm{\isqt{1}, \isqt{1}}) \\
w^2 & \eql & e^{ \frac{2\pi 2 i}{8} } & \eql & i
& \eql & (0, 1) \\
w^3 & \eql & e^{ \frac{2\pi 3 i}{8} } & \eql & \smm{-\isqt{1}} + i \smm{\isqt{1}}
& \eql & (-\smm{\isqt{1}, \isqt{1}}) \\
w^4 & \eql & e^{ \frac{2\pi 4 i}{8} } & \eql & -1
& \eql & (-1, 0) \\
w^5 & \eql & e^{ \frac{2\pi 5 i}{8} } & \eql & \smm{-\isqt{1}} - i \smm{\isqt{1}}
& \eql & (\smm{-\isqt{1}, -\isqt{1}}) \\
w^6 & \eql & e^{ \frac{2\pi 6 i}{8} } & \eql & - i
& \eql & (0, -1) \\
w^7 & \eql & e^{ \frac{2\pi 7 i}{8} } & \eql & \smm{\isqt{1}} - i \smm{\isqt{1}}
& \eql & (\smm{\isqt{1}, -\isqt{1}}) \\
}$$
- Next, drawing them with our arrows, we get:
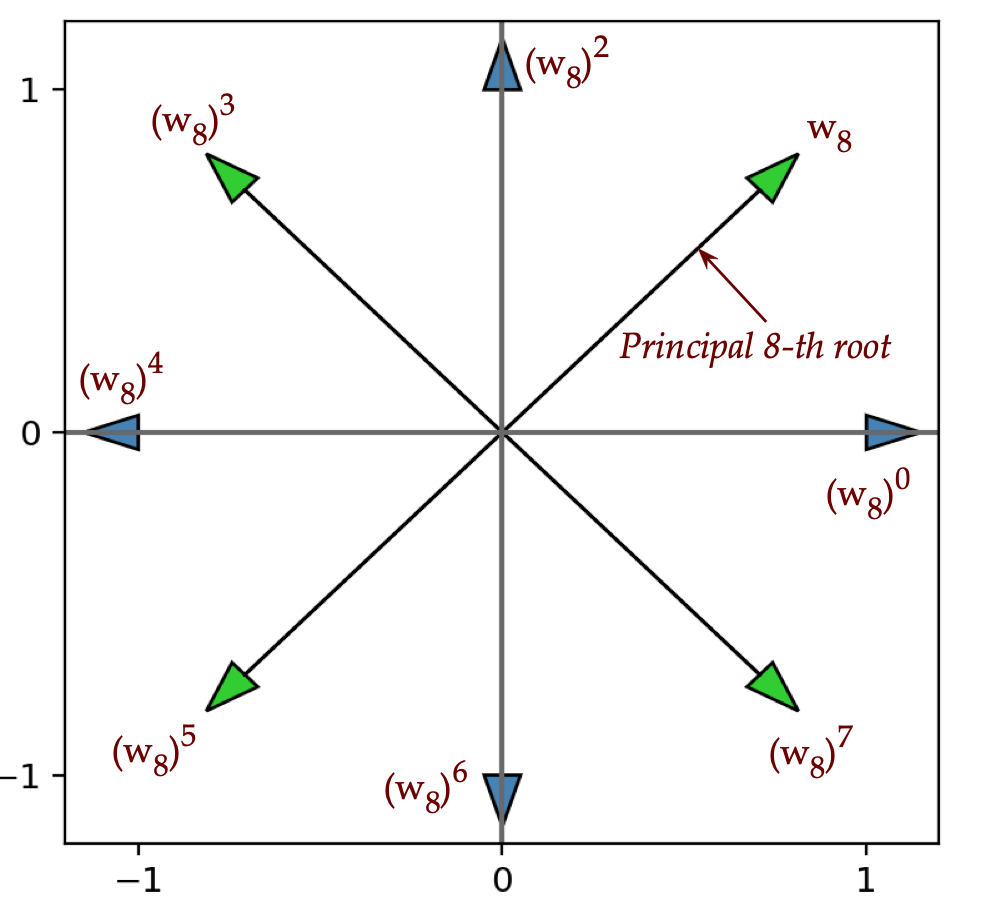
Observe:
- The arrows are of unit length since each \(w^k\) has unit-length.
- They are equally spaced since
$$
e^{ \frac{2\pi k i}{N} } \eql e^{ \frac{2\pi (k-1) i}{N} + \frac{2\pi i}{N} }
$$
That is, the angle increment is \(\frac{2\pi}{N}\).
- Next, a useful property:
$$\eqb{
w^0 + w^1 + \ldots + w^{N-1}
& \eql & \frac{1 - w^N}{1 - w} \\
& \eql & \frac{1 - 1}{1 - w} \\
& \eql & 0
}$$
since \(w^N = 1\) (by virtue of being an N-th root of \(1\)).
- Notice how the figure above confirms this:
- Think of the arrows as real vectors, as perhaps forces pulling.
- The sum is a net (force) of \(0\).
- This summation-to-zero
also applies to any equally spaced subset of these that go around:
- For example, consider \(N=12\).
- Suppose we start at \(w_{12}^2\) and skip two arrows each
time:
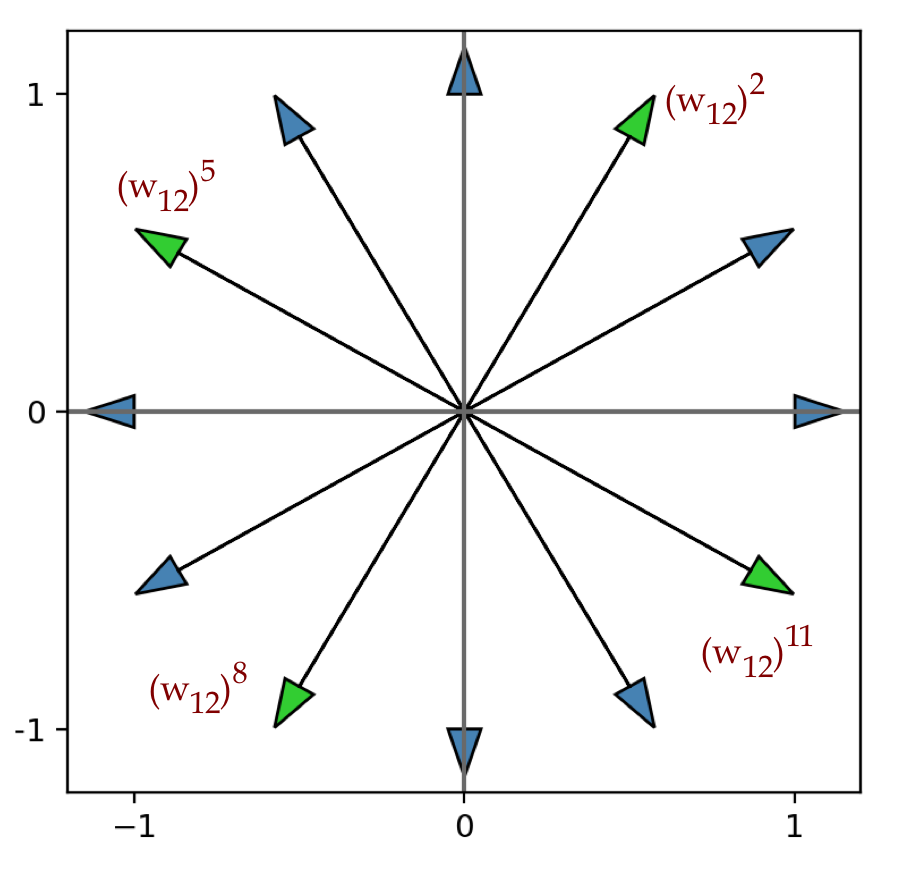
- These sum to \(0\) as well (by the vector argument).
- We can see this algebraically (leaving the subscript out):
$$\eqb{
w^2 + w^5 + w^8 + w^{11}
& \eql & w^2(1 + w^3 + w^6 + w^9) \\
& \eql & w^2(1 + w^3 + (w^3)^2 + (w^3)^3) \\
& \eql & w^2 \frac{1 - (w^3)^4}{1 - w^3} \\
& \eql & w^2 \frac{1 - w^{12}}{1 - w^3} \\
& \eql & w^2 \frac{1 - 1}{1 - w^3} \\
& \eql & 0
}$$
because \(w^{12}=1\).
- Notice the difference between the sum and the sum of squared magnitudes:
$$
\magsq{w^0} + \magsq{w^1} + \ldots + \magsq{w^{N-1}}
\eql 1 + 1 + \ldots + 1 \eql N
$$
Why is this true?
- Each \(w^k = e^{\frac{2\pi k i}{N}} = e^{i\theta}\) for
\(\theta = \frac{2\pi k}{N}\).
- Any complex number of the form \(re^{i\theta}\) has magnitude
\(1\) when \(r=1\).
Consider this picture:
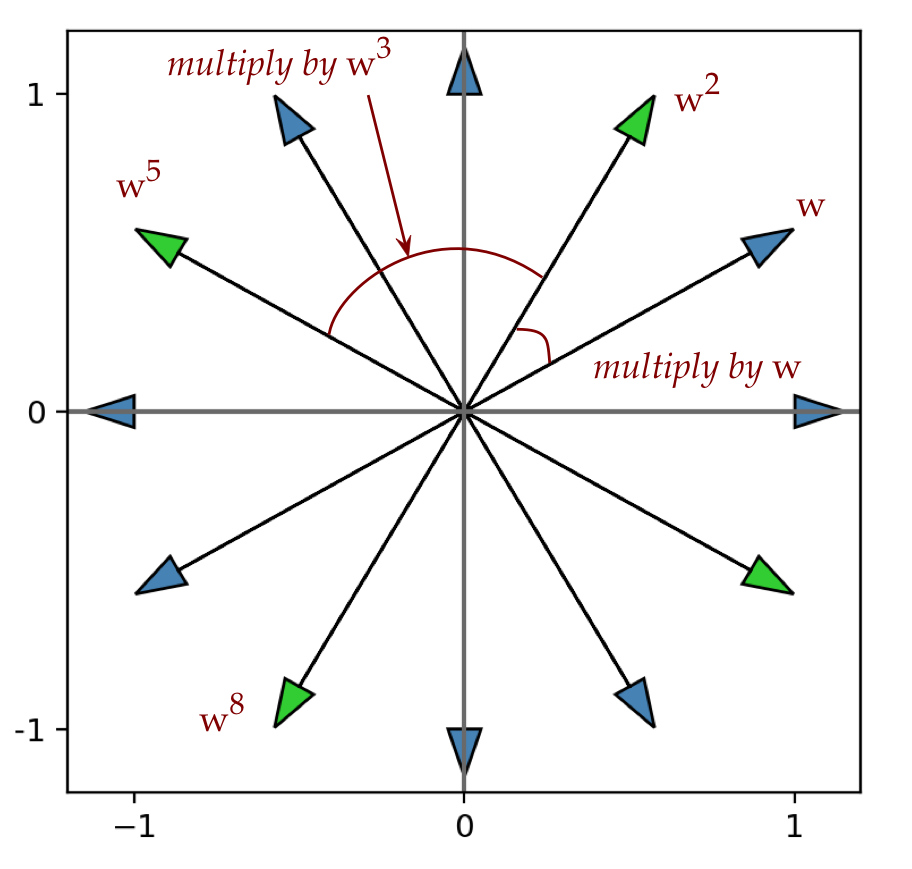
- This shows that to get from \(w\) to \(w^2\), we just
multiply by \(w\).
- Similarly, to get from \(w^2\) to \(w^5\) we multiply
\(w^2\) by \(w^3 = w^{5-2}\).
- Thus, if one starts with \(w^0\) and we skip every other
smallest-angle, we will get:
\((w^0, w^2, w^4, w^6, \ldots)\).
- When skipping thrice the smallest angle:
\((w^0, w^3, w^6, w^9, \ldots)\).
- We could also skip zero times the angle:
\((w^0, w^0, w^0, w^0, \ldots) = (1,1,1,\ldots)\).
- These vectors (like \((w^0, w^3, w^6, w^9, \ldots)\))
will become the columns of the DFT matrix.
D.2
Towards the DFT matrix
We're now going to place powers of \(w\) in an \(N \times N\) matrix:
- Let's look at \(N=4\) first:
$$
D \eql
\mat{
1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 \\
1 & w^2 & w^4 & w^6 \\
1 & w^3 & w^6 & w^9 \\
}
$$
Note:
- Here, \(w = w_4\), the primary 4-th root \(w_4 = e^{ \frac{2\pi i}{4}}\).
- The matrix is symmetric.
- It is not unitary because, at the very least, the first row
and column aren't unit-length.
- The first column is the zero-angle skip.
- The second skips by \(w\), the third by \(w^2\),
the fourth by \(w^3\).
- Next, consider \(N=8\):
$$
D \eql
\mat{
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 & w^4 & w^5 & w^6 & w^7\\
1 & w^2 & w^4 & w^6 & w^8 & w^{10} & w^{12} & w^{14}\\
1 & w^3 & w^6 & w^9 & w^{12} & w^{15} & w^{18} & w^{21}\\
1 & w^4 & w^8 & w^{12} & w^{16} & w^{20} & w^{24} & w^{28}\\
1 & w^5 & w^{10} & w^{15} & w^{20} & w^{25} & w^{30} & w^{35}\\
1 & w^6 & w^{12} & w^{18} & w^{24} & w^{30} & w^{36} & w^{42}\\
1 & w^7 & w^{14} & w^{21} & w^{28} & w^{35} & w^{42} & w^{49}\\
}
$$
- From this, we see the pattern:
$$
D \eql
\mat{
1 & 1 & 1 & \ldots & 1 \\
1 & w & w^2 & \ldots & w^{N-1} \\
1 & w^2 & w^4 & \ldots & w^{2(N-1)} \\
1 & w^3 & w^6 & \ldots & w^{3(N-1)} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
1 & w^k & (w^k)^2 & \ldots & w^{k(N-1)} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
1 & w^{N-1} & w^{2(N-1)} & \ldots & w^{(N-1)(N-1)}
}
$$
- Think of each column as representing a different
skip-angle.
- Because it's symmetric, the successive rows also represent
the same.
In-Class Exercise 1:
Write down the matrix for \(N=6\).
What does this matrix do when applied to vectors?
- Consider the vector of all \(1\)'s:
\(v=(1,1,\ldots, 1)\), for example with \(N=8\):
$$
Dv
\eql
\mat{
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 & w^4 & w^5 & w^6 & w^7\\
1 & w^2 & w^4 & w^6 & w^8 & w^{10} & w^{12} & w^{14}\\
1 & w^3 & w^6 & w^9 & w^{12} & w^{15} & w^{18} & w^{21}\\
1 & w^4 & w^8 & w^{12} & w^{16} & w^{20} & w^{24} & w^{28}\\
1 & w^5 & w^{10} & w^{15} & w^{20} & w^{25} & w^{30} & w^{35}\\
1 & w^6 & w^{12} & w^{18} & w^{24} & w^{30} & w^{36} & w^{42}\\
1 & w^7 & w^{14} & w^{21} & w^{28} & w^{35} & w^{42} & w^{49}\\
}
\mat{1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\ 1\\}
$$
- This results in computing row sums.
- For example, the 4th row multiplying into \(v\) produces
$$\eqb{
1 + w^3 + w^6 + w^9 + w^{12} + w^{15} + w^{18} + w^{21}
& \eql &
1 + w^3 + (w^3)^2 + (w^3)^3 + (w^3)^4 + (w^3)^5 + (w^3)^6 + (w^3)^7 \\
& \eql &
\frac{1 - (w^3)^8}{1 - w^3} \\
& \eql &
\frac{1 - w^{24}}{1 - w^3} \\
& \eql &
\frac{1 - (w^{8})^3}{1 - w^3} \\
& \eql &
\frac{1 - (1)^3}{1 - w^3} \\
& \eql & 0
}$$
- This shouldn't be surprising because it corresponds to adding
equally spaced arrows around the circle of arrows.
- The only exception is the first row (which represents only
one arrow, the arrow \((1,0)\)).
- Thus, because the matrix is symmetric, we've shown:
row and column sums are \(0\), except for the first row and first column.
- We've also shown:
the inner product of the first row with any other row is \(0\):
$$
\inrh{\mbox{first-row}}{\mbox{row-3}}
\eql
1 + w^3 + w^6 + w^9 + w^{12} + w^{15} + w^{18} + w^{21}
\eql 0
$$
(from above).
- Now consider the inner product between any two rows other
than the first, say row \(p\) and row \(q\):
$$\eqb{
\inrh{\mbox{row-p}}{\mbox{row-q}}
& \eql &
1 + (w^p)^* (w^q) + (w^{2p})^* (w^{2q}) + \ldots +
(w^{p(N-1)})^* (w^{q(N-1)})
& \mbx{Remember: left-side conjugation} \\
& \eql &
1 + w^{-p} w^q + w^{-2p} w^{2q} + \ldots +
w^{-p(N-1)} w^{q(N-1)}
& \mbx{\((w^k)^* = w^{-k}\)} \\
& \eql &
1 + w^{q-p} + (w^{q-p})^2 + \ldots +
(w^{q-p})^{(N-1)}
& \mbx{Exponent algebra} \\
& \eql &
\frac{1 - (w^{q-p})^{N}}{1 - w^{q-p}}
& \mbx{Geometric series} \\
& \eql &
\frac{1 - (w^{N})^{q-p}}{1 - w^{q-p}}
& \mbx{Exponent algebra} \\
& \eql &
\frac{1 - (1)^{q-p}}{1 - w^{q-p}}
& \mbx{\(w\) is an N-th root} \\
& \eql &
0
}$$
- Thus, we've shown:
- Sum of squared magnitudes across rows (columns) is: \(N\).
- Row (column) inner products are zero for different rows (columns).
Thus, \(D\) is orthogonal but not orthonormal.
- Now consider the adjoint \(D^\dagger\) with \(N=4\)
as an example:
Here,
$$
D \eql \mat{
1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 \\
1 & w^2 & w^4 & w^6 \\
1 & w^3 & w^6 & w^9 \\
}
$$
And so
$$\eqb{
D^\dagger
& \eql &
(D^*)^T \\
& \eql &
\left(
\mat{
1 & 1 & 1 & 1 \\
1 & w^* & (w^2)^* & (w^3)^* \\
1 & (w^2)^* & (w^4)^* & (w^6)^* \\
1 & (w^3)^* & (w^6)^* & (w^9)^* \\
}
\right)^T \\
& \eql &
\left(
\mat{
1 & 1 & 1 & 1 \\
1 & w^* & (w^*)^2 & (w^*)^3 \\
1 & (w^*)^2 & (w^*)^4 & (w^*)^6 \\
1 & (w^*)^3 & (w^*)^6 & (w^*)^9 \\
}
\right)^T \\
& \eql &
\mat{
1 & 1 & 1 & 1 \\
1 & w^* & (w^*)^2 & (w^*)^3 \\
1 & (w^*)^2 & (w^*)^4 & (w^*)^6 \\
1 & (w^*)^3 & (w^*)^6 & (w^*)^9 \\
}
}$$
- Finally, let's work through \(D^\dagger D\):
$$\eqb{
D^\dagger D
& \eql &
\mat{
1 & 1 & 1 & 1 \\
1 & w^* & (w^*)^2 & (w^*)^3 \\
1 & (w^*)^2 & (w^*)^4 & (w^*)^6 \\
1 & (w^*)^3 & (w^*)^6 & (w^*)^9 \\
}
\mat{
1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 \\
1 & w^2 & w^4 & w^6 \\
1 & w^3 & w^6 & w^9 \\
}\\
& \eql &
\mat{
N & 0 & 0 & 0\\
0 & N & 0 & 0\\
0 & 0 & N & 0\\
0 & 0 & 0 & N\\
} \\
& \eql &
N \mat{
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
} \\
& \eql & N I
}$$
Observe why the product of the i-th row of \(D^\dagger\) and the i-th
column of \(D\) is \(N\), for example with \(i=2\):
$$\eqb{
& &
\mbox{row \(2\) of \(D^\dagger\) \(\times\) column \(2\) of \(D\)}\\
& \eql &
1 + w^*w + (w^*)^2w^2 + (w^*)^3w^3 \\
& \eql &
1 + |w|^2 + |w^2|^2 + |w^3|^2 \\
& \eql &
N
}$$
(where \(N=4\) in this example)
- Finally, we see that
$$
D^{-1} \eql \frac{1}{N} D^\dagger
$$
because then
$$
D^{-1} D \eql \frac{1}{N} D^\dagger D \eql I
$$
We'll now consider an unusual kind of input vector:
- Now consider an integer \(r\) that divides \(N\) and let
\(m = \frac{N}{r}\) be the quotient.
- For example, consider \(N=8, r=2, m=4\).
- We'll create a vector \(v\) with \(m\) \(1\)'s that are equally
spaced, perhaps with some offset (from the first position),
and multiply by \(D\):
$$
Dv
\eql
\mat{
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & w & w^2 & w^3 & w^4 & w^5 & w^6 & w^7\\
1 & w^2 & w^4 & w^6 & w^8 & w^{10} & w^{12} & w^{14}\\
1 & w^3 & w^6 & w^9 & w^{12} & w^{15} & w^{18} & w^{21}\\
1 & w^4 & w^8 & w^{12} & w^{16} & w^{20} & w^{24} & w^{28}\\
1 & w^5 & w^{10} & w^{15} & w^{20} & w^{25} & w^{30} & w^{35}\\
1 & w^6 & w^{12} & w^{18} & w^{24} & w^{30} & w^{36} & w^{42}\\
1 & w^7 & w^{14} & w^{21} & w^{28} & w^{35} & w^{42} & w^{49}\\
}
\mat{0\\ 1\\ 0\\ 1\\ 0\\ 1\\ 0\\ 1\\}
$$
The \(1\)'s are spaced every \(r=2\) spots in the vector.
- Consider the third row times the vector:
$$\eqb{
w^2 + w^6 + w^{10} + w^{14}
& \eql &
w^2( 1 + w^4 + (w^4)^2 + (w^4)^3) \\
& \eql &
w^2 \frac{1 - (w^4)^4}{1 - w^4} \\
& \eql &
w^2 \frac{1 - (w^8)^2}{1 - w^4} \\
& \eql &
w^2 \frac{1 - (1)^2}{1 - w^4} \\
& \eql &
0
}$$
- This too is similar to a subset of equally spaced arrows.
- However, consider the 5th row:
$$\eqb{
w^4 + w^{12} + w^{20} + w^{28}
& \eql &
w^4( 1 + w^{8} + (w^8)^2 + (w^8)^3) \\
& \eql &
w^4( 1 + 1 + 1 + 1) \\
& \; \neq \; & 0
}$$
- The pattern here is that the \(p\)-th row looks like
$$
(w^p)^1 + (w^p)^{1+r} + (w^p)^{1+2r} + \ldots
$$
(skipping by \(r\) because that's the spacing of \(1\)'s in the vector).
- This becomes
$$
(w^p) \parenl{ (w^p)^{r} + (w^p)^{2r} + \ldots }
$$
which is non-zero when \(pr\) is a multiple of \(N\).
- There are \(\frac{N}{r} = m\) rows for which this occurs.
- Thus, the product vector in this case will look like
$$
\mat{ \mbox{nonzero} \\ 0\\ 0\\ 0\\ \mbox{nonzero} \\ 0 \\ 0 \\ 0}
$$
These non-zero numbers are spaced \(m=4\) apart.
- Thus, the \(r\)-spaced non-zero numbers in \(v\) become
\(m\)-spaced numbers in the result vector.
- We are now glimpsing how this matrix "recognizes"
periodicity:
- A periodicity of \(r\) in the input turns into \(m =
\frac{N}{r}\) periodicity in the output.
- This, just by multiplication.
- Note: the assumption here is \(r\) divides \(N\) cleanly:
\(N \md r = 0\).
D.3
The DFT and some DFT conventions
Let's start by writing out the input, output and \(D\) symbolically:
- We'll write
$$
\tilde{v} \eql D v
$$
- Expanding, we'll write the components as:
$$
\mat{ \tilde{a}_0 \\ \tilde{a}_1 \\ \tilde{a}_2\\ \vdots \\ \tilde{a}_{N-1} }
\eql
\mat{
1 & 1 & 1 & \ldots & 1 \\
(w)^0 & w & w^2 & \ldots & w^{N-1} \\
(w^2)^0 & w^2 & w^4 & \ldots & w^{2(N-1)} \\
(w^3)^0 & w^3 & w^6 & \ldots & w^{3(N-1)} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
(w^k)^0 & w^k & (w^k)^2 & \ldots & w^{k(N-1)} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
(w^{N-1})^0 & w^{N-1} & w^{2(N-1)} & \ldots & w^{(N-1)(N-1)}
}
\mat{ a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1} }
$$
Note: the first column is all \(1\)'s.
- Observe that
$$\eqb{
\tilde{a}_j & \eql & \sum_{k=0}^{N-1} (w^{j})^{k} a_k \\
& \eql & \sum_{k=0}^{N-1} a_k w^{jk} \\
}$$
- Thus, we will think of \(D\) as a matrix that
transforms a vector \(v=(a_0,\ldots,a_{N-1})\) to
a vector \(\tilde{v}=(\tilde{a}_0,\ldots,\tilde{a}_{N-1})\):
$$
\tilde{v} \eql D v
$$
- Think of \(v\) as a vector of data (sometimes called
the signal).
- The output, \(\tilde{v}\), is commonly called the spectrum.
- Each \(\tilde{a}_j\) is called a Fourier coefficient.
- Note that because \(D\) is invertible, we can recover
the input from the output:
$$
v \eql D^{-1} \tilde{v}
\eql \frac{1}{N} D^\dagger \tilde{v}
$$
- Now, because \(D^\dagger\) is a matrix with the same
qualitative properties, we could potentially feed data into it:
$$
\bar{v} \eql D^\dagger v
$$
We would not get \(\tilde{v}\) exactly, but something with similar properties.
- Again, we'd call \(\bar{v}\) the spectrum.
The two conventions:
- The convention in signal processing is to use \(D^\dagger\) to
transform the input:
$$
\bar{v} \eql D^\dagger v
$$
where
$$
D^\dagger \eql \mbox{the Discrete Fourier Transform}
$$
with the inverse defined as
$$
(D^\dagger)^{-1} \eql \frac{1}{N} D
\eql
\mbox{Inverse DFT}
$$
- Why then did we first start with \(D\)?
- It was simpler to introduce \(w\) first.
- The convention in quantum computing is to use
a variation of \(D\) as the DFT.
\(\rhd\)
We'll see this below.
D.4
The unitary DFT and the QFT
A unitary version of the pair \(D, D^\dagger\):
- Because \(D^\dagger D = NI \neq I\), the matrix \(D\) is not unitary.
- This is rather simple to fix. Define
$$
U_{\smb{DFT}} \eql \smf{1}{\sqrt{N}} D \\
$$
Then
$$
U^\dagger_{\smb{DFT}} \eql \smf{1}{\sqrt{N}} D^\dagger
$$
- Next,
$$
U^\dagger_{\smb{DFT}} U_{\smb{DFT}}
\eql
\smf{1}{\sqrt{N}} D^\dagger \smf{1}{\sqrt{N}} D
\eql I
$$
Thus, \(U^\dagger_{\smb{DFT}}\) is the inverse.
- And so, with input \(v=(a_0,\ldots,a_{N-1})\)
and output \(\tilde{v}=(\tilde{a}_0,\ldots,\tilde{a}_{N-1})\):
$$\eqb{
\tilde{v} & \eql & U_{\smb{DFT}} v \\
v & \eql & U^\dagger_{\smb{DFT}} \tilde{v} \\
}$$
The elements of \(\tilde{v}\) are now scaled by \(\frac{1}{\sqrt{N}}\).
We will write both directions using summations because that
will turn out to be useful in algorithms:
-
The j-th element of \(\tilde{v}\) comes from the j-th row of
\(U_{\smb{DFT}}\):
$$\eqb{
\tilde{a}_j
& \eql & \smf{1}{\sqrt{N}} \sum_{k=0}^{N-1} a_k w^{jk} \\
& \eql & \smf{1}{\sqrt{N}}
\sum_{k=0}^{N-1} a_k e^{\frac{2\pi jki}{N}} \\
}$$
where we've expanded \(w\) to see this written directly
in terms of the complex exponentials.
- The reverse direction:
$$\eqb{
{a}_j
& \eql & \smf{1}{\sqrt{N}} \sum_{k=0}^{N-1} \tilde{a}_k w^{-jk} \\
& \eql & \smf{1}{\sqrt{N}}
\sum_{k=0}^{N-1} \tilde{a}_k e^{\frac{-2\pi jki}{N}} \\
}$$
Let's now use Dirac notation:
- We will henceforth assume \(N\) is a power of \(2\): \(N = 2^n\).
(This was not necessary for standard DFT, but is also commonly
assumed there.)
- The vector \(v=(a_0,\ldots,a_{N-1})\) can be written as
$$\eqb{
\kt{v}
& \eql &
\mat{a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1}} \\
& \eql &
a_0 \mat{1 \\ 0 \\ 0 \\ \vdots \\ 0}
+
a_1 \mat{0 \\ 1 \\ 0 \\ \vdots \\ 0}
+
a_2 \mat{0 \\ 0 \\ 1 \\ \vdots \\ 0}
+ \ldots +
a_{N-1} \mat{0 \\ 0 \\ 0 \\ \vdots \\ 1} \\
& \eql &
\sum_{x=0}^{N-1} a_x \kt{x}
}$$
- Similarly,
\(\tilde{v}=(\tilde{a}_0,\ldots,\tilde{a}_{N-1})\)
can be written as
$$
\kt{\tilde{v}}
\eql
\sum_{y=0}^{N-1} \tilde{a}_y \kt{y}
$$
- Since
$$
\tilde{a}_y \eql \smf{1}{\sqrt{N}} \sum_{x=0}^{N-1} a_x w^{xy}
$$
we can substitute for \(\tilde{a}_y\) above:
$$\eqb{
\kt{\tilde{v}}
& \eql &
\sum_{y=0}^{N-1} \tilde{a}_y \kt{y} \\
& \eql &
\sum_{y=0}^{N-1}
\left( \smf{1}{\sqrt{N}} \sum_{x=0}^{N-1} a_x w^{xy} \right)
\; \kt{y} \\
& \eql &
\smf{1}{\sqrt{N}} \sum_{y=0}^{N-1} \sum_{x=0}^{N-1}
a_x w^{xy} \kt{y}
}$$
- We can summarize this as:
$$
\kt{\tilde{v}}
\eql U_{\smb{DFT}} \kt{v}
\eql
\smf{1}{\sqrt{N}} \sum_{y=0}^{N-1} \sum_{x=0}^{N-1}
a_x w^{xy} \kt{y}
$$
Note:
- The outer sum is over standard-basis vectors \(\kt{y}\).
- The inner sum is over numbers.
- Why is this useful?
- By creating an expression using standard-basis vectors,
we get get Dirac-algebra to work for us in the quantum-circuit context.
- The unitary matrix \(U_{\smb{DFT}}\), when implemented
as a quantum-circuit unitary, is the Quantum Fourier
Transform, and so we'll write this as:
$$
\kt{\tilde{v}}
\eql U_{\smb{QFT}} \kt{v}
$$
- Finally, note that \(\kt{v}=(a_0,\ldots,a_N)\) above is any
vector. Let's see what the QFT does to a standard-basis vector:
- Consider a particular integer \(x\)
with \(a_x=1\) with all other \(a_k=0\).
- This makes \(\kt{v}=\kt{x}\). (Do you see why?)
- Then the QFT results in:
$$
U_{\smb{QFT}} \kt{x}
\eql
\smf{1}{\sqrt{N}} \sum_{y=0}^{N-1} w^{xy} \kt{y}
$$
D.5
What is the DFT used for?
The primary use of the DFT can be described
as extracting and manipulating periodicity:
- Let's use audio as an example.
- Think of digitized sound as a sequence of numbers:
- Each number might represent "intensity" of audio signal, for example.
- Applying the DFT produces a spectrum that captures
information about what audio frequencies are present and to what degree:
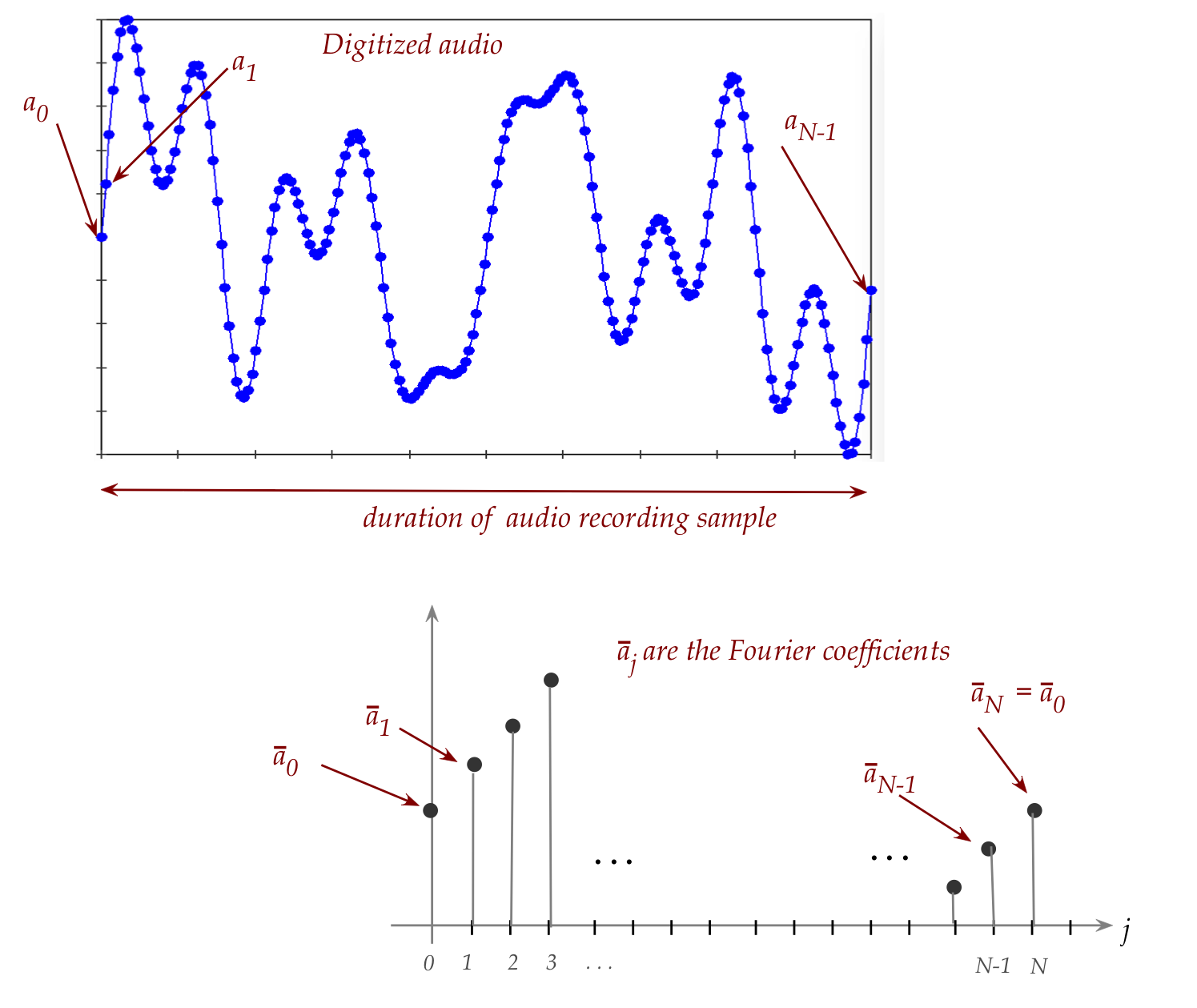
- The periodicity in this case comes from audio that's composed
of periodic (sine) waves.
- Each resulting \(\tilde{a}_j\) describes the strength,
loosely speaking, of the the j-th frequency in the signal.
- Beyond analysis, the spectrum can be modified and
reconverted into modified audio.
- Thus, high frequencies can be removed altogether by making
some \(\tilde{a}_j=0\).
- This is what happens with noise removal.
- In addition, one can boost bass/treble by increasing
corresponding \(\tilde{a}_j\)'s.
- There's much more to signal analysis and modification
\(\rhd\)
This is an entire field by itself: signal processing
The Fast Fourier Transform (FFT):
- The multiplication of an \(N\times N\) matrix into an
\(N\)-sized vector takes \(N^2\) time:
- Each row times the input vector requires \(N\) multiplications,
and \(N\) additions (to accumulate the sum).
- For large data (millions of numbers in a vector), an \(N^2\)
calculation can be slow.
- The Fast Fourier Transform (FFT) is a way to calculate the
DFT using \(N\log N\) arithmetic operations, a significant improvement.
D.6*
The Fourier basis
Let's take another look at the numbers in the spectrum,
\(\tilde{v}=(\tilde{a}_0,\ldots,\tilde{a}_{N-1})\),
and ask: are these coordinates in some basis?
Indeed they are ... coordinates in the Fourier basis:
- First, let's go back to:
$$
\kt{\tilde{v}} \eql U_{\smb{DFT}} \kt{v}
$$
and expand to write
$$
\mat{ \tilde{a}_0 \\ \tilde{a}_1 \\ \tilde{a}_2\\ \vdots \\ \tilde{a}_{N-1} }
\eql
\mat{
\frootn{1} & \frootn{1} & \frootn{1} & \ldots & \frootn{1} \\
\frootn{1} & \frootn{w} & \frootn{w^2} & \ldots & \frootn{w^{N-1}} \\
\frootn{1} & \frootn{w^2} & \frootn{w^4} & \ldots & \frootn{w^{2(N-1)}} \\
\frootn{1} & \frootn{w^3} & \frootn{w^6} & \ldots & \frootn{w^{3(N-1)}} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\frootn{1} & \frootn{w^k} & \frootn{(w^k)^2} & \ldots & \frootn{w^{k(N-1)}} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\frootn{1} & \frootn{w^{N-1}} & \frootn{w^{2(N-1)}} & \ldots & \frootn{w^{(N-1)(N-1)}}
}
\mat{ a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1} }
$$
- And write the inverse in the same way:
$$
\kt{v} \eql U^\dagger_{\smb{DFT}} \kt{\tilde{v}}
$$
Which becomes
$$
\mat{ a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1} }
\eql
\mat{
\frootn{1} & \frootn{1} & \frootn{1} & \ldots & \frootn{1} \\
\frootn{1} & \frootn{w^*} & \frootn{(w^*)^2} & \ldots & \frootn{(w*)^{N-1}} \\
\frootn{1} & \frootn{(w^*)^2} & \frootn{(w^*)^4} & \ldots & \frootn{(w^*)^{2(N-1)}} \\
\frootn{1} & \frootn{(w^*)^3} & \frootn{(w^*)^6} & \ldots & \frootn{(w^*)^{3(N-1)}} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\frootn{1} & \frootn{(w^*)^k} & \frootn{(w^*)^{2k}} & \ldots & \frootn{(w^*)^{k(N-1)}} \\
\vdots & \vdots & \vdots & \vdots & \vdots \\
\frootn{1} & \frootn{(w^*)^{N-1}} & \frootn{(w^*)^{2(N-1)}} & \ldots & \frootn{(w^*)^{(N-1)(N-1)}}
}
\mat{ \tilde{a}_0 \\ \tilde{a}_1 \\ \tilde{a}_2\\ \vdots \\ \tilde{a}_{N-1} }
$$
- Suppose we name the columns in the above matrix as:
$$
\mat{ a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{N-1} }
\eql
\mat{
\vdots & \vdots & \vdots & \vdots \\
f_0 & f_1 & \ldots & f_{N-1} \\
\vdots & \vdots & \vdots & \vdots \\
}
\mat{ \tilde{a}_0 \\ \tilde{a}_1 \\ \tilde{a}_2\\ \vdots \\ \tilde{a}_{N-1} }
$$
- Then,
$$
\kt{v} \eql \tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}}
$$
- We've now expressed the data \(\kt{v}\) in the Fourier basis
as a linear combination of the vectors in that basis.
- To summarize, there are two expressions of the data:
- Expression in the standard basis:
$$
\kt{v} \eql
\mat{{a}_0\\ {a}_1\\ \vdots\\ {a}_{N-1}}
\eql
{a}_0
\mat{1\\ 0\\ \vdots\\ 0}
\; + \;
{a}_1
\mat{0\\ 1\\ \vdots\\ 0}
\; + \;
\ldots
\; + \;
{a}_{N-1}
\mat{0\\ 0\\ \vdots\\ 1}
$$
Here, the coefficients are the signal.
- And the same data in the Fourier basis:
$$\eqb{
\kt{v} & \eql &
\tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}} \\
& \eql &
\tilde{a}_0 \mat{1 \\ 1 \\ \vdots \\ 1}
+ \tilde{a}_1 \mat{1\\ \frootn{w^*} \\ \vdots \\ \frootn{(w^*)^{N-1}}}
+ \ldots
+ \tilde{a}_{N-1} \mat{1\\ \frootn{(w*)^{N-1}} \\ \vdots \\
\frootn{(w^*)^{(N-1)(N-1)}} }
}$$
In this case, the coefficients are called the spectrum.
- Let's now take this a step further, and look closely
at which basis we use for "numerifying".
- Consider the expression
$$
\kt{v} \eql
\tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}}
$$
This is abstract, with no "numerification".
- If we numerify in the standard basis, we'll write
$$
\kt{v} \eql
\tilde{a}_0 \mat{1 \\ 1 \\ \vdots \\ 1}
+ \tilde{a}_1 \mat{1\\ \frootn{w^*} \\ \vdots \\ \frootn{(w^*)^{N-1}}}
+ \ldots
+ \tilde{a}_{N-1} \mat{1\\ \frootn{(w*)^{N-1}} \\ \vdots \\
\frootn{(w^*)^{(N-1)(N-1)}} }
\eql
\mat{{a}_0\\ {a}_1\\ \vdots\\ {a}_{N-1}}
$$
- What would it look like if we numerify in the Fourier basis?
- Here, each Fourier basis vector numerified in its own basis
looks like:
$$
\kt{f_0} \eql \mat{1\\ 0\\ \vdots \\ 0}
\;\;\;\;\;\;
\kt{f_1} \eql \mat{0\\ 1\\ \vdots \\ 0}
\;\;\;\;\;\;
\kt{f_{N-1}} \eql \mat{0\\ 0\\ \vdots \\ 1}
$$
Why? Because, for example,
$$
\kt{f_1} \eql 0 \cdot \kt{f_0} + 1\cdot \kt{f_1} + \ldots + 0\cdot\kt{f_{N-1}}
\eql
\kt{f_1} \eql \mat{0\\ 1\\ \vdots \\ 0}
$$
- Thus, when numerified in the Fourier basis, the data looks like:
$$
\kt{v} \eql
\tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}}
\eql
\mat{ \tilde{a}_0 \\ \tilde{a}_1 \\ \tilde{a}_2\\ \vdots \\ \tilde{a}_{N-1} }
$$
- This should not be surprising because
we already knew from
$$
\kt{v} \eql
\tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}}
$$
that the Fourier coefficients are the coordinates in the Fourier basis.
Let's now express coefficients using inner products:
- Recall that we wrote
$$
\kt{v} \eql
\tilde{a}_0 \kt{f_0} + \tilde{a}_1 \kt{f_1}
+ \ldots + \tilde{a}_{N-1} \kt{f_{N_1}}
$$
- Those coefficients can be written as:
$$
\kt{v} \eql
\inr{f_0}{v} \kt{f_0} + \inr{f_1}{v} \kt{f_1}
+ \ldots + \inr{f_{N-1}}{v} \kt{f_{N_1}}
$$
That is,
$$
\tilde{a}_j \eql \inr{f_j}{v}
$$
- If we are to calculate this, we need to numerify
both \(\kt{f_j}\) and \(\kt{v}\) in the same basis.
- In the standard basis, this would be the calculation
$$
\inr{f_j}{v}
\eql
\mat{
\frootn{1} & \frootn{w^j} & \frootn{w^2j} & \ldots & \frootn{w^{j(N-1)}}}
\mat{{a}_0\\ {a}_1\\ \vdots\\ {a}_{N-1}}
$$
where we have the conjugate row form of \(\kt{f_j}\).
- Notice: \(\br{f_j}\) is the j-th row of \(U_{\smb{DFT}}\).
Finally, let's clarify these ideas with an example from real unit-length vectors, which will allow us to draw a picture:
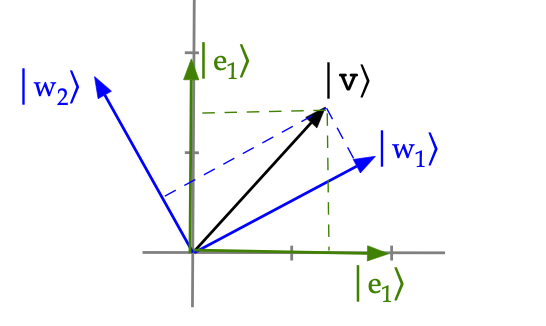
- Suppose we have a vector \(\kt{v}\) and two different bases:
- Basis 1: the standard basis (in green above) that we'll
call \(\kt{e_1}, \kt{e_2}\)
- Basis 2: \(\kt{w_1}, \kt{w_2}\) (in blue above),
- Abstractly, we can express \(\kt{v}\) in each basis as:
$$\eqb{
\kt{w} & \eql & \inr{e_1}{v} \kt{e_1} + \inr{e_2}{v} \kt{e_2}\\
\kt{w} & \eql & \inr{w_1}{v} \kt{v_1} + \inr{w_2}{v} \kt{v_2}\\
}$$
- Here, the coordinates in the standard basis are:
\(\inr{e_1}{v}, \inr{e_2}{v}\).
- And in the other basis: \(\inr{w_1}{v}, \inr{w_2}{v}\).
- Now, to make a calculation, we need to numerify.
- Suppose we perform calculations in the standard basis:
- Typically, we're given the coordinates of \(\kt{v}\)
as in:
$$
\kt{v} \eql \mat{\isqts{1}\\ \isqts{1}}
$$
- Then
$$\eqb{
\inr{e_1}{v} & \eql &
\mat{1 & 0} \mat{\isqts{1}\\ \isqts{1}} & \eql & \isqts{1}\\
\inr{e_2}{v} & \eql &
\mat{0 & 1} \mat{\isqts{1}\\ \isqts{1}} & \eql & \isqts{1}\\
}$$
where \(\kt{e_1}, \kt{e_2}\) are expressed in their own
basis.
- To calculate the coordinates in the other basis,
we need the numerification of \(\kt{w_1}, \kt{w_2}\)
- Again, this is typically given or known.
(How else would these be specified?)
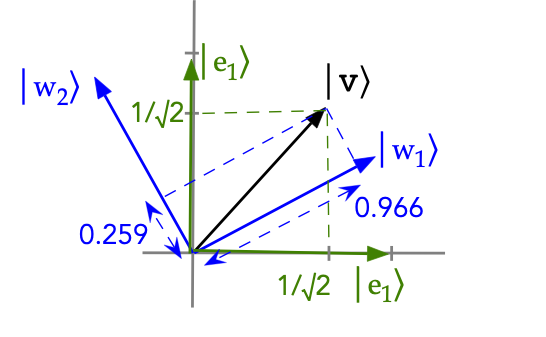
- Suppose we're given
$$\eqb{
\kt{w_1} & \eql & \mat{ \frac{\sqrt{3}}{2} \\ \frac{1}{2} } \\
\kt{w_2} & \eql & \mat{ -\frac{1}{2} \\ \frac{\sqrt{3}}{2} } \\
}$$
Then,
$$\eqb{
\inr{w_1}{v} & \eql &
\mat{ \frac{\sqrt{3}}{2} & \frac{1}{2} }
\mat{\isqts{1}\\ \isqts{1}}
& \eql & \smf{\sqrt{3}+1}{2\sqrt{2}} & \approx & 0.966\\
\inr{w_2}{v} & \eql &
\mat{ -\frac{1}{2} & \frac{\sqrt{3}}{2} }
\mat{\isqts{1}\\ \isqts{1}}
& \eql & \smf{\sqrt{3}-1}{2\sqrt{2}} & \approx & 0.259\\
}$$
-
Which is what we see in the diagram:
